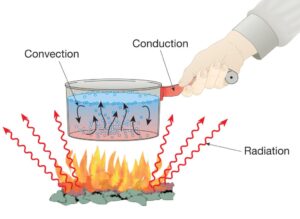
熱膨張とは、温度が上昇するにつれて物質の幾何学的寸法(長さ、面積、体積)が増加することです。冷却によるこのプロセスの逆転は、しばしば熱収縮と呼ばれます。この挙動を表す特徴的な値が熱膨張係数で、長さや体積の変化を温度の変化で割った値で表されます。
材料を加熱すると粒子の動きが速くなり、粒子間の分子間力が弱まります。その結果、原子や分子間の平均分離が大きくなり、巨視的なレベルでは幾何学的寸法の拡大や材料の密度の低下として現れます。しかし、限られた温度範囲内では、温度の上昇に伴って収縮する材料もあります。このような挙動は例外的ですが、0 °Cから4 °Cの間の水のように、一般的に知られている例もあります。
熱膨張の応用と例
熱膨張の日常的な例としては、水銀、アルコール、ガラス入り液体温度計などがあります。温度が上昇すると、液体が膨張して温度計の毛細管を上昇します。もう1つの一般的な例は熱気球で、膨張する熱気の低密度が上向きの力を発揮して熱気球を浮かせます。
しかし、熱膨張は多くの工学的用途においてしばしば危険をもたらします。例えば、密閉された油圧システムや給湯システムでは、熱膨張タンクは、最低温度と最高温度の間の作動油の体積変化を吸収し、圧力をほぼ一定に保つために必要な部品です。
同様に、固体の熱膨張は、特に建設業では重大な危険となります。鉄道の線路は、太陽によって加熱されると、熱膨張による圧縮応力によって座屈することがあります。いわゆる「サンキンク」と呼ばれるこの現象は図1に示されており、列車の脱線を引き起こす可能性があります。

高温時の建物、パイプライン、道路、橋梁にも同様の影響があります。図2の橋のように、伸縮継手は熱膨張に対応し、損傷や座屈を防ぎます。

そのため、熱伝導や高温を伴う工学的な取り組みにおいては、熱膨張について十分に理解しておく必要があります。
熱膨張の数学的説明
温度の変化は、固体や液体の体積の変化につながります。この現象を定量化するために、材料と温度に依存する熱膨張係数を次のように定義します。
$$\gamma = \frac{1}{V_0} \left (\frac{\partial V}{\partial T} \right )_\mathrm{p}\tag{1}$$
温度の変化が小さい場合、相対体積の変化\(\frac{\Delta V}{V_0} = \frac{V-V_0}{V_0}\) と温度の変化\(\Delta T = T – T_0\) はほぼ直線的な関係にあり、平均熱膨張係数を定義することができます:
$$ \bar \gamma = \frac{\Delta V}{(V_0)(\Delta T)}\tag{2}$$
体積膨張係数、面 積膨張係数、線形膨張係数の3種類が開発されています。固体では、問題を単純化して、体積の変化ではなく一次元の変化を考慮する線形膨張にすることができます。この場合、長さの変化は線形熱膨張係数によって温度変化に関連付けられます:
$$ \alpha = \frac{1}{L_0} \left (\frac{\partial L}{\partial T} \right )_\mathrm{p} , \bar \alpha = \frac{\Delta L}{L_0 \Delta T}\tag{3}$$
線膨張係数が温度によってあまり変化せず、長さの変化が小さい限り、線膨張係数の平均値の推定はうまくいきます\(\frac{\Delta L}{L} \text{«} 1\) 。ほとんどの場合、固体は係数の温度依存性をほとんど示しません。\(\bar \gamma = 3 \bar \alpha\)等方性材料の場合、体積熱膨張は線形係数の3倍です。この係数はほとんど常に正の値です。まれに温度上昇に伴って材料が収縮する場合、係数は負になります。
様々な材料の線熱膨張係数の値
様々な材料の線膨張係数の値
表1 に一般的な工学材料の線熱膨張係数を示します。
| 材料名 | 線膨張係数 [\(10^{-6} ℃\)] |
|---|---|
| ABS | 80 |
| アルミニウム | 23 |
| 真鍮 | 17-21 |
| セラミック (ZrO2) | 10.5 |
| コンクリート | 10 |
| 銅 | 16.5 |
| コルク | 40 |
| エポキシ | 50 |
| FR4 | 14 |
| ガラス | 9 |
| ホウケイ酸ガラス | 3.3 |
| 金 | 14 |
| 花崗岩 | 4.4 |
| 氷 | 28 |
| インバー | 0.6-2.1 |
| 鉄 | 11.8 |
| 延性高クロム鋳鉄 | 9.3-9.9 |
| 鉄-コバルト-ニッケル合金 | 0.6-8.7 |
| 磁性軟鉄合金 | 2.0-12 |
| 鉛 | 28 |
| マグネシウム | 25 |
| ニッケル | 13.4 |
| プラチナ | 8.8-9.1 |
| PA6 (ナイロン6) | 91 |
| PA6 GF30 | 20-30 |
| PA66 GF30 (ナイロン66) | 20-30 |
| ポリエチレン(HDPE) | 169 |
| ポリプロピレン(PP) | 194 |
| ポリオキシメチレン(POM) | 95 |
| ポリメタクリル酸メチル(PMMA) | 69 |
| ポリスチレン(PS) | 71 |
| ポリテトラフルオロエチレン(PTFE) | 119 |
| ポリ塩化ビニル(PVC) (at 50 °C) | 75 |
| ゴム | 6.7 |
| シリコン | 2.6-3.3 |
| 銀 | 19 |
| ステンレス銅 | 9.3-25 |
| スチール | 8.6-19 |
| 構造用鋼 | 12 |
| チタン | 8.5 |
| 非合金チタン/ 低合金チタン | 7.6-9.9 |
| タングステン | 4.5 |
熱応力 (温度応力) 解析
構造物の熱応力は、物理的制約のある固体の温度が一様に上昇する場合に発生します。両端が固定された梁に一様な温度上昇が生じると、\(\sigma = E \epsilon_T – \alpha E \Delta T\) に等しい圧縮応力が発生します。これは、次のような状況の重ね合わせによって導かれます:

不均一な温度分布も熱応力を誘発し、材料内の不均一な熱膨張を引き起こします。一般的な熱力学のケースでは、部分的な力学的制約と不均一な温度分布が組み合わされた固体が扱われます。この場合の温度分布は次のように表されます:
$$ \frac{\partial}{\partial x} \left (k \frac{\partial T(x,y,z,t)}{\partial x} \right ) + \frac{\partial}{\partial y} \left (k \frac{\partial T(x,y,z,t)}{\partial y} \right ) + \frac{\partial}{\partial z} \left (k \frac{\partial T(x,y,z,t)}{\partial z} \right ) + Q(x,y,z,t) = \rho c \frac{\partial T(x,y,z,t)}{\partial t}\tag{4}$$
上式の解法は、図 4 に示す固体の熱応力解析に先立つ必要なステップです。熱応力有限要素解析の最初のステップは、熱流方程式を解いて温度場を計算することです。その後、この温度場を体積力に相当するものとして応力解析を行います。
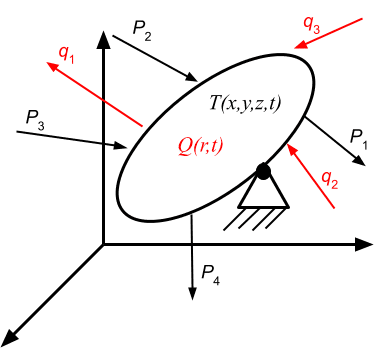
図 4 は、熱流束\(q_1, q_2, q_3, … \) とQで表される熱源またはシンクによって生成される温度場分布 T(x, y, z, t) を持つ固体を示しています。この固体には機械的な力\(P_1, P_2, P_3, P_4, … \) も作用します。固体を有限要素に離散化すると、要素のひずみは次のように記述できます:
$$\begin{Bmatrix}\epsilon\end{Bmatrix} = \begin{Bmatrix}\epsilon _\mathrm{M}\end{Bmatrix} + \begin{Bmatrix}\epsilon _\mathrm{T}\end{Bmatrix}\tag{5}$$
\(\begin{Bmatrix}\epsilon _\mathrm{M}\end{Bmatrix}\) は機械的な力と応力によって生じるひずみです:
$$\begin{Bmatrix}\epsilon _\mathrm{M}\end{Bmatrix} = \begin{bmatrix}D\end{bmatrix}^{-1}\begin{Bmatrix}\sigma\end{Bmatrix}\tag{6}$$
\(\begin{bmatrix}D\end{bmatrix}^{-1}\) \(\begin{Bmatrix}\epsilon _\mathrm{T}\end{Bmatrix}\) は熱流束と熱源による温度変化によって誘発されるひずみ:
\(\begin{Bmatrix}\epsilon _\mathrm{T}\end{Bmatrix} =
\begin{pmatrix}
\epsilon _\mathrm{T,xx} \\
\epsilon _\mathrm{T,yy} \\
\epsilon _\mathrm{T,zz} \\
\end{pmatrix} =
\begin{pmatrix}
\alpha \Delta T \\
\alpha \Delta T \\
\alpha \Delta T \\
\end{pmatrix}\tag{7} \)
情報源[1-3]に詳述されているように、少し計算をすると、よく知られた要素方程式にたどり着きます:
$$\begin{bmatrix}K_\mathrm{e}\end{bmatrix} \begin{Bmatrix}\Phi\end{Bmatrix} = \begin{Bmatrix}f_\mathrm{M}\end{Bmatrix} + \begin{Bmatrix}f_\mathrm{T}\end{Bmatrix} \tag{8}$$
このように、熱膨張は有限要素法 (FEA) に組み込まれています。
SimScaleにおける熱応力 (温度応力) 解析
SimScaleのThermomechanicalソルバーは、構造荷重と熱膨張の影響を連成します。これにより、構造物の挙動を仮想的に試験・予測し、静的および熱荷重条件下における複雑な構造工学上の問題を解決できます。FEAシミュレーションプラットフォームは、スケーラブルな数値解析手法を採用しており、複雑な荷重、形状、または材料特性のために通常は計算が非常に困難な数式も計算できます。
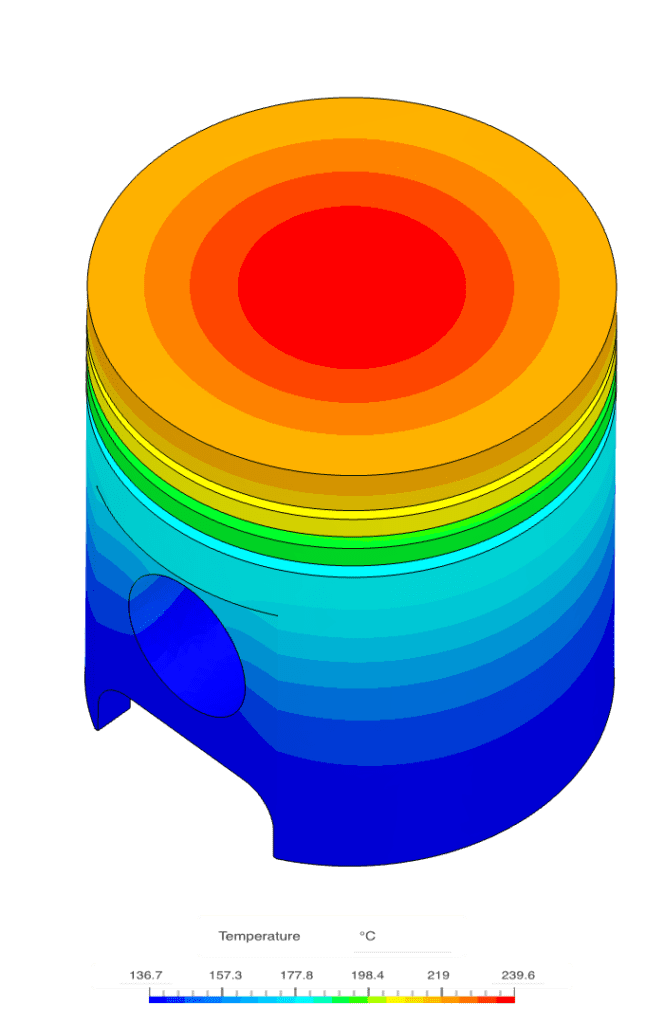
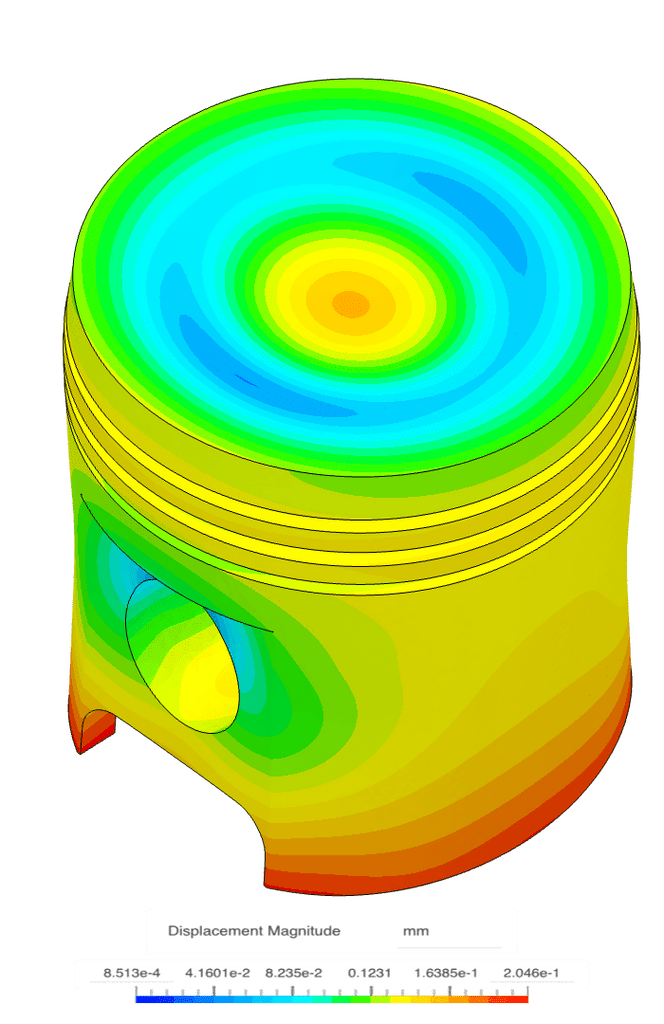
左側は温度場、中央は応力分布です。特にピストンヘッド上部において、応力と温度勾配の相関関係が確認できます。右側は変形 (20倍スケール)です。これらのシミュレーションは非常に簡単に設定でき、誰でも複数のシミュレーションを並行して実行して、すぐに有用な結果を生成できます。

参考文献:
- Logan, Daryl, A First Course in the Finite Element Method, Chapter 15: Thermal Stress, Cengage Learning, 2012.
- Hsu, Tai-Ran, The Finite Element Method in Thermomechanics, Chapter 3: Thermoelastic-plastic Stress Analysis, Allen and Unwin, 1986.
- Hsu, Tai-Ran, Lecture Notes on Thermal Stress Analysis of Solid Structures Using Finite Element Method, Introduction to Finite Element Method, San Jose University, 2017.
- ASM Ready Reference: Thermal Properties of Metals, Chapter 2: Thermal Expansion, ASM International, 2002.
- VDI Heat Atlas, Chapter D6: Properties of Solids and Solid Materials, Springer, 2010.
熱膨張と合わせて読みたい
SimScale製品紹介資料ダウンロード

資料請求
資料全体をご希望の方はこちらのフォームからお申し込みください。