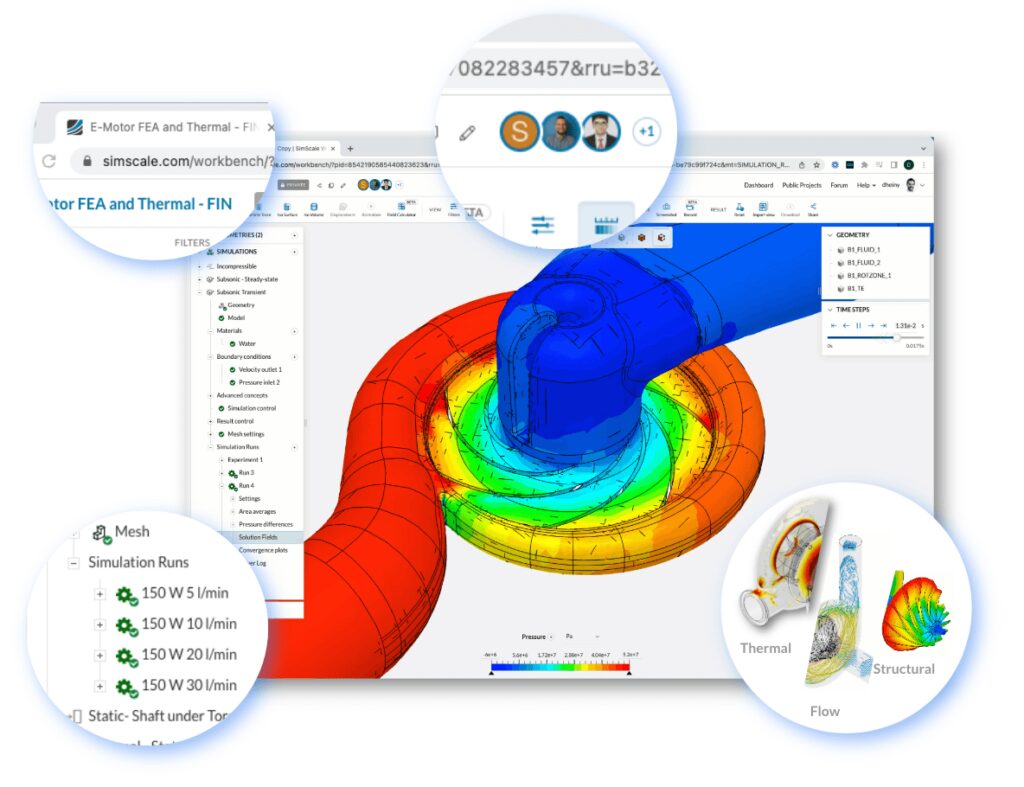
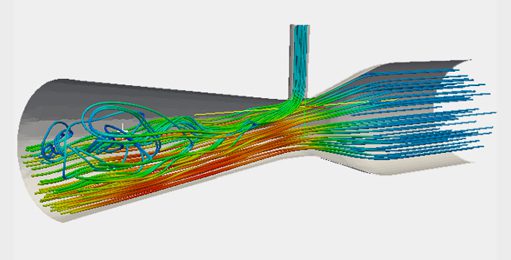
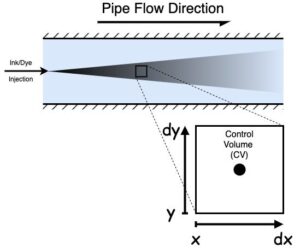
ナビエ・ストークス（Navier-Stokes/NS）方程式は、流体の運動を支配する偏微分方程式です。この方程式は流体力学の基本方程式です。

物理領域における流体の運動は、様々な特性によって決定します。流体の挙動を明らかにするためには、これらの特性を正確に定義する必要があります。

速度、圧力、温度、密度、粘性は、流体の流れを調べる際に考慮すべき主な特性です。燃焼、混相流、乱流、物質輸送などの物理現象に従って、これらの特性は非常に多様化し、運動学的特性、輸送特性、熱力学的特性、およびその他の特性に分類することができます$^1$ 。

熱流体は、保存の法則に基づく支配方程式によって定義されます。ナビエ・ストークス方程式は、動的および/または熱的相互作用中のこれらの特性の変化を調べるために広く適用される数学モデルを構成します。方程式は問題の内容に応じて調整可能で、質量、運動量、エネルギー保存の原則に基づいて表現されます$^1$ :

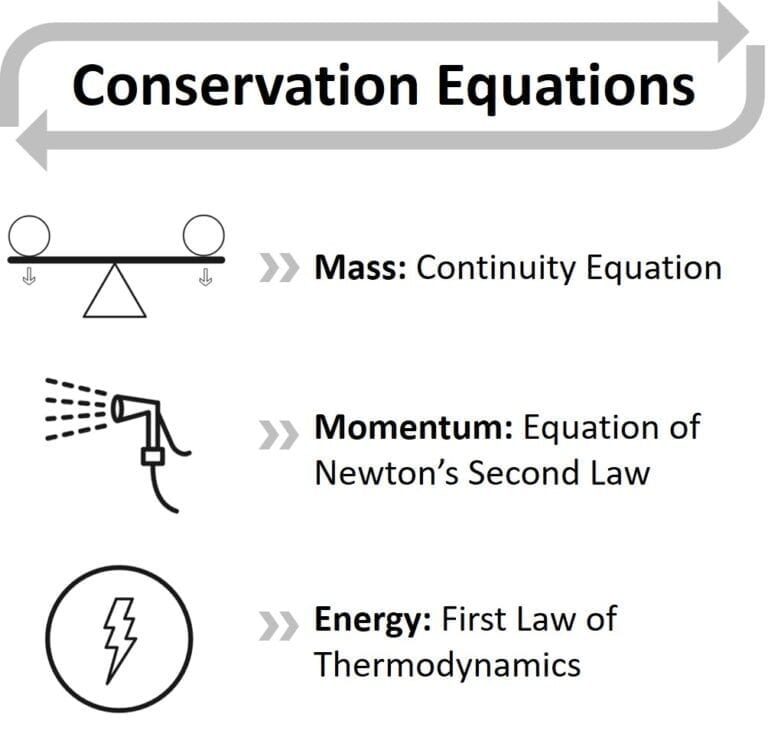
質量保存
連続の式
運動量保存
ニュートンの第二法則
エネルギー保存
熱力学第一法則またはエネルギー方程式

ナビエ・ストークス方程式は運動量保存のためだけの式としているものもありますが、物性保存のための方程式をすべて用いているものもあります。流体条件に関しては、ナビエ・ストークス方程式は、問題の複雑さが増加する場合に解を提供するためモデルが追加されることがあります。例えば、事前に計算されたレイノルズ数に従って乱流となる場合には、信頼できる結果を得るために適切な乱流モデルを適用する必要があります。

図1: 質量、運動量、エネルギーの保存方程式は、流体の流れをモデル化するために必要な支配方程式です。

ナビエ・ストークス方程式の歴史

流体の運動は人類にとって探求的なテーマであるにもかかわらず、数理モデルの進化は産業革命後の19世紀末と近代に現れました。粘性流体運動の最初の適切な記述は、アイザック・ニュートン卿による論文「プリンキピア」(1687)で示され、そこでは一定の粘性下での流体の動的挙動が研究されています$^1$ 。

その後、Daniel Bernoulli (1738)とLeonhard Euler (1755)が粘性流体の方程式を導きました。Claude-Louis Navier (1827)、Augustin-Louis Cauchy (1828)、Siméon Denis Poisson (1829)、Adhémar St.Venant(1843)らは、流体の流れの数理モデルを探求する研究を行っていましたが、粘性力(摩擦力)を見落としていました。

$^{1,2}$1845年、ジョージ・ストークス卿がニュートン流の粘性項を追加して粘性流の運動方程式を導き、ナビエ・ストークス方程式が完成しました。

つまり、ナビエ・ストークス方程式は、19世紀の数十年の間に、Claude-Louis NavierとSir George Stokesによって、それぞれ独立に徐々に導き出されたものです。この方程式は、ニュートンの運動第二法則を流体の流れに適用し、粘性流体の流れを記述するために粘性と圧力の効果を考慮したものです。

図2: 左からニュートン$^{9}$ 、ナビエ$^{10}$ 、ストークス$^{11}$ 、ナビエ・ストークス方程式を支えた数学者たち。

流体運動のラグランジュ表現とオイラー表現

運動学的特性に基づく流体の流れの観察方法は、便利な数学モデルを作成するための基本的な問題です。流体の運動は、ラグランジュ法またはオイラー法$^3$ のいずれかで調べることができます。

流体運動のラグランジュ表現は、流体粒子を監視することに基づいています。

時間$t_0$ の初期座標と時間$t_1$ の同じ粒子の座標の間には、ほとんど不可能な経路を通って何百万もの別々の粒子を調べなければなりません。

その代わりに、時間と位置の関数としての速度場を調べます。

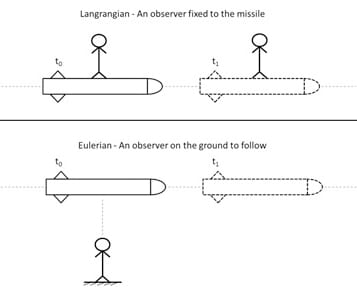
図3: ラグランジュ法とオイラー法による流体運動の観察。ラグランジアン法では、人はミサイルに対して安定していますが、オイラー法ではそうではありません。

運動のラグランジュ定式化は常に時間に依存します。$a$ 、$b$ 、$c$ は粒子の初期座標で、$x$ 、$y$ 、$z$ は時間$t$ における同じ粒子の座標です。ラグランジュ法の説明：

$$ x=x(a,b,c,t),y=y(a,b,c,t),z=z(a,b,c,t) \tag1$$

オイラー法では、$u$ 、$v$ 、$w$ は点$(x,y,z)$ における速度の成分で、$t$ は時間です。速度成分$u$ 、$v$ 、$w$ は未知数で、独立変数$x$ 、$y$ 、$z$ 、$t$ の関数です。$t$ の特定の値に対するオイラー法による運動の記述は次のようになります：

$$ u=u(x,y,z,t),v=v(x,y,z,t),w=w(x,y,z,t) \tag2$$

流体運動が記述されるオイラー系の保存方程式は、質量の連続方程式、運動量のナビエ・ストークス方程式、熱力学第一法則のエネルギー方程式として表されます。これらの方程式は、流体と流れ場を調べるために同時に考慮されます。

3つの保存方程式

質量保存

制御体積内の質量は、新しく生成されることも失われることもありません。

質量保存は、入口と出口の間のシステム全体の質量流量の差がゼロであることを示します。

$$ \frac{D\rho}{Dt}+\rho\left(\nabla\cdot\vec{V}\right)=0 \tag3$$

ここで、$\rho$ は密度、$V$ は速度、$\nabla$ は勾配演算子です。

$$ \vec{\nabla}=\vec{i}\frac{\partial}{\partial x}+\vec{j}\frac{\partial}{\partial y}+\vec{k}\frac{\partial}{\partial z} \tag4$$

密度が一定である間、流体は非圧縮性であると仮定します。このとき、連続性は以下のように単純化され、定常状態では次式で整理されます。

$$ \frac{D\rho}{Dt}=0 \longrightarrow \nabla\cdot\vec{V}=\frac{\partial u}{\partial x}+\frac{\partial v}{\partial y}+\frac{\partial w}{\partial z} =0 \tag5$$

運動量保存

運動量は運動中の質量を表し、物体の質量と速度の積として測定されます。

制御体積内の運動量は一定であるため、運動量保存則は運動量が生成も喪失もないことを意味します。運動量は、ニュートンの法則に基づく力の作用によってのみ変化します。

この説明は、ニュートンの運動第二法則の表現に従って設定されています:

$$ F=m \times a \tag6$$

ここで、$F$ は任意の粒子にかかる正味の力、$a$ は加速度、$m$ は質量です。流体の場合、この式を粒子の体積で表すと次のようになります。

$$ \rho\frac{DV}{Dt}=f=f_{body}+f_{surface} \tag7$$

ここで、$f$ は単位体積あたりの流体粒子にかかる力、$f_{body}$ は以下のように流体粒子の全質量にかかる力です。

$$ f_{body}=\rho g \tag8$$

$g$ は重力加速度です。流体粒子の表面を通して展開される外力$f_{surface}$ は、圧力と粘性力として次のように表されます。

$$ f_{surface}=\nabla\cdot\tau_{ij}=\frac{\partial\tau_{ij}}{\partial x_i}=f_{pressure}+f_{viscous} \tag9$$

$\tau_{ij}$ は応力テンソルです。ストークスによって与えられたニュートンの粘性流体の一般的な変形法則を適用すると、$\tau_{ij}$ は$^2$ のように表されます。

$$ \tau_{ij}=-p\delta_{ij}+\mu\left(\frac{\partial u_i}{\partial x_j}+\frac{\partial u_j}{\partial x_i}\right)+\delta_{ij}\lambda\nabla\cdot V \tag{10}$$

したがって、ニュートンの運動方程式は次のような形で指定することができます:

$$ \rho\frac{DV}{Dt}=\rho g+\nabla\cdot\tau_{ij} \tag{11}$$

(10)式を(11)式に代入すると、ニュートン粘性流体のNavier-Stokes方程式が1つの方程式になります:

$$ \rho\frac{DV}{Dt} = \rho g – \nabla p+\frac{\partial}{\partial x _ i}\left[\mu\left(\frac{\partial v _ i}{\partial x _ j} + \frac{\partial v _ j}{\partial x _ i}\right)+\delta _ {ij} \lambda\nabla\cdot V\right] \tag{12} $$

ここで、静圧は$p$ 、重力は$\rho\vec{g}$ です。式(12)は、過渡的な流れ場に対して便利です。$D/Dt$ は全微分で、次のような形を取ります。

$$ \frac{D(\,)}{Dt}=\frac{\partial(\,)}{\partial t}+u\frac{\partial(\,)}{\partial x}+v\frac{\partial(\,)}{\partial y}+w\frac{\partial(\,)}{\partial z}=\frac{\partial(\,)}{\partial t}+V\cdot\nabla(\,) \tag{13}$$

流体の密度が一定の場合、この方程式は大幅に簡略化され、粘性係数$\mu$ は一定と仮定され、式(12)のうち$\nabla\cdot V=0$が成り立ちます。したがって、非圧縮性の3次元流れに対するNavier-Stokes方程式は次のように表すことができます．

$$ \rho\frac{DV}{Dt}=\rho g-\nabla p + \mu\nabla^2V \tag{14}$$

速度が$V(u,v,w)$ であるとき、各成分について式を分解すると、以下のようになります。

$$ \rho\left(\frac{\partial u}{\partial t}+u\frac{\partial u}{\partial x}+v\frac{\partial u}{\partial y}+w\frac{\partial u}{\partial z}\right)=\rho g_x-\frac{\partial p}{\partial x}+\mu\left(\frac{\partial^2u}{\partial x^2}+\frac{\partial^2u}{\partial y^2}+\frac{\partial^2u}{\partial z^2}\right) \tag{15}$$

$$ \rho\left(\frac{\partial v}{\partial t}+u\frac{\partial v}{\partial x}+v\frac{\partial v}{\partial y}+w\frac{\partial v}{\partial z}\right)=\rho g_y-\frac{\partial p}{\partial y}+\mu\left(\frac{\partial^2v}{\partial x^2}+\frac{\partial^2v}{\partial y^2}+\frac{\partial^2v}{\partial z^2}\right) \tag{16}$$

$$ \rho\left(\frac{\partial w}{\partial t}+u\frac{\partial w}{\partial x}+v\frac{\partial w}{\partial y}+w\frac{\partial w}{\partial z}\right)=\rho g_z-\frac{\partial p}{\partial z}+\mu\left(\frac{\partial^2w}{\partial x^2}+\frac{\partial^2w}{\partial y^2}+\frac{\partial^2w}{\partial z^2}\right) \tag{17}$$

$p$ $u$は連続方程式と境界条件を適用して解を求める未知数です。また、熱を計算する必要がある場合には、エネルギー方程式を考慮する必要があります。

エネルギー保存

エネルギー保存は熱力学の第一法則であり、系に加えられる仕事と熱の合計は系の総エネルギーを増加させるというものです。

$$ dE_t=dQ+dW \tag{18}$$

ここで、$dQ$ は系に加えられた熱、$dW$ は系に加えられた仕事、$dE_t$ は系の総エネルギーの増加です。一般的なエネルギー方程式は下記の通りです。

$$ \rho\left[\frac{\partial h}{\partial t} + \nabla\cdot(hV)\right]=-\frac{\partial p}{\partial t}+\nabla\cdot(k\nabla T)+ \phi \tag{19}$$

ここで、$h$はエンタルピー、$k$ は熱伝導率です。

数学的な解析解 vs 数値計算

ナビエ・ストークス方程式は様々な複雑性を持つ非線形構造をしているため、厳密な解を求めることは困難です。そのため、方程式を解けるようにするには、様々な仮定が必要となります。

数学的モデルは、プロセス全体の一部であるパラメータ間の関係を与えるだけです。したがって、ナビエ・ストークス方程式の解法は、解析的方法と数値的方法のどちらでも実現可能です。

解析的手法は、ナビエ・ストークス方程式の非線形で複雑な構造をいくつかの仮定の範囲内で計算するだけです。これは、クエット流れ、ポアズイユ流れなど、単純で基本的な場合にのみ有効です。$^3$ 。

一方、流体力学のほとんどすべてのケースは、数学モデル中に非線形で複雑な構造を含んでおり、これらを無視することはできません。そのため，ナビエ・ストークス方程式の解法は、常微分方程式(ODE)や偏微分方程式(PDE)が遍在するいくつかの数値的手法の中で行われます。

流体流れのステップバイステップの計算解析は、図4に示すように記述することができます。

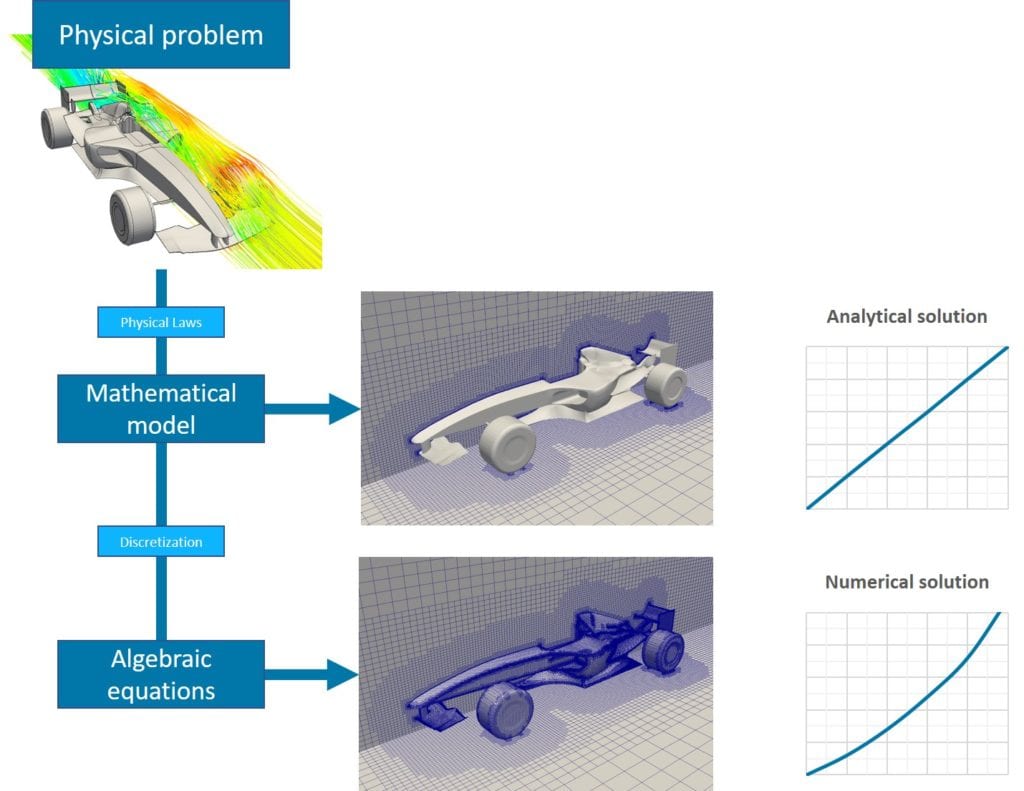
図4: 正確な領域と数値離散化は、PDEを線形化し、敏感な変数勾配を捉えるのに役立ちます。

SimScaleでは、上記のメッシュ分割による空間の離散化からシミュレーションの実施、結果の確認までをウェブブラウザで実施いただけます。

すぐにウェブブラウザで流体解析にトライ

時間領域

流体解析は、定常状態(時間に依存しない状態)または非定常状態(時間に依存する状態)で行うことができます。流れが定常の場合、流体やパラメータの運動が時間の変化に依存しないことを意味し、$\frac{\partial()}{\partial t}=0$ 、連続方程式と運動量方程式は次のようになります。

連続方程式:

$$ \frac{\partial(\rho u)}{\partial x}+\frac{\partial(\rho v)}{\partial y}+\frac{\partial(\rho w)}{\partial z}=0 \tag{20}$$

$x$ 方向のナビエ・ストークス方程式:

$$ \rho\left(u\frac{\partial u}{\partial x}+v\frac{\partial u}{\partial y}+w\frac{\partial u}{\partial z}\right) = \rho g_x-\frac{\partial p}{\partial x}+\mu\left(\frac{\partial^2u}{\partial x^2}+\frac{\partial^2u}{\partial y^2}+\frac{\partial^2u}{\partial z^2}\right) \tag{21}$$

定常流を仮定することで、いくつかの非線形項の影響が無視できるため、比較的低コストで解が得られます。一方、圧縮性、すなわち密度の変動は、方程式を複雑な形となり、数値解析のハードルとなっています。

圧縮性

あらゆる流体の流れは、様々な分子構造の範囲において圧縮性であるにもかかわらず、そのほとんどは非圧縮性であり、密度の変化は無視できます。

したがって、以下のように、流れが定常であるか否かにかかわらず、$\frac{\partial\rho}{\partial t}=0$ という項は切り捨てられます:

連続の式：

$$ \frac{\partial u}{\partial x}+\frac{\partial v}{\partial y}+\frac{\partial w}{\partial z}=0 \tag{22}$$

$x$ 方向のナビエ・ストークス方程式:

非圧縮性の仮定が合理的な方程式を提供するので、定常流の仮定を同時に適用することで、非線形項を無視することができます。$\frac{\partial()}{\partial t}=0$ 。

とはいえ、流速が臨界点を超えるような高速流は非圧縮性の仮定はできません。これはマッハ数($Ma$)によって決まります。マッハ数は、流速を周囲の媒体の音速と比較する無次元数です。次のように計算されます。$^3$ :

$$ Ma=\frac{V}{a}\ \tag{24}$$

ここで、$Ma$ はマッハ数、$V$ は流速、$a$ は流体中の音速で、その温度の関数です。

マッハ数が0.3未満の場合、流れは非圧縮性と考えられます。

マッハ数が0.3より大きい場合、つまり高速流の場合、密度の変化は無視できず、流れは圧縮性と見なされます。

例えば、自動車の速度が100$\frac{m}{s}$ より大きい場合、信頼性の高い数値解析を行うのに適したアプローチは圧縮性流れです。速度とは別に、地球物理学的流れでは密度変化に対する熱特性の影響を考慮する必要があります$^3$ 。

ナビエ・ストークス方程式に対するレイノルズ数の影響

レイノルズ数(Re)は慣性効果と粘性効果の比であり、ナビエ・ストークス方程式に影響を与えます。レイノルズ数が無限大 ($Re\longrightarrow\infty$) に近づくにつれて、粘性効果は無視できると推定され、ナビエ・ストークス方程式の粘性項は捨てられます。

したがって、オイラー方程式として記述されるナビエ・ストークス方程式の簡略形は、以下のように指定することができます$^8$ :

$x$ 方向:

$$ \rho\left(\frac{\partial u}{\partial t}+u\frac{\partial u}{\partial x}+v\frac{\partial u}{\partial y}+w\frac{\partial u}{\partial z}\right)=\rho g_x-\frac{\partial p}{\partial x} \tag{25}$$

粘性が流体にとって比較的重要であるにもかかわらず、非粘性流体モデルは、いくつかの特定のケースについて実際のプロセスを予測するための信頼性の高い数学モデルを部分的に提供します。例えば、物体上の高速な外部流れは、粘性流体アプローチが合理的に適合でき、広く使用されている近似です。一方、$Re\ll1$ では慣性効果は無視できると仮定され、ナビエ・ストークス方程式の関連項は削除されます。ナビエ・ストークス方程式の簡略形はクリープ流、またはストークス流れと呼ばれます$^8$ :

$x$ 方向のナビエ・ストークス方程式:

$$ \rho g_x-\frac{\partial p}{\partial x}+\mu\left(\frac{\partial^2u}{\partial x^2}+\frac{\partial^2u}{\partial y^2}+\frac{\partial^2u}{\partial z^2}\right)=0 \tag{26}$$

クリープ流は、粘性の影響がほとんどないため、溶岩の流れ、微生物の遊泳、ポリマーの流れ、潤滑などを調べるのに適しています。

ナビエ・ストークス方程式を用いた乱流モデリング

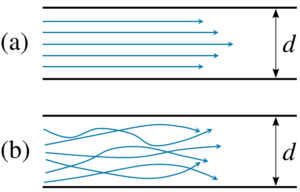
動的条件下での流体の挙動は、層流と乱流に分類することができます。層流は、流体の動きを正確に予測できる整然とした流れです。乱流はカオス的な挙動を示すため、予測が困難です。

レイノルズ数は、層流であれ乱流であれ、流速、長さ、粘性、流れの種類などいくつかの特性に関する流体の挙動を予測します。

流れが乱流である場合、数値解法を実行するために適切な数学モデルが必要となります。様々な乱流モデルが研究・提唱されており、それぞれカオス的な流体流れを検討するために異なる構造を持っています。

乱流をナビエ・ストークス方程式に適用することで、流体のカオス的な挙動をモデル化することができます。

乱流は層流の輸送量とは別に、瞬時値によって駆動されます。直接数値シミュレーション(DNS)は、ナビエ・ストークス方程式を瞬時値で解くアプローチです。DNSは、膨大な労力と高価な計算設備が必要です。

このようなハードルを回避するために、瞬時量を平均部分と揺らぎ部分の和で表すと次のようになります。

$$ u = \overline{u}+u’$$

$$ v = \overline{v}+v’$$

$$ w = \overline{w}+w’$$

$$ T= \overline{T}+T’$$

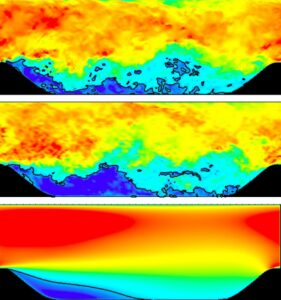
$u$ 、$v$ 、$w$ は速度成分、$T$ は温度です。定常および非定常条件での各値の差は図5のようになります。　

図5: 瞬間速度、平均速度、変動速度；a) 定常過程、b) 非定常過程$^8$

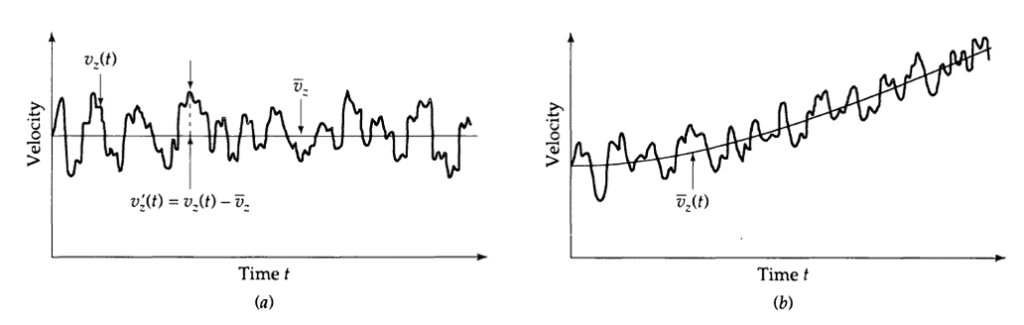
非線形性の原因となる瞬間的な値の代わりに、平均値を用いた数値解法を行うことで、「レイノルズ平均ナビエ・ストークス(RANS)方程式」$^4$ と呼ばれる乱流モデルが得られます。

ほとんどの工学的なケースでは、揺らぎは無視できます。したがって、RANS乱流モデルは、平均流方程式系を閉じるための手順です。レイノルズ平均ナビエ・ストークス(RANS)方程式の一般的な形式は以下のようになります:

連続方程式:

$$ \frac{\partial\overline{u}}{\partial x}+\frac{\partial\overline{v}}{\partial y}+\frac{\partial\overline{w}}{\partial z}=0 \tag{28}$$

$x$ 方向のナビエ・ストークス方程式:

$$ \rho\left(\frac{\partial\overline{u}}{\partial t}+\overline{u}\frac{\partial\overline{u}}{\partial x}+\overline{v}\frac{\partial\overline{u}}{\partial y}+\overline{w}\frac{\partial\overline{u}}{\partial z}\right)=\rho g_x-\frac{\partial\overline{p}}{\partial x}+\mu\left(\frac{\partial^2u}{\partial x^2}+\frac{\partial^2u}{\partial y^2}+\frac{\partial^2u}{\partial z^2}\right) \tag{29}$$

RANSの乱流モデルは、k-omega、k-epsilon、k-omega-SST、Spalart-Allmarasなどの手法によって異なります。同様に、Large Eddy Simulation(LES)も乱流の数学的手法の1つであり、いくつかのケースに適用されています。LESは、RANSよりも正確な結果を保証しますが、より多くの時間とコンピュータメモリを必要とします。LESは大きな渦は計算しますが、小さな渦をモデル化します$^4$ 。

ナビエ・ストークス方程式の単純な形式は、一相層流の動的条件下での速度、圧力、密度などの特性の変化のみを包含しています。ほとんどの工学用途では、数値シミュレーションのためにさらなる数学モデルが必要です。以下に、一般的な工学的問題とそれに関連する数学モデルを示します:

ダクト内の気流
単相流、層流/乱流、定常/非定常
開水路内の水流
多相流、層流/乱流、定常/非定常
シリンダー内の燃焼
多相流、層流・乱流、非定常、化学反応、伝熱、物質移動
水の凝縮・蒸発
混相流、層流・乱流、非定常、伝熱、物質移動

SimScaleでは、様々な乱流モデルを用いて、定常解析から非定常解析までクラウドのパワーを活用してシミュレーションを実施いただけます。

すぐにウェブブラウザで流体解析にトライ

マイクロ流体におけるナビエ・ストークス方程式

ナビエ・ストークス方程式は、マイクロ流体とも呼ばれる単一のバクテリアの運動のような、非常に小さなスケールの流れの物理モデルを補うことはできません。そのため、ナビエ・ストークス方程式を適切な数学モデルで補う必要があります。

クヌーセン数(Kn)は、分子構造の平均自由行程と観測スケールとの比を表す無次元数です。クヌーセン数による好ましいモデルを図6に示します。

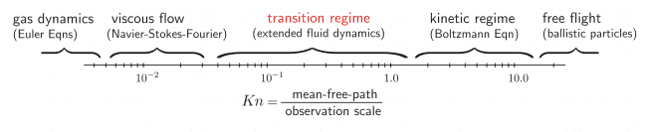
図6: クヌーセン数に従った流体の運動に関する好ましい数学モデル$^7$

参考

White, Frank (1991).Viscous Fluid Flow. 3rd Edition. McGraw-Hill Mechanical Engineering. ISBN-10: 0072402318.
Stokes, George (1851). “On the Effect of the Internal Friction of Fluids on the Motion of Pendulums”. Transactions of the Cambridge Philosophical Society. 9: 8–106.
White, Frank (2002). Fluid Mechanics. 4th edition. McGraw-Hill Higher Education. ISBN: 0-07-228192-8.
Cebeci, T., Shao, J.P., Kafyeke, F., Laurendeau, E (2005). Computational Fluid Dynamics for Engineers. Horizon Publishing Inc. ISBN: 0-9766545-0-4.
http://www.dgp.toronto.edu/people/stam/reality/Research/pdf/GDC03.pdf
https://software.intel.com/en-us/articles/fluid-simulation-for-video-games-part-1
http://www.mathcces.rwth-aachen.de/2research/0mms/0gases/start
Bird, R.B., Stewart, W.E. and Lightfoot, E.N. (2001). Transport Phenomena, 2th edition. John Wiley Sons. ISBN 0-471-41077-2.
https://en.wikipedia.org/wiki/Isaac_Newton
https://en.wikipedia.org/wiki/Claude-Louis_Navier
https://en.wikipedia.org/wiki/Sir_George_Stokes,_1st_Baronet