輸送方程式はスカラー量が流体内でどのように輸送されるかを記述するもので、パッシブスカラー、温度、運動量など多くのスカラーに適用されます。一般的な輸送方程式は以下の通りです:

$$ \frac{\partial \phi}{\partial t} = \mathbf{\nabla} \cdot \boldsymbol{u} \phi \hspace{2mm} – \mathbf{\nabla} \cdot \Gamma \mathbf{\nabla} \phi + S \tag{1}$$

ここで

\(\phi\) は任意のスカラー、

\(\frac{\partial \phi}{\partial t}\)はスカラーの経時変化、

\(\boldsymbol{u}\)は速度ベクトル(\(u, v, w\))、

\(\nabla\)はナブラと呼ばれスカラーの勾配を、

\(\mathbf{\nabla} \cdot\)はスカラーの発散を、

\(S\) はソース項を表します。

数学的な観点からは、輸送方程式は対流拡散方程式とも呼ばれ、一次の PDE(偏微分方程式)です。対流拡散方程式は最も一般的な輸送モデルの基礎となっています。

この方程式が難しそうに見えても、心配しないでください。

輸送方程式は保存方程式の一般化と見ることができます:

$$ \frac{\partial \phi}{\partial t} = \mathbf{\nabla} \cdot J + S \tag{2}$$

ここで\(J\) はスカラーの流束を示します。

輸送方程式の理解

まず、連続方程式\(^2\) からスカラー輸送方程式\(^1\) に至る主な構成要素を理解することから始めましょう。

基本問題とその定義

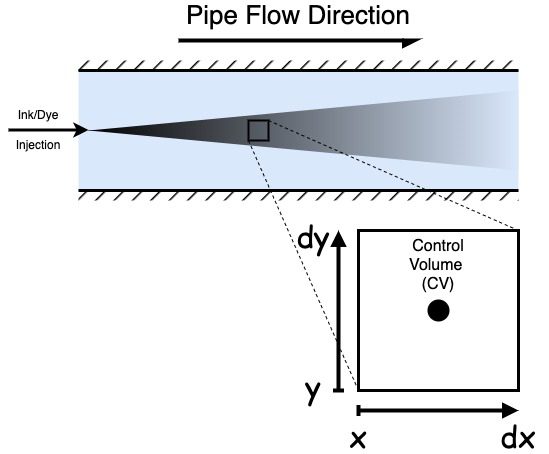
図1：スカラー(インクまたは染料)が流れ方向に沿って対流し、流れ方向を横切って拡散する単純な流体の問題

輸送方程式の背後にある数学について議論するとき、我々はいくつかの用語に精通していなければなりません。まず、制御体積とは小さな、任意形状の流体体積のことです。CFDの文脈でボリュームを考える場合、メッシュ生成時にできる多面体形状のボリュームになりがちです。同じような形状のボリュームは数多く存在します。

通常、体積は限りなく小さいか、その大きさがゼロに近づくと考えます。体積が小さければ小さいほど、解の精度は向上します。

連続方程式

連続の原理は、任意の微分制御体積におけるスカラー量の変化率は、制御体積内部での生成または消費とともに、系内外へのスカラー量の流れと拡散によって与えられることを述べています。

実際には、体積内のある量の濃度変化は、境界を横切る量の流れと、体積内部で生成または除去される量のバランスです。数学的な観点からは、このバランスを式で表すことができます\(^2\) :

$$ \frac{\partial \phi}{\partial t} = \mathbf{\nabla} \cdot J + S \tag{2}$$

スカラー流束

フラックス\(J\) とは、何かがどのように動いたり流れたりするかを表す言い方にすぎません。この場合、スカラーフラックスとはスカラーがどのように動き、どのように流れるかということです。流体では、スカラーが流体の流れとともにどのように動くか(対流)を考えますが、流れの方向とは関係なく、スカラーが流体中にどのように拡散するか(拡散)も考えます。

数学的には

$$ J = J_{convection} – J_{diffusion} \tag{3}$$

拡散がなぜ負の慣例を持つかについては後述しますが、多分もうお分かりでしょう。

この項は次のように書けます:

$$ J_{convection} = u \phi \tag{4}$$

$$ J_{diffusion} = \Gamma \mathbf{\nabla} \phi \tag{5}$$

ここで\(\Gamma\) は拡散係数です。この値が大きいほど、拡散は速くなります。

各用語のイメージ

対流:

拡散:

フラックス項は、対流と拡散によってスカラーが時間とともに空間的にどのように移動するかを表していることがわかります。

ソース項：

\(S\)ソース項は、制御体積の内部で生成または破壊されるスカラー量の量を表します。

輸送方程式をまとめる

式\(^4\) と式\(^5\) を式\(^3\) に、式\(^3\) を式\(^2\) に当てはめると、次のようになります:

$$ \frac{\partial \phi}{\partial t} = \mathbf{\nabla} \cdot(\boldsymbol{u} \phi – \Gamma \mathbf{\nabla} \phi) + S \tag{6}$$

式を展開すると、輸送方程式の一般化された形\(^1\) が得られます:

$$ \underbrace{\frac{\partial \phi}{\partial t}}_{\substack{\text{unsteady} \\ \text{term}}} = \underbrace{\mathbf{\nabla} \cdot \boldsymbol{u} \phi \vphantom{\frac{\partial \phi}{\partial t}}}_{\substack{\text{Convection} \\ \text{term}}} \hspace{2mm} – \underbrace{\mathbf{\nabla} \cdot \Gamma \mathbf{\nabla} \phi \vphantom{\frac{\partial \phi}{\partial t}}}_{\substack{\text{Diffusion} \\ \text{term}}} + \underbrace{S \vphantom{\frac{\partial \phi}{\partial t}}}_{\substack{\text{Source} \\ \text{term}}} \tag{1}$$

CFDにおける輸送方程式

輸送方程式はほとんどのCFDコードの基礎となっており、そこからナビエ・ストークス方程式、エネルギー方程式、その他多くの保存式が導かれます。

ここでは、輸送方程式からどのように派生するかを簡単に説明します。

エネルギー方程式

熱シミュレーションでは、温度場(スカラー)は対流拡散方程式に従って輸送されます。この場合、科学界では次のような表記が一般的です。

$$ (\rho c_{p})\frac{\partial T}{\partial t} = (\rho c_{p})\nabla\cdot (uT) \ -\nabla\cdot (k\nabla T) + \frac{Q_{\text{source}}}{V}$$

ここで

• \(\rho\) は物質密度
• \(c_p\) は比熱容量
• \(T\) は温度
• \(k\) は熱伝導率
• \(\frac{Q_{\text{source}}}{V}\) は体積熱流束

式中のすべての項の単位は\([mass^{1}][length^{-1}][time^{-3}]\) で、これは体積熱流束としても知られています。

熱源の項には、放射の項や、湿度などの複雑な相互作用による他の項を含めることもできます。

パッシブスカラー

私たちは、多くの汚染物質や汚染源をパッシブスカラーであると考えています。パッシブスカラーは流れ場に影響を与えないため、受動的です。パッシブスカラーの使用例としては、工業地帯の汚染物質が空気中をどのように移動し、住宅地の空気にどのような影響を与えるかを追跡することが挙げられます。この汚染物質は、好ましくない臭いのする空気という単純なものです。パッシブスカラーはパッシブ種と呼ばれることもあります。

$$ \underbrace{\frac{\partial \phi}{\partial t}}_{\substack{\text{unsteady} \\ \text{term}}} = \underbrace{\mathbf{\nabla} \cdot \boldsymbol{u} \phi \vphantom{\frac{\partial \phi}{\partial t}}}_{\substack{\text{Convection} \\ \text{term}}} \hspace{2mm} – \underbrace{\mathbf{\nabla} \cdot \Gamma \mathbf{\nabla} \phi \vphantom{\frac{\partial \phi}{\partial t}}}_{\substack{\text{Diffusion} \\ \text{term}}} + \underbrace{S \vphantom{\frac{\partial \phi}{\partial t}}}_{\substack{\text{Source} \\ \text{term}}} \tag{1}$$

\(^1\)

対流項は、汚染物質が速度場とともにどのように移動するかを記述します。拡散項は、汚染物質が周囲の空気にどれだけ拡散するかを記述します。発生源項は、ある体積に受動スカラーを注入するために使用します。この例では、水処理プラントなどが該当します。

図3: 汚染源を表す受動スカラーの例

SimScaleでは、拡散係数\(\Gamma\) はシミュレーションツリー内のモデルノードで定義されます。ソース項は、シミュレーションツリーのアドバンスコンセプトのパッシブスカラーソースに定義されます。パッシブスカラーソースは、体積パッシブスカラーソースまたは体積またはプリミティブに割り当てられたパッシブスカラーソースのいずれかです。

輸送方程式の導出

図1: 輸送方程式の導出方向と命名規則

まず、流体中のスカラーの動きを記述する簡単な方程式を考えてみましょう。これはオイラー参照フレームで行います。つまり、考える体積は静的で、流体はその体積の中を出入りします。

保存方程式から始めるのがよく、そこでは濃度に関するスカラーを保存します。質量保存則は次のように書きます:

$$ \dot{m} = \rho.A. \boldsymbol{u} \tag{11}$$

質量流量を体積の関数として表すと、次の式が得られます:

$$ \frac{d \rho V}{d t} = \rho A \boldsymbol{u}$$ より一般的には$$ \frac{d \phi V}{d t} = \phi A \boldsymbol{u}\tag{12}$$

\(\phi\) は任意のスカラー濃度で、単位は 。スカラー単位は問題に適したものであれば何でもかまいません。\([\text{scalar unit}^{1}][length^{-3}]\)

これを再整理して、非常に小さな体積について考えてみましょう:

$$ \frac{\partial \phi}{\partial t} = \frac{A \boldsymbol{u} \phi }{V} \tag{13}$$

\(\frac{\partial \phi}{\partial t}\) 単位\([\text{scalar unit}^{1}][length^{-3}][time^{-1}] \)

以下の導出では、各項の単位がこれらの単位と一致することを確認するために、各主要ステップでチェックを行います。

ここでは偏導関数、つまりスカラーの時間的変化について考えてみましょう。体積中のスカラーの量は対流、拡散、発生源などいくつかの要因によって変化します。

$$ \frac{\partial \phi}{\partial t} = \frac{\partial \phi}{\partial t} \Bigr|_{convection} + \frac{\partial \phi}{\partial t} \Bigr|_{diffusion} + \frac{\partial \phi}{\partial t} \Bigr|_{source}\tag{14}$$

上記のステップを書く理由は、ミスを少なくするためです。

対流

対流の項は二つのフラックスの中で最も簡単なものです。式に戻りましょう:

$$ \frac{\partial \phi V}{\partial t}\Bigr|_{convection} = \boldsymbol{u} \phi A \tag{15}$$

以下のステップではフラックスを表す記号\(J\) を導入します.フラックスは流体力学ではよく使われる用語で，任意の境界をどれだけのスカラーが流れるかを表します．単位は\([\text{scalar unit}^{1}][length^{-2}][time^{-1}]\) 。

対流フラックスは次のように書くことができます:

$$ J = \boldsymbol{u} \phi \tag{16}$$

フラックスを式\(^{15}\) に代入すると, 簡単にフラックスを分離することができます.これは対流の項ではあまり重要ではありませんが, 拡散の項では矛盾のないようにするために非常に役に立ちます.

$$ \frac{\partial \phi V}{\partial t}\Bigr|_{convection} = JA \tag{17}$$

これをさらに進めるために, 全フラックスをいくつかの要素に分割し, フラックス・インからフラックス・アウトを引いたものにします:

$$ \frac{\partial \rho \phi V}{\partial t}\Bigr|_{convection} = J_{in}A – J_{out}A \tag{18}$$

しかし、これらの成分をx成分とy成分に分けることもできます。

ここでは2次元の輸送方程式を導出していますが、1次元や3次元の問題にも同様に適用できます。最後にn次元に一般化します。2次元の導出として、体積は2次元、面積は1次元です。

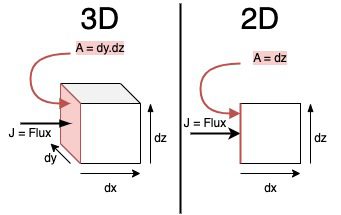
3次元と2次元の体積と表面積の違い

そこで、私たちの慣例では、2Dの場合、x境界の面積をdyとし、面積によるフラックス・インと面積によるフラックス・アウトを次のように書くことができます:

$$ J_{in}A = J\Bigr|_{x}.dy + J\Bigr|_{y}.dx\tag{19} $$

$$ J_{out}A = J\Bigr|_{x+dx}.dy + J\Bigr|_{y+dy}.dx\tag{20} $$

フラックスが境界ごとにあるように、面積も境界ごとにあるからです。

式\(^{16}\)をJに代入します:

$$ J_{in}A = \phi u\Bigr|_{x}.dy + \phi v\Bigr|_{y}.dx\tag{21} $$

$$ J_{out}A = \phi u\Bigr|_{x+dx}.dy + \phi v\Bigr|_{y+dy}.dx\tag{22} $$

速度成分が方向によってどのように変化するかに注目してください。速度ベクトルは太字の記号で表すことができます:

$$ \boldsymbol{u} = (u, v, w) $$

式\(^{21,22}\) を式\(^{18}\) に代入すると、次のようになります:

$$ \frac{\partial \phi V}{\partial t}\Bigr|_{convection} = \phi u \Bigr|_{x}.dy – \phi u \Bigr|_{x+dx}.dy + \phi v \Bigr|_{y}.dx – \phi v\Bigr|_{y+dy}.dx \tag{23}$$

また、二次元の体積\(V = dx.dy\) もわかります。式\(^{23}\) を\(dx.dy\) で割ると、次のようになります:

$$ \frac{\partial \phi}{\partial t}\Bigr|_{convection} = \frac{\phi u\Bigr|_{x}.dy – \phi u\Bigr|_{x+dx}.dy}{dx.dy} + \frac{ \phi v \Bigr|_{y}.dx – \phi v \Bigr|_{y+dy}.dx}{dx.dy} \tag{24}$$

となります:

$$ \frac{\partial \phi}{\partial t}\Bigr|_{convection} = \frac{\rho u \Bigr|_{x} – \phi u \Bigr|_{x+dx}}{dx} + \frac{\phi v \Bigr|_{y} – \phi v \Bigr|_{y+dy}}{dy} \tag{25}$$

これは偏導関数なので、次のように書き換えることができます:

$$ \frac{\partial \phi}{\partial t}\Bigr|_{convection} = \frac{\partial \phi u}{\partial x} + \frac{\partial \phi v}{\partial y} \tag{26}$$

\(\nabla\) \(\nabla\) は勾配と呼ばれることもあります．しかし、厳密にはそうではありません。スカラーについては

$$ \nabla \phi = (\frac{\partial \phi}{\partial x}, \frac{\partial \phi}{\partial y}, \frac{\partial \phi}{\partial z}) \tag{27}$$

しかし、ベクトルの場合は、\(\boldsymbol{u}\) のように書きます:

$$ \nabla \boldsymbol{u} = (\frac{\partial u}{\partial x}, \frac{\partial v}{\partial y}, \frac{\partial w}{\partial z}) \tag{28}$$

もう一つ考慮しなければならないのは、\(\nabla \cdot\) またはダイバージェンスと呼ばれるものです:

$$ \nabla \cdot \boldsymbol{u} = \frac{\partial u}{\partial x} + \frac{\partial v}{\partial y} + \frac{\partial w}{\partial z} \tag{29}$$

これは最後の単純化のステップに入ります。式\(^{25}\) の\(\nabla \cdot\) とほとんど同じものがあることに注目してください。式\(^{29}\) を\(\nabla \cdot \phi \boldsymbol{u}\) に代入してみましょう:

$$ \boxed{\frac{\partial \phi}{\partial t}\Bigr|_{convection} = \nabla \cdot \boldsymbol{u} \phi }\tag{30}$$

ここで対流項の導出が予想される単位に合っているかどうかを確認する必要があります.先ほど、スカラー濃度の変化は\([\text{scalar unit}^{1}][length^{-3}][time^{-1}]\) の単位であると述べましたが、もしスカラーの単位が kg で、メートル単位であれば、\(\frac{kg}{m^{3}s}\) のようになります。

ここで、\(\nabla \cdot \boldsymbol{u} \phi\) を1次元で表すと、\(\frac{\partial \boldsymbol{u} \phi}{\partial x}\) となります。スカラー単位がkgで、メートル単位系を使っていると仮定して、単位を書き出します:

\(\phi = \frac{kg}{m^{3}}\)

\(u = \frac{m}{s}\)

\(\frac{\partial}{\partial x} = \frac{1}{m}\)

これを単純化して単位系に一般化し、スカラー単位を使うと、\([\text{scalar unit}^{1}][length^{-3}][time^{-1}]\) と書くことができます。これは予想と一致し、ここまでに間違いがなかったことを証明します。これは良い練習で、長い目で見れば最終的に時間の節約になります。

拡散

対流項では、スカラー\(\phi\) が流れ場\(\boldsymbol{u}\) と共に輸送され、スカラー保存方程式に基づくフラックス\(J= \boldsymbol{u} \phi \) の基礎となることがわかっていました。同様に, 拡散項についても\(J\) を定義する必要があります.拡散では、スカラー濃度の差が重要な役割を果たします:

$$ J \propto \frac{d \phi}{ d x} \tag{31}$$

さて、定数を入れて方程式を作ると、フリックの第一法則によく似ていることに気づくかもしれませんので、定数を入れる代わりに拡散係数を入れてみましょう。また、拡散係数は正の数ですが、スカラーは高濃度から低濃度へ移動するので(負の勾配)、負の定数も導入しなければなりません。

$$ J = – \Gamma \frac{d \phi}{ d x} \tag{32}$$

これを多方向から見ようと思えば、2次元の場合はこう言えます:

$$ \boldsymbol{J} = (- \Gamma \frac{d \phi}{ d x}, – \Gamma \frac{d \phi}{ d y}) = -\Gamma \nabla \phi \tag{33}$$

先ほどと同じように、\(^{18}\) 式を使いますが、今回は拡散について考えます:

$$ \frac{\partial \phi V}{\partial t}\Bigr|_{diffusion} = J_{in}A – J_{out}A \tag{34} $$

対流の場合と同じように, 流入と流出の拡散を定義します:

$$ J_{in}A = J\Bigr|_{x}.dy + J\Bigr|_{y}.dx\tag{35} $$

$$ J_{out}A = J\Bigr|_{x+dx}.dy + \Bigr|_{y+dy}.dx\tag{36} $$

しかし, この段階でジレンマが生じます.もし J を代入してしまうと,\(^{32}\) 式の導関数を簡略化することが困難になってしまう.幸いなことに、テイラー級数展開による助けがあります。次へのテイラー級数展開は以下の通りです:

\(f(x) = f(a) + f'(a).(x-a)\) または、特に我々の問題に対して \(f(x+dx) = f(x) – f'(x).dx\)

そして、これを方程式\(^{36}\) に代入することができます:

$$ J_{out}A = J\Bigr|_{x}\partial y – \frac{\partial J}{\partial x}.\Bigr|_{x} \partial x \partial y + J\Bigr|_{y} \partial x- \frac{\partial J}{\partial y}.\Bigr|_{y} \partial y \partial x\tag{37}$$

式\(^{35,37}\) を式\(^{34}\) に代入すると次のようになります:

$$ \frac{\partial \phi V}{\partial t}\Bigr|_{diffusion} = J\Bigr|_{x} \partial y – J\Bigr|_{x} \partial y+ \frac{\partial J}{\partial x}.\Bigr|_{x} \partial x \partial y + J\Bigr|_{y} \partial x – J\Bigr|_{y} \partial x + \frac{\partial J}{\partial y}.\Bigr|_{y} \partial y \partial x\tag{38} $$

となります:

$$ \frac{\partial \phi V}{\partial t}\Bigr|_{diffusion} = \partial J\Bigr|_{x} \partial y + \partial J\Bigr|_{y} \partial x \tag{39} $$

そして先ほどと同様に、体積\(V=\partial x \partial y\) 、式\(^39\) を\(V\) で割ると次のようになります:

$$ \frac{\partial \phi}{\partial t}\Bigr|_{diffusion} = \frac{\partial J\Bigr|_{x}}{\partial x} + \frac{\partial J\Bigr|_{y}}{\partial y}\tag{40} $$

さて、\(\nabla \cdot \boldsymbol{J}\) は式\(^{29}\) で定義されているので、これを次のように書き換えることができます:

$$ \frac{\partial \phi}{\partial t}\Bigr|_{diffusion} = \nabla \cdot \boldsymbol{J} \tag{41}$$

と書き換え、式\(^{33}\) を式\(^{41}\) に代入すると、最終的な拡散項が得られます:

$$ \boxed{\frac{\partial \phi}{\partial t}\Bigr|_{diffusion} = \ – \nabla \cdot \Gamma \nabla \phi }\tag{42}$$

ここでも単位を再確認する必要があります。1次元の拡散項はFlickの第二法則\( – \Gamma \frac{\partial^{2} \phi}{\partial x^{2}}\) 。

\(\Gamma\) の単位は の単位は の単位は\([length^{2}][time^{-1}]\)

\(\frac{\partial^{2}}{\partial x^{2}}\) \([length^{-2}]\)

\(\phi\) \([\text{scalar unit}^{1}][length^{-3}]\)

すべての単位を足すと\([\text{scalar unit}^{1 mm}][length^{-3}][time^{-1}]\) となります。

ソース項

対流項や拡散項とは対照的に、ソース項は単純です。これは輸送方程式に直接加えるものであり、体積に経時的な濃度を加えるので、次のように表されます:

$$ \boxed{\frac{\partial \phi}{\partial t}\Bigr|_{source} = S} \tag{43}$$

輸送方程式の項

輸送方程式を3つの項に分割し、最後に代入する方が簡単だった理由がわかりました。最後のステップでは、方程式\(^{\text{30, 42, 43}}\) を方程式\(^{14}\) に代入して、方程式\(^{1}\) を得ます:

$$ \underbrace{\frac{\partial \phi}{\partial t}}_{\substack{\text{unsteady} \\ \text{term}}} = \underbrace{\mathbf{\nabla} \cdot \boldsymbol{u} \phi \vphantom{\frac{\partial \phi}{\partial t}}}_{\substack{\text{Convection} \\ \text{term}}} \hspace{2mm} – \underbrace{\mathbf{\nabla} \cdot \Gamma \mathbf{\nabla} \phi \vphantom{\frac{\partial \phi}{\partial t}}}_{\substack{\text{Diffusion} \\ \text{term}}} + \underbrace{S \vphantom{\frac{\partial \phi}{\partial t}}}_{\substack{\text{Source} \\ \text{term}}} \tag{1}$$