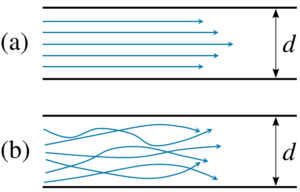
流体力学において乱流とは、渦や旋回、流れの不安定性が発生する不規則な流れを指します。乱流は、運動量の大きい対流と運動量の小さい拡散によって支配されます。層流とは、流体が層間に乱れのない平行な層で流れることです。

乱流領域は、自然現象や工学的応用において非常に頻繁に見られます。例えば、タバコの煙の上昇、滝、動脈の血流、地上の大気循環の大部分などが挙げられます。

工学的な応用例としては、自動車、飛行機、船舶などのあらゆる乗り物の空気力学や、熱交換器、焼き入れプロセス、鋼鉄の連続鋳造などの多くの工業的な応用例で乱流領域が発生します。

乱流の構造

1920年、ルイス・フライ・リチャードソン(Lewis Fry Richardson)は、『Weather Prediction by Numerical Process(数値過程による気象予測)』$^1$ に掲載された有名な韻文を通じて、気象学的応用のための乱流の構造に関する研究をまとめました:

「大きな渦には小さな渦があり、小さな渦にはさらに小さな渦があり、そして粘性へと続く」$^1$

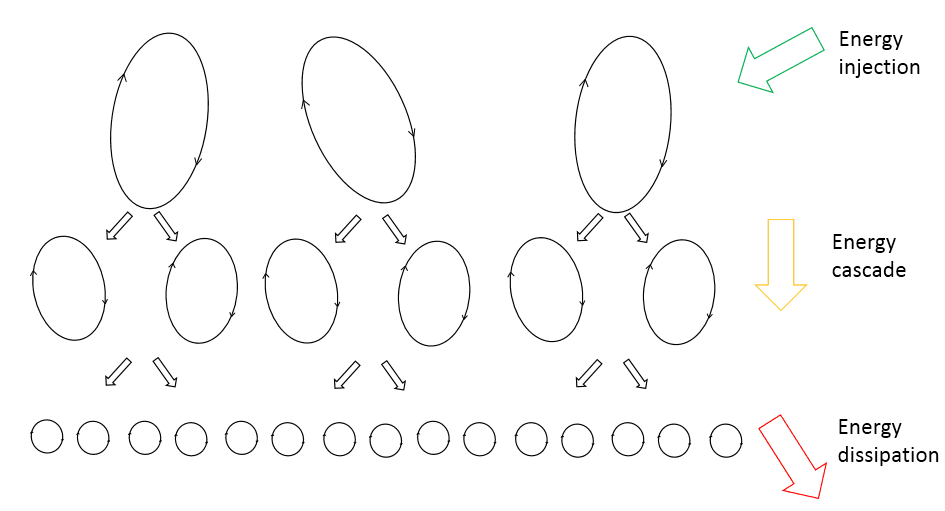
大きな渦は非常に慣性的で不安定になりがちです。大きな渦は慣性力が強く、不安定になりがちです。渦の運動は、運動エネルギーの局所的な移動によって、小さな渦に栄養を与えます。これらの小さな渦も同じプロセスを経て、親渦のエネルギーを受け継ぐさらに小さな渦を生み出します。

このようなエネルギーの移動は通常「エネルギーカスケード」と呼ばれ、主に慣性的であるため、流体の粘性が運動エネルギーを効果的に散逸させることができるような十分に小さな長さスケールに達するまで、エネルギーの散逸はほとんど起こりません。このプロセスは図1に描かれています。

リチャードソンの研究は、乱流がエネルギーを必要とするという本質的な特徴を強調しています。乱流は、外部からのエネルギー源が供給されない限り、エネルギーを散逸し、最小のスケールで層流へと減衰します。

図1: リチャードソンのエネルギーカスケードは、エネルギー散逸が起こるまで、親渦が次々と小さな渦に分解していく様子を示しています。

最小乱流スケール

乱流の複雑さとその偶発的な挙動から、科学者は乱流の流れを記述するために統計モデルを使用するようになりました。

1941年、KolmogorovはRichardsonの理論$^2$ を改良しました。Kolmogorovは、レイノルズ数が十分に高い場合、小規模な渦は等方的であるが、大規模な渦は異方的である可能性があると仮定しました(または、いずれにせよ、特定の領域のトポロジーに依存します)。

この仮定は、小さな渦の統計解析が特定の形状に依存せず、すべての乱流に対して普遍的であることを意味するため、非常に重要です。この仮説の下で、Kolmogorovは最小の乱流スケール(「Kolmogorovマイクロスケール」として知られる)の主な特徴を統計的に次のように記述しました:

コルモゴロフの長さスケール	$\eta = \left(\frac{\nu^3}{\epsilon}\right)^{0.25}$
コルモゴロフ時間スケール	$\tau=\left(\frac{\nu}{\epsilon}\right)^{0.5}$
コルモゴロフ速度スケール	$u=\left(\nu\epsilon\right)^{0.25}$

表1: コルモゴロフのミクロスケール

ここで

$\nu$ は動粘性係数
$\epsilon$ は乱流の運動エネルギー
$\eta$、$\tau$および$u$は、それぞれ最小の渦の特徴的な長さ、周期(または「回転時間」)、速度を示します。

レイノルズ数

乱流に関する科学的研究の本格的な始まりは、19$^{th}$ 世紀後半のオズボーン・レイノルズの研究にあります。レイノルズは実験的調査を通じて、層流と乱流の間の遷移を示しました。レイノルズはまた、この遷移が慣性力と粘性力の比に直接関係することを示唆しました。この比は、1851年にジョージ・ガブリエル・ストークスによって計算され、これを広めたオズボーン・レイノルズにちなんで「レイノルズ数」と名付けられました。

この無次元数は次のように定義されます:

$$ Re = \frac{\rho ud}{\mu}=\frac{ud}{\nu} \tag{1}$$

ここで

$\rho$ は流体の密度
$u$ は巨視的な流速
$d$ は特性長(または水力直径)
$\mu$ は流体の動的粘度
$\nu$ は流体の動粘度。

乱流は、$Re$ が「臨界レイノルズ数」と呼ばれるある閾値(適用先の体系と境界条件に依存)を超えたときに発生します。

CFDにおける乱流モデリング

流体の運動を規定する主な方程式は、保存則の適用によって構成され、これらの方程式はナビエ・ストークス方程式と呼ばれます。流体の運動は、流れが層流であるか乱流であるかにかかわらず、ナビエ・ストークス方程式によって完全に記述されます。以下では、流体運動をモデル化できる非圧縮形式を提供します:

$$ \rho\partial_tu_i+\rho u_ju_{i,j}=-\rho p_{,i}+\mu u_{i,jj} \tag{2}$$

$$ u_{i,i}=0 \tag{3}$$

ここで

$u$ は流速
$p$ は流体の圧力
$\rho$ は流体の密度
$\mu$ は流体の動粘度

ナビエ・ストークス方程式は、主に対流加速度項$u_ju_{i,j}$ に起因する非線形性のため、本質的に解くのが非常に困難です。そのため、流体領域を離散化することによって、適切な初期条件と境界条件による数値解法を可能にするさまざまな方法論が開発されました。

SimScaleでは、ウェブブラウザでシミュレーションの実施、結果の確認までを実施いただけます。

ウェブブラウザですぐに流体解析にトライ

乱流モデリング手法の概要

CFD における乱流のモデリングには様々なアプローチがありますが、その主な特徴は問題のメッシュ解像度にあり、シミュレーションに必要な計算能力を定義します。

直接数値シミュレーション(Direct Numerical Simulation: DNS)

乱流の最小の空間スケールと時間スケールを解像できる非常に高解像度のメッシュは、直接数値シミュレーション(DNS)と呼ばれます。DNSでは乱流の構造が完全に表現されます。しかし、DNSの計算コストは非常に高い。そのため、DNSはレイノルズ数が小さい小規模な問題に限定されます$^3$ 。

ラージ・エディ・シミュレーション(Large Eddy Simulation: LES)

ラージ・エディ・シミュレーション(LES)乱流モデルでは、乱流の最小スケールを空間的にフィルタリングしてモデル化します。一方、最も大きく、最もエネルギーを含むスケールはメッシュによって直接分解されます。このアプローチでは、DNSよりもメッシュ解像度を粗くすることができるため、この手法をより普遍的でさまざまな流体流れ問題に適用することができます。

離散渦シミュレーション(Detached Eddy Simulation: DES)

Detached Eddy Simulation乱流モデルは、RANSモデルとLESモデルの両方の手法を組み合わせたものです。乱流の長さスケールが最大グリッドサイズよりも小さい壁近傍の領域では、DESモデルはその領域にRANSモデルを割り当てます。その結果、乱流の長さスケールが最大グリッドサイズよりも大きい領域では、DESモデルがその領域にLESモデルを割り当てます。このアプローチでは、純粋なLESシミュレーションほどグリッド解像度を上げる必要がないため、シミュレーションにかかる計算コストを削減することができます。

レイノルズ平均ナビエ・ストークス(Reynolds Averaged Navier Stokes: RANS)

レイノルズ平均ナビエ・ストークス(RANS)は、計算負荷の少ない手法です。これは、流れ場の時間平均解法を使用します。レイノルズ平均プロセスは、レイノルズ応力として知られる追加項をナビエ・ストークス方程式に導入します。

非圧縮性ニュートン流体のNSEをもう一度考えてみましょう:

$$ \rho\partial_tu_i+\rho u_ju_{i,j}=-\rho p_{,i}+\mu u_{i,jj} \tag{2}$$

$$ u_{i,i}=0 \tag{3}$$

その原理は、流れを平均流と乱流／非定常流の和として考えることです。定常平均流速は全体流速のファーブル平均として計算できます:

$$ U_i=\lim_{T\rightarrow\infty}\frac{1}{T}\int_0^Tu\: dt \tag{4}$$

したがって、速度は次のように分解できます:

$$ u_i=U_i+u’_i \tag{5}$$

ここで、$U$ は平均速度、$u’$ は乱流速度(または乱流スケール)です。$T$ は平均化時間スケールで、問題の良い近似を得るためには十分に小さくなければなりませんが、乱流の時間スケール、すなわちコルモゴロフの回転時間よりも十分に大きくなければなりません。平均化された量をナビエ・ストークス方程式に代入すると、RANS方程式が得られます:

$$ \rho U_j U_{i,j} =-\rho P_{i} +\mu U_{i,jj} -\left( u_{i}’ u_{j}’\right) _j \tag{6}$$

$$ U_{i,i}=0 \tag{7}$$

ここで、$\left( u_{i}’ u_{j}’\right) _j$ は通常「レイノルズ応力」と呼ばれ、平均的な流れに対する小規模な乱流の影響を表します。RANS方程式は、未知数の数が方程式の数より多いため、一意解を持ちません。そのため、問題を解決するために追加の方程式が必要となります。CFDで使用される最も一般的な方法は、レイノルズ応力とせん断速度をブジネスクの関係で関連付けることです:

$$ u_i’u_j’=2\frac{\mu_t}{\rho}S_{ij} \qquad with\qquad S_{ij}=\frac{1}{2}\left(U_{i,j}+U_{j,i}\right) \tag{8}$$

ここで、$\mu_t$ は乱流粘性率で、通常は乱流モデル$^4$ から計算されます。

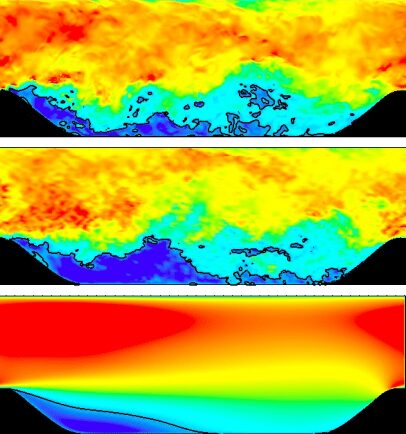
様々な乱流モデリングアプローチの基本的な概念を理解したところで、図2に示すように、定性的な視覚的説明でそれを補完することができます。これは、DNS、LES、RANSを比較したときに、乱流スケールがどの程度まで観察できるかを示しています。

図2: 乱流のシミュレーション(^5) 下: RANS、中: LES、上: DNS

乱流のアプリケーション

乱流は、多くの自然現象(河川の流れ、大気の流れ、自然対流など)や工学的アプリケーション(都市における風の流れ、空気力学解析、連続鋳造、急冷プロセス、冷却/加熱システムなど)に存在します。

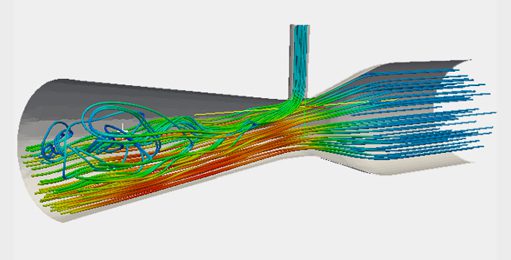
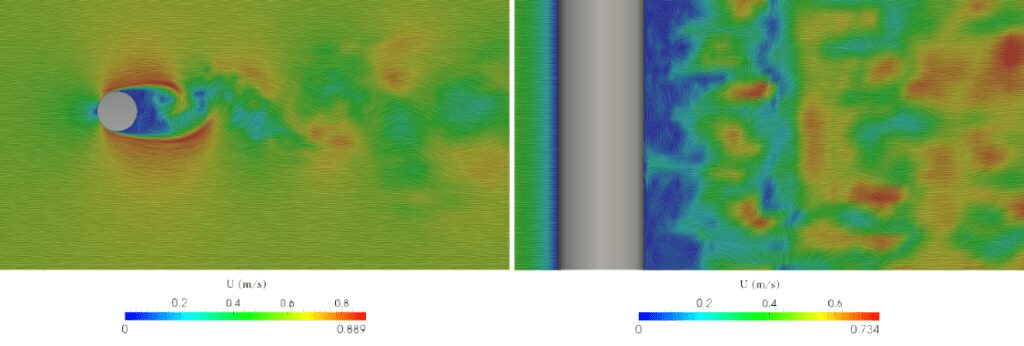
このセクションでは、SimScaleを使用した2つの小規模なアプリケーションについて報告します。1つ目(図3)は、円柱周りの流れの解析です。このケースは橋梁柱周りの河川の流れに適用できますが、検証のためのベンチマークとして広く使用されているため、学術的な価値も大いにあります。

さらに、異なる問題構成における(渦の存在、サイズ、頻度に関連する)異なるレジームを示すためによく使用されます。

図3: 円柱軸に垂直な面(左)と平行な面(右)における速度の等高線プロット。左の図は、円柱を通過するカルマン渦の存在を示しています。

2つ目のケースは、ライダーを乗せたバイクの空力解析です(図4)。流速が速く、空気の粘性が低いため、乱流領域が発生しやすくなります。たとえ、車両後方の渦の剥離に関連する抗力を低減するために乱流が発生するのをできるだけ避けたとしても。

図4: バイク周囲の空気速度の等高線プロット。ヘルメットや車輪のスポークのような特徴は、乱流を大きく増加させ、その結果、空気抵抗を増加させます。

SimScaleでは、様々な乱流モデルを用いた熱流体解析を実施いただけます。

すぐにウェブブラウザで流体解析にトライ

参考

Richardson, L. F. Weather Prediction by Numerical Process (Cambridge Univ. Press, 1922)
https://micropore.wordpress.com/2010/08/21/kolmogorov-originl-paper-on-turbulence/
David C Wilcox et al. Turbulence modeling for CFD, volume 2. DCW industries La Canada, CA, 1998.
https://www.cfd-online.com/Wiki/Turbulence_modeling
M. Manhart. Turbulence modeling ss21, introduction to turbulence, 2021.

2024年4月8日

SimScale製品紹介資料ダウンロード

資料のサンプル

資料のサンプルはこちらからダウンロードできます。

資料請求

資料全体をご希望の方はこちらのフォームからお申し込みください。

カテゴリー: CAE Pedia

乱流とは

乱流の構造

最小乱流スケール

レイノルズ数

層流とは

レイノルズ数とは

境界条件とは