流体の流れは層流と乱流に分類されます。層流とは、流体が平行な層状に流れることで、層と層の間に乱れはありません。層流では、流体層は平行に滑り、流れに垂直な渦や渦巻き、流れはありません。

乱流とは

流体力学において乱流とは、渦や旋回、流れの不安定性が発生する不規則な流れを指します。乱流は、運動量の大きい対流と運動量の小さい拡散によって支配されます。層流と…

SimScale

このタイプの流れは、交差しない流線によって特徴づけられるため、流線流とも呼ばれます(図1)。つまり、すべての流体粒子は、その前の粒子と同じ軌跡をたどります。層流は、流体がゆっくりと、比較的小さな流路を、および／ま たは粘度が高い場合によく見られます。

層流は拡散が支配的であり、対流はあまり重要ではありません。より物理的な用語では、慣性力よりも粘性力の方が大きいことを意味します。

拡散/Fickの法則とは

フィックの法則は、高濃度領域から低濃度領域への粒子の移動を説明します。拡散として知られるこのプロセスは、圧力勾配による流れの動きであるバルクフローとは無関係に…

SimScale

粘性とは

粘性とは、運動や変形に対する流体の内部抵抗を測定する、流体の集中的な特性です。空気、水、油などの流体の流れの性質を決定するため、空気力学や貯留層工学などの分野…

SimScale

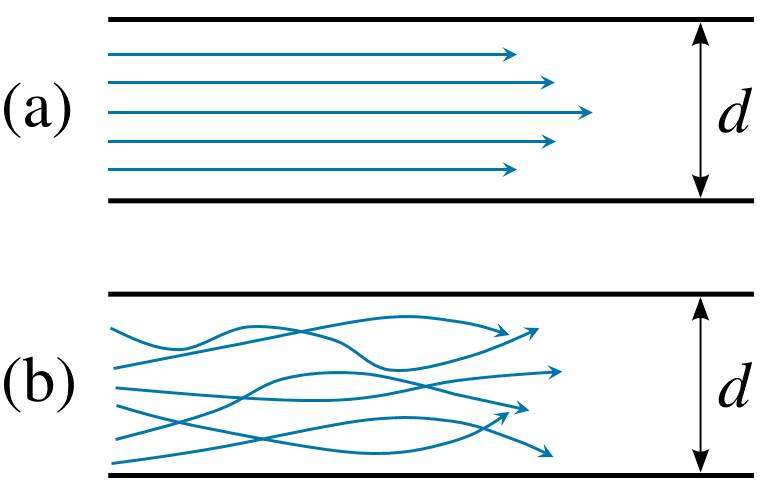
図1: (a) 閉鎖管内の層流、(b) 閉鎖管内の乱流

層流と乱流の比較

層流と乱流の区別は、19世紀後半にOsborne Reynoldsによって初めて研究・理論化されました。このトピックに関する彼の最初の出版物(\(^{1}\) )は、流体力学の研究における画期的な出来事と考えられています。

この研究は、レイノルズが層流領域から乱流領域への遷移を示すために使用した実験に基づいています。

この実験は、大きなガラス管内の水流の挙動を調べるというものでした。流れを可視化するため、レイノルズは小さな水脈を染めた水を流れに注入し、流速を変えてその挙動を観察しました。

• 流速が小さいと、染まった層はパイプの全長にわたって明瞭なままでした。
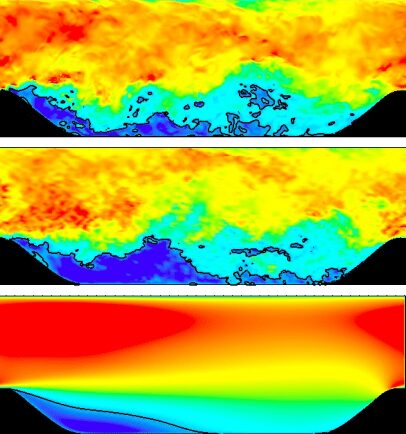
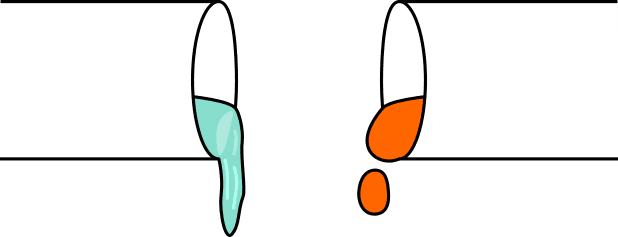
• 流速を上げると、図2に示すように、水脈は分断され、管の断面全体に拡散しました。

こうしてレイノルズは、層流と乱流と呼ばれる、遷移相を隔てた2つの異なる流れ場が存在することを実証しました。レイノルズはまた、この遷移の発生に影響する多くの要因を特定しました。

図2: レイノルズによる遷移相の実験観察。流線型の染料が徐々に渦や渦巻きに移行する様子。

レイノルズ数

レイノルズ数(Re)は、慣性力と粘性力の比を表す無次元数。1851年にジョージ・ガブリエル・ストークスが初めてこの概念を導入しましたが、オズボーン・レイノルズが普及させ、層流と乱流の遷移を識別するパラメータとして提唱しました。そのため、無次元数はレイノルズ数となり、1908年にアーノルド・ゾンマーフェルドがオズボーン・レイノルズにちなんで命名しました\(^2\) 。

レイノルズ数は、大域的な流れの巨視的パラメータであり、数学的には次のように定義されます:

$$ Re=\frac{\rho u d}{\mu} =\frac{ud}{\nu} \tag{1}$$

ここで

• \(\rho\) は流体の密度
• \(u\) は流体の巨視的速度
• \(d\) は特性長(または水力直径)
• \(\mu\) は流体の粘度
• \(\nu\) は流体の動粘度

レイノルズ数とは

無次元数の一つであるレイノルズ数は、流体の挙動パターンを予測する上で重要な役割を果たします。レイノルズ数は、流体の流れが層流か乱流かを決定するために使用されま…

SimScale

流体の流れとレイノルズ数の値

レイノルズ数が低い場合、流れは層流です。レイノルズ数が閾値を超えると、流れに半発達乱流が発生します。この領域は通常「遷移領域」と呼ばれ、レイノルズ数の特定の範囲で発生します。その範囲を超えると、流れは完全に乱流になります。

遷移領域におけるレイノルズ数の平均値は、通常「臨界レイノルズ数」と呼ばれます。これは層流と乱流の間の閾値です。

レイノルズ数が流体の材料特性とアプリケーションの幾何学的特性の両方に依存することは興味深いことです。これは主に2つの結果をもたらします:

• レイノルズ数は、局所的な挙動ではなく、流れの大域的な挙動を記述します。大きな領域では、領域全体に広がらない局所的な乱流領域が存在する可能性があります。このため、正確な適用領域と特性長を決定するには、流れの物理を理解することが重要です。
• レイノルズ数は適用体系ごとの特性です。同じ適用先でも構成が異なれば、臨界レイノルズ数も異なります。

次の表は、さまざまな問題で得られたレイノルズ数と領域の対応を示しています。

層流と乱流の遷移領域

層流と乱流を分ける遷移領域は、層流と乱流が同じ流れの中で同居するレイノルズ数の範囲で発生します。これは、レイノルズ数が乱流の大域的な推定値であり、流れを局所的に特徴付けるものではないからです。実際には、他のパラメータが局所的に流れに影響を与える可能性があります。

例えば、ムーディー線図(図3)を用いて解析的に研究された閉管内の流れがあります。流れの挙動(摩擦係数で記述)は、レイノルズ数と相対粗さ\(^3\) の両方に依存します。相対粗度は「局所的な」因子であり、境界に近接しているために異なる挙動を示す領域の存在を示します。

• 左側に示されているように、層流領域は線形で粗さに依存しません。
• 完全な乱流はグラフの右側(曲線が平坦なところ)にあり、高いレイノルズ数および／または高い粗さの値で発生し、流れに摂動を与えます。
• 最も興味深いのは中央の遷移領域で、この領域では摩擦係数がレイノルズ数と相対粗さの両方に大きく依存します。また、乱流領域の始まりの記述は、その偶発的な性質のために信頼できません。

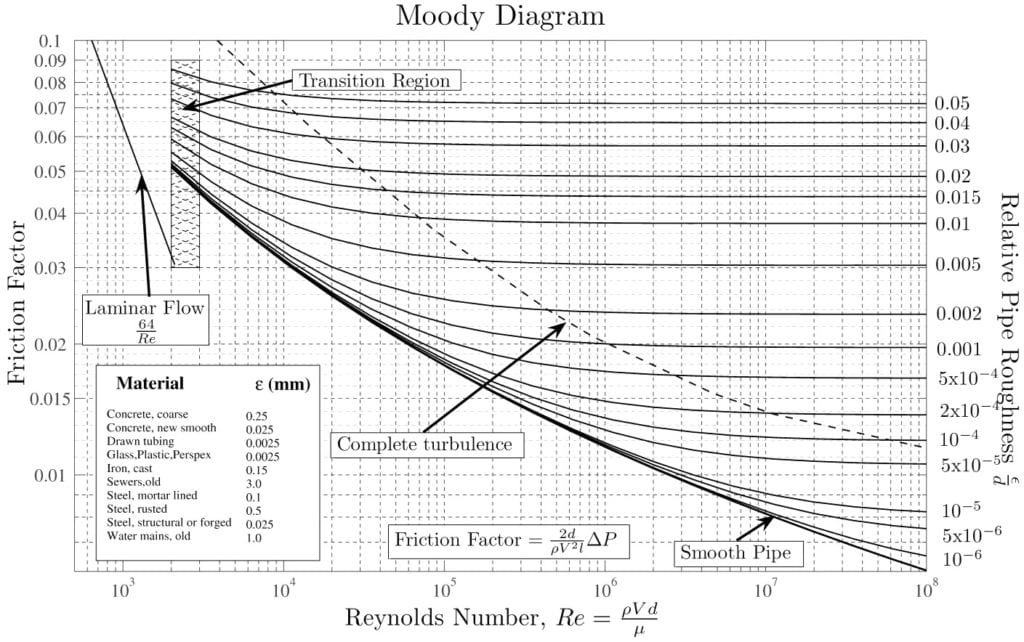
図3: 流れ領域を区別するムーディー線図

層流の応用

層流は学術的にも工業的にも応用されています。

層流領域の多くの流れは、高度なシミュレーショ ン技術を開発するためのベンチマークとして利用されてい ます。これは、図 4(a)に示す「蓋駆動キャビティ」\(^4\) の場合であり、臨界レイノルズ数は\(Re=1000\) です。結果として得られる速度場(図 4(b))はレイノルズ数に依存し、主な流れの特性(渦の数、渦の中心位置、速度プロファイルなど)は広範にベンチマークされています。

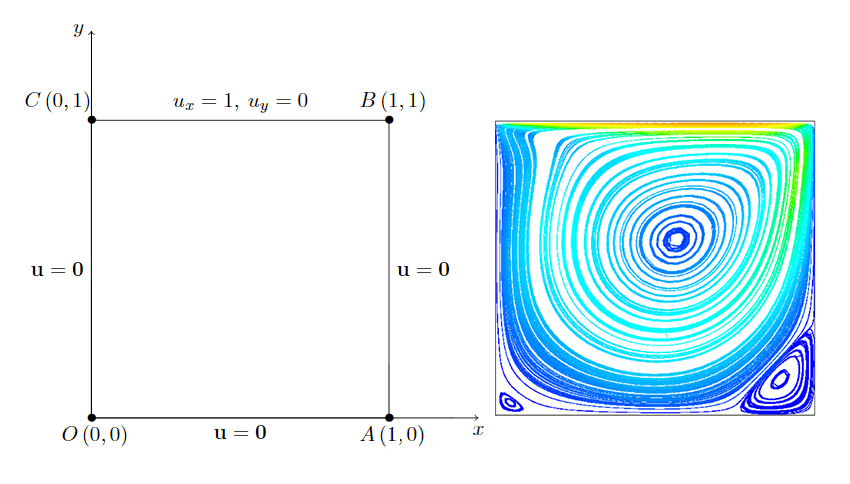
図4: 蓋駆動空洞: (a) 形状と境界条件(u=0は壁を表す); (b) Re=500の場合の流速線。上部(赤)で高い流速を示し、壁近傍(青)ではほぼゼロ流速。

工業的な観点からは、層流領域は通常、低流速、低密度、高粘度の流れで発達します。これは通常、自然対流(図5)や低流速で作動する換気システム(図6)の場合です。

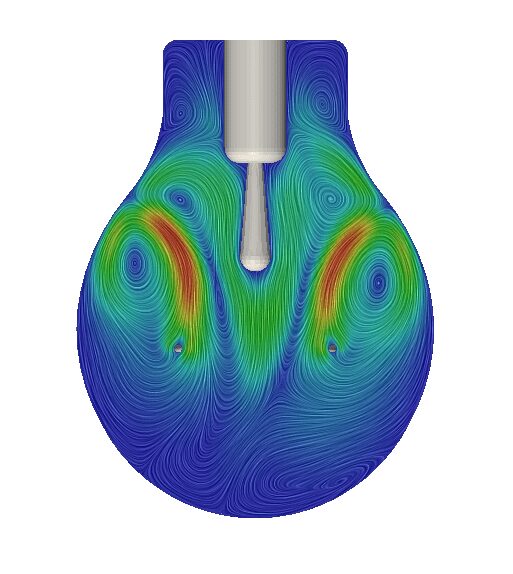
図5: 温度差が層流を制御するバルブ内の自然対流。

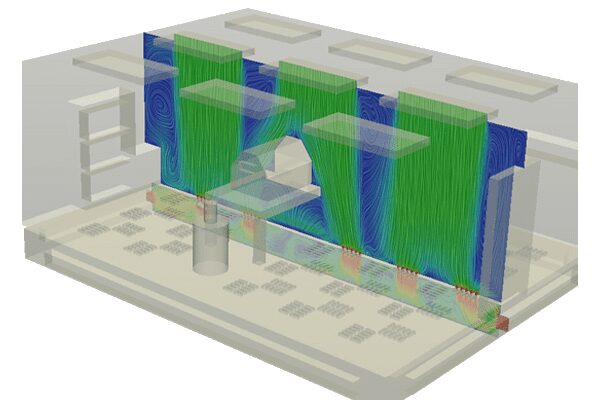
図6: クリーンルーム内の換気システム。温度差に支配された低流速の流れには、滑らかな連続流線が観察されます。

参考

1. “An experimental investigation of the circumstances which determine whether the motion of water shall be direct or sinuous, and of the law of resistance in parallel channels”. Proceedings of the Royal Society of London. 35 (224-226): 84–99
2. “Arnold Sommerfeld: Science, Life and Turbulent Times 1868-1951”, Michael Eckert. Springer Science Business Media, 24 giu 2013.
3. Moody, L. F. (1944), “Friction factors for pipe flow”, Transactions of the ASME, 66 (8): 671–684
4. C.T. Shin U. Ghia, K.N. Ghia. High-Resolution for incompressible flow using the Navier-Stokes equations and the multigrid method. J. Comput. Phys., 48:387–411, 1982.