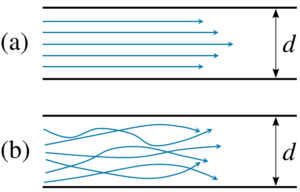
ブシネスク近似は、浮力によって駆動される流れを解くために使用され、ナビエ・ストークス方程式の完全な圧縮性定式化を解くよりも、計算コストが低くなります。
ブシネスク近似はすべての非等温流に適用可能であり、重力が乗算される方程式項を除いて密度差を無視します。
これにより、慣性効果による密度差は完全に無視され、密度は温度のみの関数となります。また、ブシネスク近似では一定の動粘性を仮定しており、乱流と層流の両方に使用できます。
この近似は、温度に依存する密度の線形変化を仮定しています。とくに、周囲との温度差が比較的小さい自然対流の流れに対しては非常に正確です。
そのため、比較的低温である電子機器の冷却、建物の空調、および熱的快適性の評価などに適しています。
一方で、流れが高速 (およそ 120 m/s 以上) または高温 (100 °C 以上) になると、温度と密度の間の線形仮定が成立しなくなるため、ブシネスク近似の精度は低下します。
CFDにおけるブシネスク近似
ブシネスク近似は、計算流体力学 (CFD) の黎明期において、優れた密度近似を可能にしながら、計算コストを削減できるという理由で人気を博しました。
商用CFDがまだ黎明期であった1980年代には、計算能力も現在の数分の一にすぎませんでした。ブシネスク近似を使用することで、計算の高速化を達成することができたのです。
その後、過去数十年にわたって計算能力が大幅に向上したことにより、ブシネスク近似の必要性は徐々に低下しました。しかし、現在でも多くの商用CFDコードにおいて利用されています。
ブシネスク近似理論
ブシネスク近似では、密度の変動は参照密度、温度、および熱膨張係数の関数として表されます。
$$ \rho = \rho_0 – \alpha \rho_0(T-T_0) $$
ここで:
- \(\rho\): 局所密度
- \(\rho_0\): 参照密度
- \(\alpha\): 熱膨張係数
- \(T\): 局所温度
- \(T_0\): 参照温度
SimScaleでのブシネスク近似
SimScaleでは、以下の値を用いて空気の物性値を近似しています:
- \(\rho_0 = 1.196 kg/m^3\)
- \(\alpha= 0.00343 1/K\)
- \(T_0 = 295.15 K\)
したがって、ブシネスク近似に基づく密度の式は次のようになります:
$$ \rho = (1.196 kg/m^3) – (0.00343 1/k) \times (1.196 kg/m^3) \times (T-295.15 K) $$
このように、密度を温度の関数としてプロットし、実際の密度との比較を行うことで、一般的な温度範囲における相関関係を可視化・理解することができます。
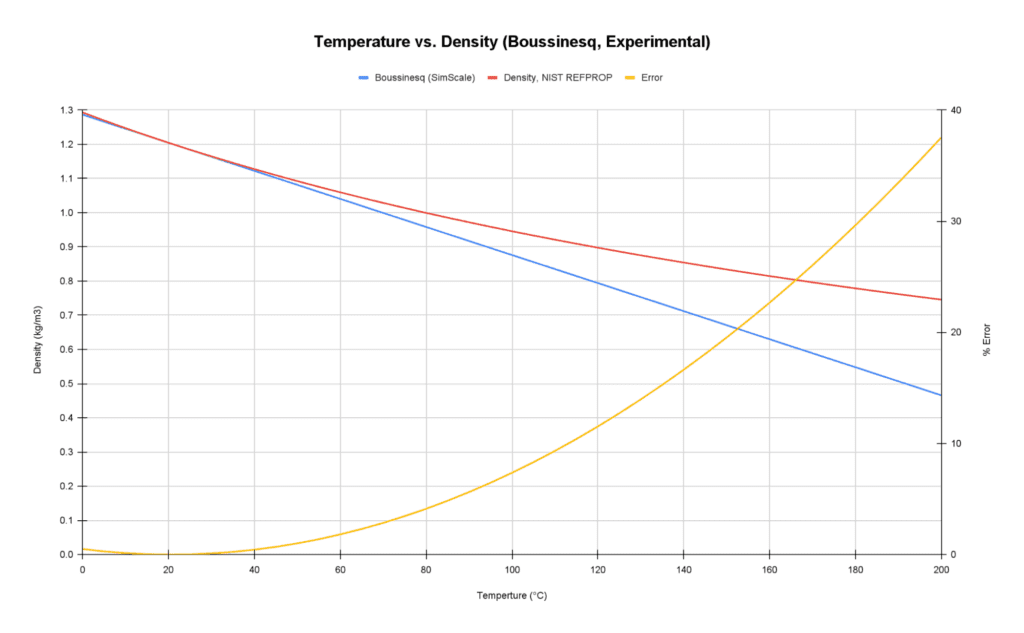
図1: 密度対温度をプロットして、ブシネスク近似と実験値の比較を示すグラフ
115 °Cまでは、実験空気密度とブシネスク近似による密度の誤差が10%未満であることがわかります。
そのため、115 °Cを超える可能性のあるシミュレーションでは、圧縮性流れのモデルを使用することを推奨します。
こうすることで、空気を理想気体としてモデル化できます。理想気体の法則は、より高温・高圧の範囲において有効です。
例: 電子基板の熱管理
SimScaleのチュートリアル「電子基板の熱管理」では、圧縮性流体ソルバーを用いて、理想気体の状態方程式に則った計算が行われています。
本記事では、ブシネスク近似が結果にどのような影響を与えるかを理解するため、非圧縮性流体ソルバーとブシネスク近似機能を用いた計算を実施しました。

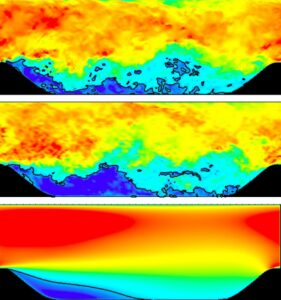
図2: (ブシネスク近似不使用)流体の圧縮性を考慮した計算結果

図3: ブシネスク近似を使用した計算結果
流体の圧縮性を考慮した計算結果とブシネスク近似を使用したシミュレーション結果を比較すると、結果はほとんど同等であることわかります。メインボードの大型チップ の平均温度は、圧縮性ソルバーでは 59.6℃、ブシネスク近似では 58.6℃でした。同様に、ドメイン内の最高温度は、圧縮性ソルバーでは97.3 °C、ブシネスク近似では95.2 °Cです。
ブシネスク近似と合わせて読みたい記事
SimScale製品紹介資料ダウンロード

SimScaleの特徴と計算事例をまとめた資料を用意しております。