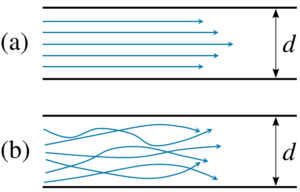
この記事では、圧縮性流れと非圧縮性流れの違いを探ります。その前に、流れとは何でしょうか？

流れとは、単位時間あたりにある点を通過する流体(液体、蒸気、気体)の動きのことです。流体の流れは、流体力学の一部です。この動きは、さまざまな不均衡な力の結果であり、加えられた力のバランスが取れるまで続きます。簡単な例は、重力によって高さから落下する滝です。

アニメーション1: 多相シミュレーションを使用した運河の放水路

流れの種類

流体力学では、流れはその性質に基づいてさまざまなカテゴリに分類することができます。流体の流れには次のような種類があります:

定常と非定常
均一と不均一
層流と乱流
圧縮性と非圧縮性
回転と非回転

ここでは、圧縮性流れと非圧縮性流れの違いに焦点を当てます。

圧縮性流れと非圧縮性流れの違い

圧縮性流れでは、流体の密度は一定ではありません。

$$ \rho \neq constant \tag{1}$$

一方、非圧縮性流れとは、流体の密度が一定である流れを指します。

$$ \rho = constant \tag{2}$$

したがって、材料力学の用語では、粘性や外力によって非圧縮性流体にせん断力が加わっても、流動中に密度が変化することはありません。

アニメーション2: 建物周囲の非圧縮性気流

圧縮性とマッハ数

流体は柔軟な構造をしているため、流体粒子の圧縮性は重要な問題です。実際には、すべての流体はもともと圧縮性です。分子構造のさまざまな範囲において、あらゆる種類の流体が圧縮性であるにもかかわらず、密度の変化が無視できるため、ほとんどの流体は非圧縮性であると仮定することができます。

しかし、流速が臨界値を超えるような高速の流れは、非圧縮性と仮定することはできません。これはマッハ数によって決まります。マッハ数は、流速を周囲の媒体の音速と比較する無次元数です。次のように計算されます:

$$ Ma=\frac{V}{a}\ \tag{3}$$

ここで、$Ma$ はマッハ数、$V$ は流速、$a$ は流体中の音速で、その温度の関数です。

マッハ数が0.3未満の場合、流れは非圧縮性であると考えられます。
マッハ数が0.3より大きい場合、すなわち高速流の場合、密度の変化は無視できず、流れは圧縮性と見なされます。

20$°C$ と 1$atm$ (101,325$Pa$) の空気では、音速は約 340$m/s$ です。したがって、マッハ数0.3は約100$m/s$ の流速に相当します。例えば、自動車の速度が100$m/s$ よりも大きい場合、信頼性の高い数値解析を行うのに適したアプローチは圧縮性流れです。

図1: ノズル内の衝撃波

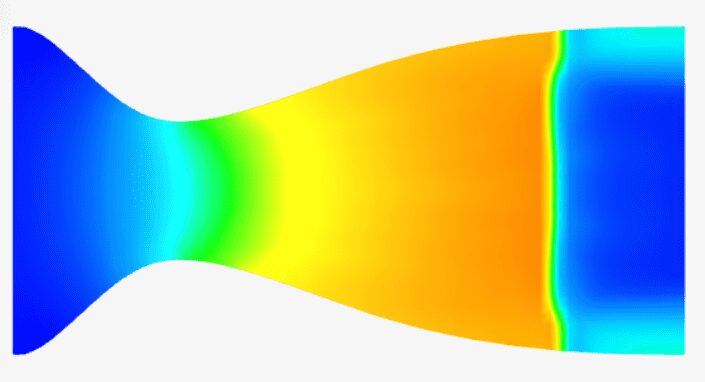
流れを分類する基準としての密度

圧縮性流れと非圧縮性流れを分類する一般的な基準は、密度の変化が5%以下の場合、その流れは非圧縮性とみなされます。密度の変化が5%より大きい場合、その流れは圧縮性です。密度の変化が5%ということは、マッハ数が約0.3に相当します。

密度変化の基準限界は任意です。閾値を厳密に1%に設定した場合、マッハ数はおおよそ0.14となり、流速は約50$m/s$ となります。流速が同じでも、音速は温度や圧力によって変化するため、マッハ数が変化する可能性があることに留意してください。

一方、水のような液体の密度はほとんど変化しません。水の音速は気体の音速よりも速い。例えば、水中での音の伝搬は、20$°C$ と 1$atm$ で約 1481$m/s$ です。その結果、液体は一般に非圧縮性流体と呼ばれます。

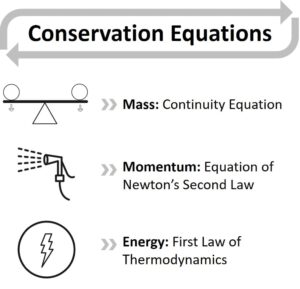
圧縮性流れと非圧縮性流れの支配方程式

流体の流れを支配する方程式は、流体の物理的性質の保存則に基づいています。基本方程式は、以下の3法則¹からなります:

質量保存連続方程式
運動量保存則: ナビエ・ストークス方程式
エネルギー保存: 熱力学第一法則またはエネルギー方程式

連続の式

質量保存の方程式は次のように規定されます:

$$ \frac{D\rho}{Dt} +\rho (\nabla \cdot \vec{v}) =0 \tag{4}$$

ここで、$\rho$ は密度、$\vec{v}$ は速度、$\nabla$ は勾配演算子です。

$$ \vec{\nabla} = \vec{i} \frac{\partial}{\partial x} + \vec{j} \frac{\partial}{\partial y} + \vec{k} \frac{\partial}{\partial z} \tag{5}$$

密度が一定である非圧縮性流体の場合、連続方程式は次のようになります:

$$ \frac{D\rho}{Dt} = 0 \rightarrow \nabla \cdot \vec{v} = \frac{\partial u}{\partial x} + \frac{\partial v}{\partial y} + \frac{\partial w}{\partial z} = 0 \tag{6}$$

図2: 質量、運動量、エネルギーの保存方程式

ナビエ・ストークス方程式

ナビエ・ストークス方程式と呼ばれる運動量保存方程式は、次式で与えられます:

$$ \overbrace{\frac{\partial}{\partial t} (\rho \vec{v})}^{I} + \overbrace{\nabla \cdot (\rho \vec{v} \vec{v})}^{II}= \overbrace{-\nabla p}^{III} + \overbrace{\nabla \cdot \left(\overline{\overline{\tau}}\right)}^{IV} + \overbrace{\rho \vec{g}}^{V} \tag{7}$$

ここで、$p$ は静圧、$\overline{\overline{\tau}}$ は粘性応力テンソル、$\rho \vec{g}$ は単位体積あたりの重力。ここで、ローマ数字は

I: 時間による局所変化
II: 運動量対流
III: 表面力
IV: 拡散項
V: 質量力

を示します。

粘性応力テンソル$\overline{\overline{\tau}}$ は、ストークの仮説に従って以下のように指定できます:

$$ \tau_{ij} = \mu \frac{\partial v_i}{\partial x_j} + \frac{\partial v_j}{\partial x_i} – \frac{2}{3}(\nabla \cdot \vec{v}) \delta_{ij} \tag{8}$$

流体が一定の粘性係数$\mu$ を持つ非圧縮性であると仮定すると、ナビエ・ストークス方程式は次のように簡略化されます:

$$ \rho \frac{D\vec{v}}{Dt} = -\nabla p + \mu \nabla^2 \vec{v} + \rho \vec{g} \tag{9}$$

エネルギー方程式

質量保存方程式と運動量方程式だけでは、流体の流れを表現するには不十分です。熱力学のエンタルピー方程式を追加する必要があります。この方程式には散逸項が含まれ、熱やその他のエネルギー交換が関与する場合には、流れの間の温度変化を考慮します。

対流および共役伝熱シミュレーションでは、正確な CFD 解析を行うために熱エネルギーの移動が伴います。圧縮性流体の応力-ひずみ関係は、圧縮性流体の方程式をさらに複雑にします。

支配方程式の詳細については、以下の記事をご覧ください:

アプリケーション

非圧縮性流れ

非圧縮流れモデリングは、CFDの多くのアプリケーションに使用されています。以下に一般的なアプリケーションを示します:

バルブや水車を通過する流れ

図3: グローブバルブの流線図

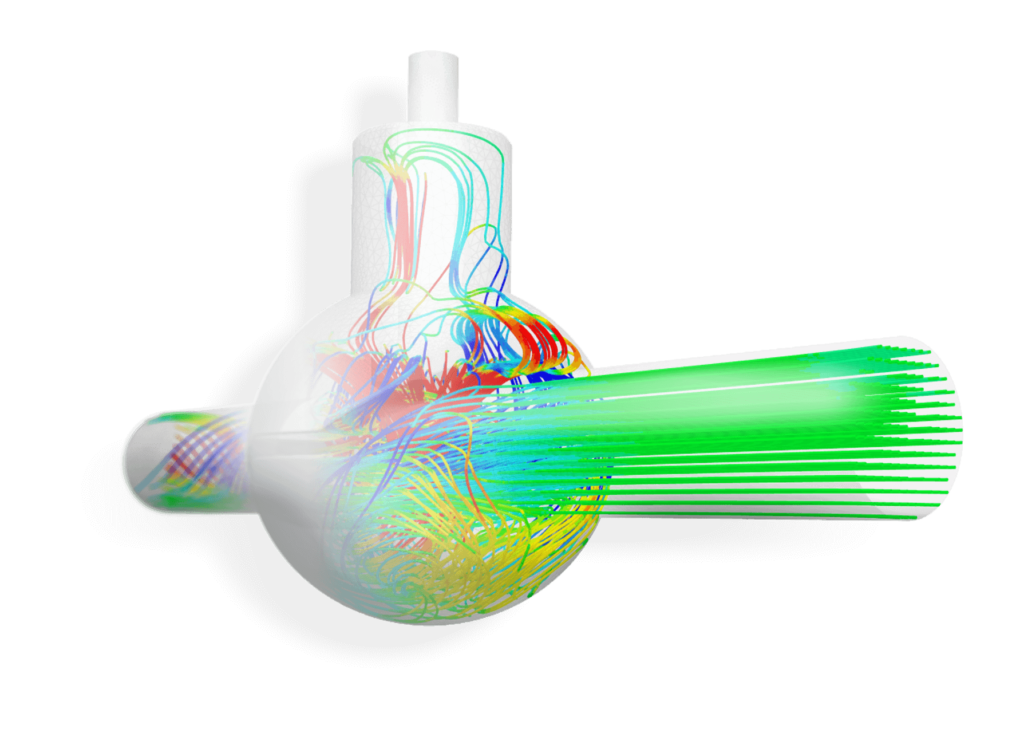
様々な流量の入口と出口の圧力差を理解することで、最高の効率を得るための最適な作業条件を提供することができます。これは、カジュアルティの寿命を延ばすのに役立ちます。

駐車場の換気

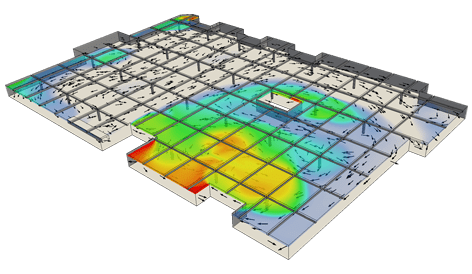
図4: SimScaleを使用したパッシブスカラーによる駐車場の換気シミュレーション

駐車場はピーク時にはかなり混雑するため、換気扇のようなHVACシステムの存在が重要になります。CFDシミュレーションにより、車から出る煙のような受動的なエンティティを検出し、追跡することで、このような混雑した空間における安全基準を把握することができます。

車両の空気力学

図5: SimScaleでの学生フォーミュラカーの空力解析

非圧縮流れ解析は，マッハ数が低い車両の空力/流体力学($Ma$ < 0.3)では極めて一般的です．また，フォーミュラ 1 レース(F1)の空気力学のような極端なケースでは，圧縮性を考慮するほど速度が高くありません(F1 の記録速度は 372.5$km/h$ 10 であり，$T$= 40$°C$ で$Ma$ = 0.29 に相当します)．

圧縮性流れ

高速流や大きな圧力差を伴う流れを含む多くの工学的用途は、本質的に圧縮性です。

航空機の翼解析

図 6: 圧力の可視化により、揚力を発生させる分布の違いが明らかに

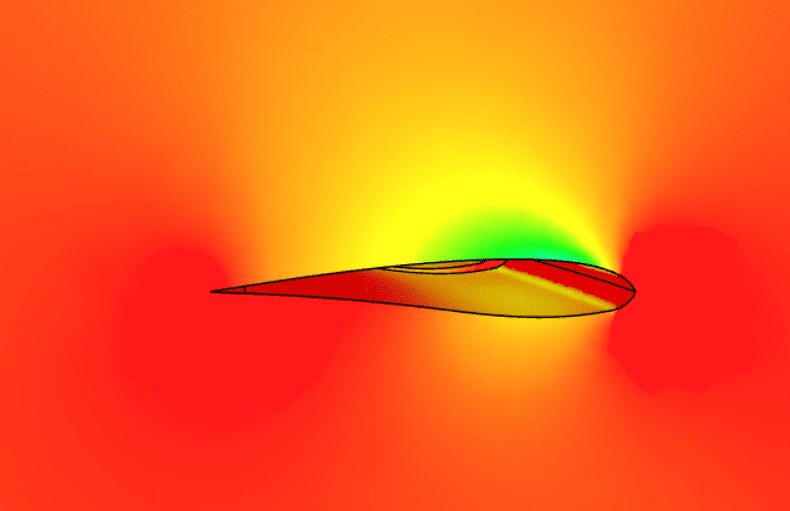
ほとんどの民間航空会社は、圧縮性解析の範疇である 0.6～0.9 マッハの速度範囲で飛行しています。翼の周囲に発生する乱流と渦を正確に予測する CFD シミュレーションによって、翼設計の空力学的開発が促進されます。

超音速域(1.2～5マッハ)や極超音速域(5～10マッハ)では衝撃が発生しますが、この衝撃も圧縮性流体解析を使用してシミュレーションで捉えることができます。

ガスタービンと蒸気タービン

図7: 流線によるタービンのシミュレーション

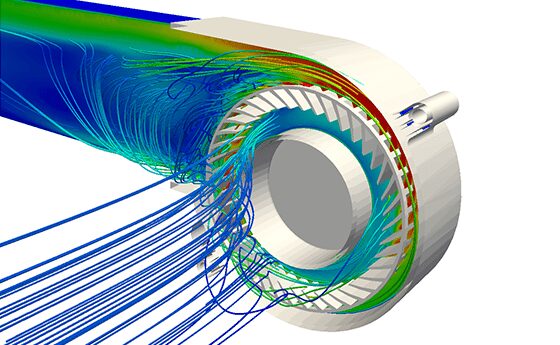
メーカー/科学者は、静圧、所要動力、回転速度、および流量あたりの効率値の条件間の関係を記述したターボ機械のデータ曲線を提供しています。回転部品の設計のための実験試験は非常に複雑で高価であるため、シミュレーションデータは、エンジニアが設計プロセスの初期段階で、高圧や高温の状況に実際に対処することなく、所望の流量/冷却条件を達成するなどの意思決定を行うために必要です。

内燃エンジン

図 8: ベクトルマッピングによる内燃エンジンのシミュレーション

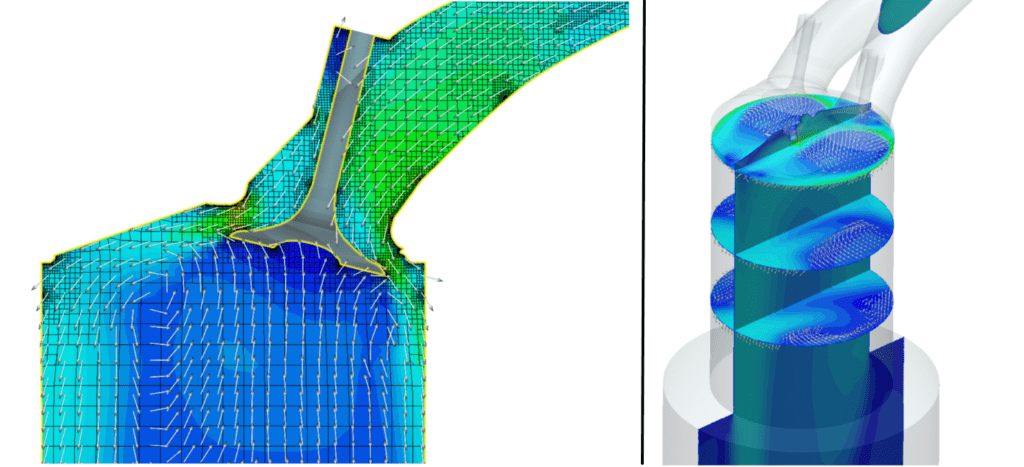
エンジンの CFD モデリングは、新しい燃料と空気吸入口の燃焼を評価し、より低い解析コストで排出量を削減することができます。現代の内燃(IC)エンジンの開発は、CFD シミュレーションによってエンジン技術のさらなる進歩を示唆することができるため、CFD シミュレーションに依存しています。

さらに、高温や高圧などの要因によって計測に問題がある状況や場所でも、シミュレーションを使用して流れを調べることができます。

参考

Frank M. White, Viscous Fluid Flow, McGraw-Hill Mechanical Engineering, 3rd Edition, ISBN-10: 0072402318

2024年3月13日

SimScale製品紹介資料ダウンロード

SimScaleの特徴と計算事例、プランと価格をまとめた資料を用意しております。

資料を請求する

お問い合わせ（デモや製品紹介はこちらから）

カテゴリー: CAE Pedia

圧縮性流れと非圧縮性流れ