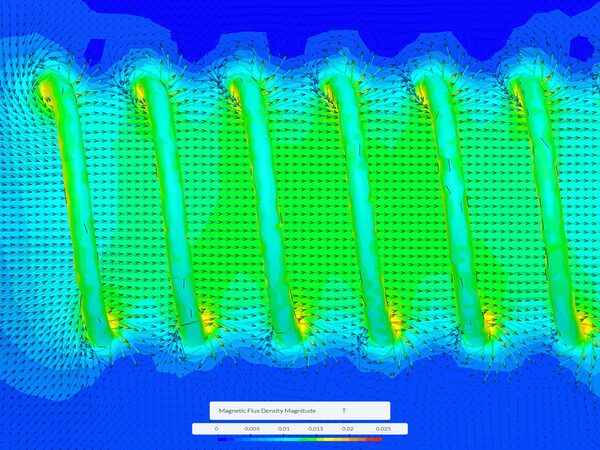
ジュール熱とは、導体に電流が流れることで発生する熱エネルギーのことです。この現象は、電流によるエネルギー損失が熱に替わる物理的効果であり、導体の温度上昇として確認されるため、「加熱現象」とも呼ばれます。
ジュール熱は、電気エネルギーが熱エネルギーに変換されるプロセスであり、エネルギー保存則に従う変換の一例とみなすことができます。
ジュール加熱 (ジュール効果) の歴史
ジュールと加熱効果の発見
ジュール熱の発見は、1840年ころ、イギリスのアマチュア科学者ジェームズ・プレスコット・ジュールによって研究され、初めて定式化されました。
ジュールは、実家の醸造所を経営しながら、当時発明されたばかりの電気モーターに注目していました。彼はこれが、醸造工程で使われていた蒸気機関よりも経済的かどうかを調べようとしました。しかし、電気モーターは亜鉛電池によって電力を供給する必要があり、結局は蒸気機関ほどのコスト効率は得られないことが分かりました。
この調査をきっかけに、ジュールはエネルギー生成・伝達・変換についての研究を本格化させます。数々の実験の成果は、のちに熱力学第一法則 (エネルギー保存則) の確立につながりました。また、エネルギーのSI単位「ジュール (J)」は、彼の業績を記念して命名されました\(^1\)
水中での電流加熱実験
ジュールの実験のひとつに、電流が流れる導体の加熱効果に関する研究がありました。
彼は、水に浸した導線を電池に接続し、電流を流した際の水温の上昇を記録しました。この実験から得られたデータを分析した結果、以下のような関係式が導かれました:
$$\frac {H}{t} = I^2R \tag{1}$$
パラメータ:
- \(H\): 発生した熱量 [\(J\)]
- \(t\): 時間 [\(s\)]
- \(I\): 電流 [\(A\)]
- \(t\): 電気抵抗 ]\(\omega\)]
これは現在「ジュールの第一法則」として知られており、「導体に流れる電流によって発生する単位時間あたりの熱量は、電流の二乗と抵抗に比例する」という法則です。
発生電力としての表現
今日では、この関係式は発生電力\(P\)を使って以下のように書かれることが一般的です:
$$\frac {H}{t} = P = I^2R \tag{2}$$
この式は、導体内で消費される電気エネルギーが熱に変換される様子を簡潔に表したものであり、ジュール熱の基本的な物理的理解に役立ちます。
ジュール効果の仕組み
ジュールの発見によって、電流が流れると導体に熱が発生することが明らかになりました。
電流と電圧の関係
そもそも電流とは、電子が物質内を移動する流れです。この電子の流れを引き起こすのが、電圧 (電位差) です。
電圧とは、物質中の2点間に生じる電気的な高低差であり、電子を「押し出す力」のようなものです。ただし、電子が実際に移動するかどうかは、以下のような要因によって決まります:
- 自由電子の有無 (=電子が動ける材料かどうか)
- 電子の移動のしやすさ (=電気抵抗)
- 電圧の大きさ
この関係を表すのが、オームの法則です:
$$I = \frac {V}{R} \tag {3}$$
この式は、電流 \(I\) (単位時間あたりに流れる電荷量) は、電圧 \(V\) に比例し、抵抗 \(R\) に反比例することを示しています。
抵抗とは何か
抵抗 \(R\) とは、電流の流れにくさを表す値です。抵抗が大きいほど、同じ電圧でも電流はながれにくくなります。
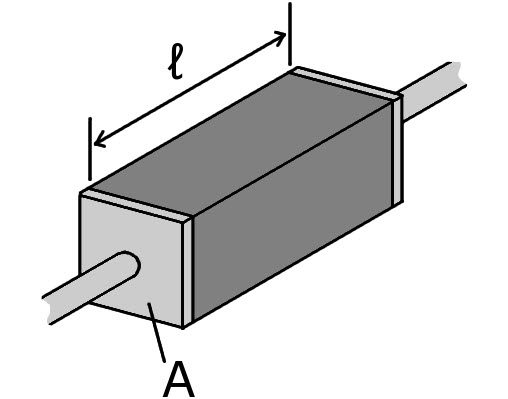
実験により、抵抗は導体の材料特性だけでなく、形状 (長さや断面積) にも依存することが分かっています。そのため、抵抗は次のように表されます:
$$R = \frac {\rho l}{A} \tag {4}$$
ここで:
- \(\rho\): 導体材料の抵抗率 (固有の性質)
- \(l\): 電圧がかかる導体の長さ
- \(A\): 導体の断面積
この式からもわかるように、導体が長いほど電流は流れにくく、太いほど流れやすくなります。
ジュール熱と電気抵抗の関係
すべての材料は、程度の差はあれど電流の流れに対して何らかの抵抗を示します。
その中でも、電気抵抗がゼロ (または極めて小さい) 特別な物質は「超伝導体」と呼ばれます。
代表的な材料の電気抵抗値は、こちらのリンク\(^3\)で確認できます。
ジュール熱と抵抗の関係
ジュールの法則に立ち返ると、その答えが見えてきます。
$$P=I^2R$$
この式からわかる通り、同じ電流 \(I\) が流れていても、抵抗\(R\) が大きいほど発生する熱 \(P\) も大きくなります。つまり、材料中を電子が移動しにくいほど、電子を「押し進める」ためにより多くのエネルギー (仕事) が必要になり、そのエネルギーが熱として材料に蓄積されるのです。
ここで言う「熱に変換される」は、途中で他のエネルギー形態に逃げることなく、ほぼすべてが熱として消費されるという意味で「直接的」と表現されます。
ジュール熱の計算方法
電機導体の加熱と電力損失
長さ\(l\) 、断面積\(A\) 、抵抗率\(\rho\) を持つ材料でできた電気導体(電線、棒、板など)に対しては、以下の式から電気抵抗\(R\)を計算することができます。
$$R = \frac {\rho\ l}{A} \tag {4}$$
この導体の両端に電位差\(V\) (直流) を加えると、オームの法則により、電流\(I\) が次のように流れます:
$$I = \frac {V}{R} \tag {3}$$
このとき導体内で発生し、熱として失われる電力\(P\)は、ジュールの法則に従い以下のように表されます:
$$P = I^2R \tag{2}$$
この電力が時間\(t\)にわたって継続して加わることで、導体に蓄積される熱量\(Q\)は次のように計算できます:
$$Q=Pt \tag {5}$$
さらに、この熱量によって導体の温度がどれだけ上昇するかは、比熱\(c\)と質量\(m\)を用いて以下の式で求められます:
$$T = \frac {Q}{cm} \tag {6}$$
ここでは、導体の形状や物性値が全長にわたって一定であり、すべての量が同一の単位系で定義されていると仮定しています。
交流電流 (AC) の場合
交流電流を流す場合、上記の式は瞬時値に基づくものであり、熱の蓄積量などを正しく表すことはできません。これを補うためには、二乗平均平方根 (RMS) を用いた評価が必要です。
電流、電圧、および電力のRMS値は次のように定義されます:
$$I_{RMS}=V_{RMS}R \tag {7}$$
$$P = P_{RMS}=I_{RMS}^2R \tag {8}$$
このように、交流でもジュール損失 (熱の発生) はRMS値を使えば直流と同様に扱うことができます。
ジュール加熱の応用
ジュール加熱 (導体に電流を流すことで発生する熱) は、私たちの生活のあらゆる場面で利用されています。家庭、輸送、工業製品など、多岐にわたる用途があります。
抵抗加熱 (直接加熱・熱放射)
導体に電流を流して発熱させ、直接加熱したり、熱放射・対流で周囲を温める方式です。
- 白熱電球: フィラメント (抵抗体) に電流を流し、発熱・発光。
- オーブン/トースター: 内部の抵抗体を熱源として食品を加熱。
- 電機のストーブ・ホットプレート: 加熱面に鍋や調理器具を直接置いて使用。
- 車のフロントガラスヒーター: 抵抗線でガラス面を温め、曇りや凍結を防止。
- コーヒーメーカー: 沸騰と保温を2段階で制御する抵抗加熱。
誘導加熱 (電磁誘導によるジュール加熱)
誘導加熱は、導体に直接電流を流すのではなく、電磁誘導 (磁場変化により内部に電流を誘導) して加熱させる方法です。
- IHクッキングヒーター: 鍋に電流を誘導し、鍋自体を加熱。
- 工業用誘導加熱炉: 金属の焼き入れや溶解処理に利用。
- 鉱物用誘導炉: 金属を高効率で溶解。

電気暖房の応用について語る際、最も重要な観点の一つが「エネルギー効率」です。
先に述べたように、導体に電流を流して熱を発生させるプロセス (ジュール加熱) は、エネルギー損失がほとんどありません。電気エネルギーは、ほぼ100%の効率で熱に変換されます。これはエネルギー変換の中でも極めて優れた特性です。
しかし、この発生した熱を「どのように利用するか」という点に目を向けると、話は変わってきます。熱の利用には以下のような方法があります:
これらの熱伝達プロセスでは、どうしても環境への放熱や損失が避けられません。そのため、最終的な熱の利用効率は大きく低下する傾向があります。
つまり、消費された電力に対して、実際に有効に使われるエネルギーの割合が低いということです。その結果、エネルギーの浪費が生じ、環境への負荷が大きくなる点が問題視されます。
たとえば、白熱電球と比べてLED電球は、同じ明るさを得るのに必要な電力が約5分の1とされています。これは、白熱電球の多くのエネルギーが光ではなく、熱として失われているためです。
参考
- “APS NEWS: December 1840: Joule’s abstract on converting mechanical power into heat.”
- “Thinktank, Birmingham Science Museum / CC BY-SA (https://creativecommons.org/licenses/by-sa/4.0)”
- “ThoughtCo. Table of Electrical Resistivity and Conductivity.”
- “Wikipedia. Root mean square.”
- “Wikimedia commons. Resistivity geometry.”
- “The Lightbulb Company. LED Lumens To Watts Conversion Chart.”
SimScale製品紹介資料ダウンロード

SimScaleの特徴と計算事例をまとめた資料を用意しております。