曲げ応力は、固体力学および構造解析において極めて重要な概念です。そびえ立つ超高層ビルから最小の機械部品に至るまで、あらゆる構造物は様々な部品から構成されており、それらが構造物の荷重に対する耐力と変形に対する抵抗力を高めています。

この中で、曲げ応力は、特に梁のような要素が荷重を受けて曲がるシナリオにおいて、極めて重要な側面として際立っています。そのため、特に曲げ応力とそれに関連する法線応力が構造体に与える影響という点で、材料の力学と異なる材料が応力下でどのように反応するかを十分に理解することが不可欠です。

この記事では、曲げ応力とは何か、どのように計算されるのか、梁の曲げのような特殊なケースにどのように適用されるのかについて説明します。また、様々な状況における曲げ応力を可視化し、より深く理解するためのシミュレーション解析の役割についても説明します。

曲げ応力の定義

曲げ応力とは、外部からの曲げモーメントまたは力が加えられたときに、コンポーネント内で発生する内部抵抗のことです。この曲げモーメントはコンポーネントに曲率をもたらし、曲げ応力と総称される引張応力と圧縮応力を発生させます。

曲げ応力の背後にある理論には、平面断面の仮定と線形弾性材料の挙動という2つの重要な仮定があります。

平面断面の仮定は、構造物のどの断面も曲げ後も平面のままであることを示唆します。
線形弾性材料の挙動は、法線応力がひずみに正比例することを前提としており、この関係はフックの法則として知られています。

例えば、梁の曲げ応力は断面全体に一様に分布するわけではありません。例えば、梁の曲げ応力は断面全体に一様に分布しているわけではありません。最大応力は梁の最外層、つまり中立軸から最も遠い層で発生します。中立軸とは、曲げ応力がゼロになる梁の長さに沿った線です。

曲げ応力を理解することは、構造物の全体的な強度と寿命を決定する上で重要な役割を果たします。過剰な曲げ応力は、構造物の変形、破壊、さらには崩壊につながる可能性があります。そのため、設計者やエンジニアにとって、構造物の破壊を予測し防止するためには、曲げ応力と法線応力の理論的基礎を理解することが不可欠です。

さまざまな材料がさまざまな種類の応力にどのように反応するかを含む材料力学を学ぶことは、曲げ応力を理解するための重要な基礎となります。この知識は、曲げ応力に効果的に耐える適切な材料と設計の選択に役立ち、構造の安全性と信頼性を確保します。

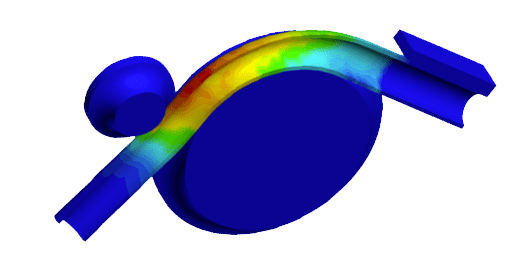
図1: 応力分布を示すパイプの曲げシミュレーション結果

曲げ応力の計算方法: 重要な公式

曲げ応力の計算は、加えられるモーメント、中立軸から対象点までの距離、断面積の慣性モーメントを包含する基本的な曲げ応力公式に基づいています。曲げ応力 ($\sigma$) の標準的な計算式¹は

$$ \sigma = M \frac{\gamma}{I} $$

です。ここで、$M$ は部品にかかるモーメントまたは曲げ力、$\gamma$ は中立軸から応力を計算する必要がある点までの距離、$I$ は中立軸に対する断面積の慣性モーメントです。

慣性モーメントは断面の形状によって計算方法が異なります。慣性モーメントは、特定の形状がもたらす曲げに対する抵抗力を示します。長方形の断面の場合、慣性モーメント($I$)²は

$$ I = \frac{b \cdot h^3}{12} $$

です。ここで、$b$ は長方形断面の幅、$h$ は長方形断面の高さです。。

中立軸から断面の上端または下端までの「$\gamma$」の値を調整することで、梁の断面全体における曲げ応力の変化を把握することができます。これらは最大曲げ応力が発生する場所です。

曲げ応力を正確に計算することは、構造解析に不可欠です。これは、選択した材料と設計が、降伏や破壊を起こさずに課された荷重に耐えられるかどうかを判断するのに役立ちます。

計算された曲げ応力が材料の許容応力を超える場合、検討中のコンポーネントの構造上の安全性と信頼性を確保するために、設計の変更や材料の代替が必要になることがあります。

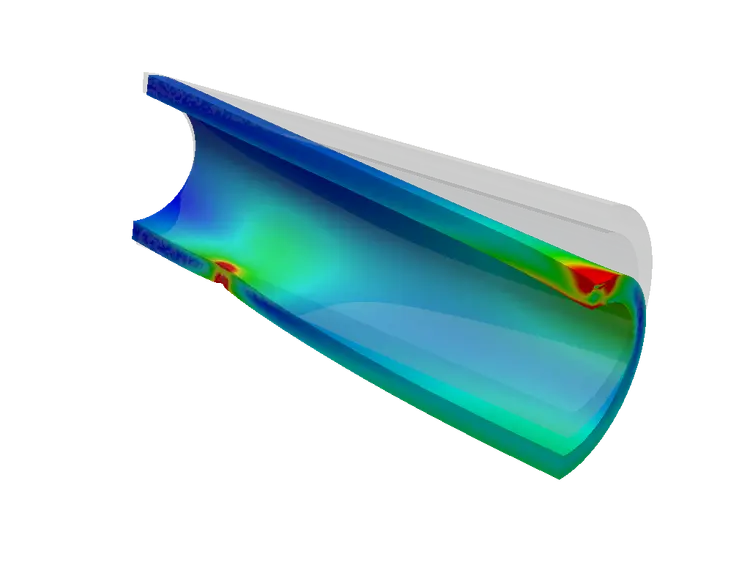
図2: 応力と曲げ角度

梁曲げの科学

材料力学の基本原理は、フックの法則を一般化した現代の弾性理論によって定義される応力とひずみの関係です。これはフックの法則を一般化したもので、材料が降伏強度に達していなければ、材料に加わる応力はひずみに正比例するというものです。数学的には、この関係は次の式で表されます^[2]

$$ \sigma = E \cdot \epsilon $$

ここで、$\sigma$ は応力、$E$ は弾性率(またはヤング率)、$\epsilon$ はひずみです。

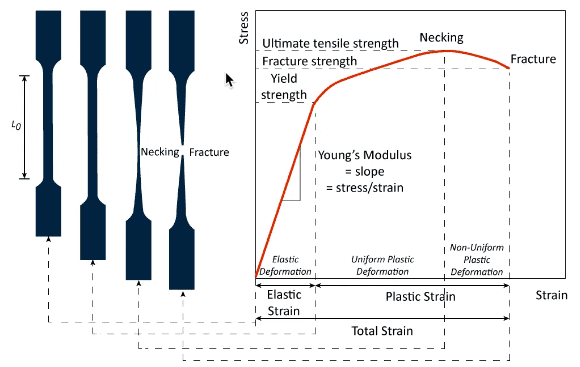
これは応力-ひずみ曲線でさらに可視化することができ、材料が負荷の下でどのように挙動するかを示し、材料の強度、剛性、延性、および破壊限界についての洞察を与えます。材料が応力を受けると、ひずみが生じ、形状が変化する可能性があります。この挙動は応力-ひずみ曲線でグラフ化することができます。この曲線は通常、フックの法則が適用される直線領域から始まります。弾性限界(降伏強さとも呼ばれる)を超えると、材料は塑性変形し、応力が増加し続けると最終的に破壊する可能性があります。

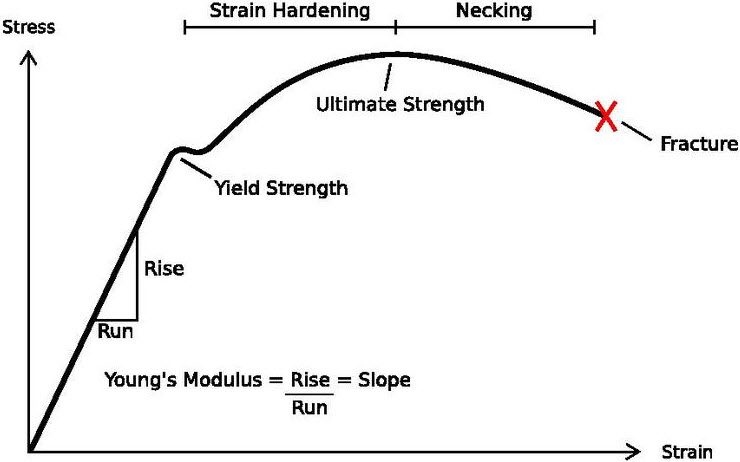
図3: 延性材料の応力-ひずみ曲線

梁の曲げは、曲げ応力解析の最も一般的な例の 1 つです。梁は、長さ方向に一定の断面を持つ一般的な物体です。長さは断面の寸法よりもかなり大きいため、比較的正確な近似が可能です。その単純さから、梁は他の構造物の近似に適しており、1 つの梁または梁のグループと見なすことができます。

梁を曲げると、他の構造物と同様に、材料の降伏強度と応力の大きさに応じて、弾性的または塑性的に機械的に変形します。梁の応力解析の例を示します。SimScaleのFEA静解析(次のセクションで説明)を使用して、設計者はフランジの曲げ応力、軸方向引張、圧縮を解析しました。

図4: 梁の応力解析

シミュレーション解析: FEAによる曲げ応力の解析

シミュレーション解析は、エンジニアが構造解析に取り組む方法に革命をもたらしました。曲げ応力を含むさまざまな応力に対する構造物の応答を正確に予測し、解析するためのプラットフォームを提供します。この強力なツールにより、エンジニアや設計者は、さまざまな荷重条件下での設計性能を予測し、製造前に最適化することができます。

有限要素解析(FEA)は、このような場面で威力を発揮します。FEAは、与えられた条件下で部品やアセンブリがどのように動作するかを予測するために使用される数値手法です。FEAでは、四面体や立方体のような単純で小さな「有限要素」を多数組み合わせたメッシュを作成します。これらの要素は「節点」で相互に接続され、メッシュ全体を使用して元の構造に近い近似を作成することができます。荷重下での各有限要素の挙動は、曲げケースの曲げ応力公式などの関連方程式を使用して計算され、これらの結果は、指定された荷重条件下で構造がどのように反応するかの全体像を提供するために集約されます。

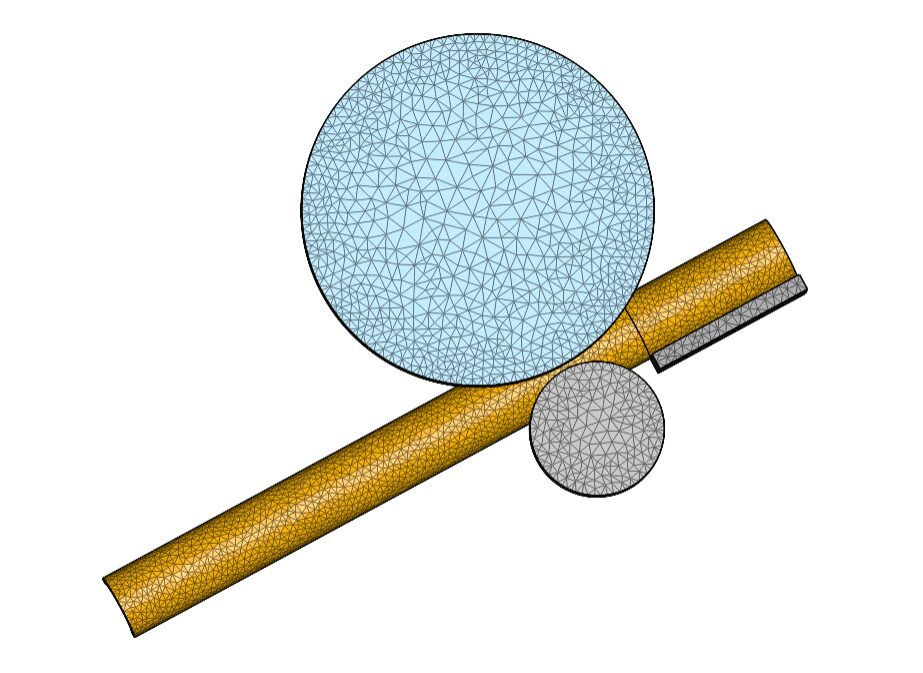
図5: メッシュ可視化の例

FEA を使用することで、エンジニアは設計内の曲げ応力(およびその他の種類の応力)の高い領域を視覚化し、潜在的な弱点や破損箇所を特定することができます。設計段階でこのような解析を行うことで、曲げ応力に対する構造物の耐性を向上させる設計変更を実施することができ、材料の無駄やコストを削減しながら安全性と効率を高めることができます。

さらに、シミュレーション解析では、極端な荷重条件や長期間の使用による影響など、物理的に試験することが現実的でないさまざまな要因を考慮することができます。また、構造物の性能を最適化するために、異なる設計構成、材料、または荷重条件間の比較検討も可能です。

曲げ応力解析では、シミュレーションによって理論的な知識を実践的な洞察で補完することで、より深い理解が得られます。これにより、より安全で効率的な構造物の作成が容易になり、設計の最適化や意思決定プロセスの支援が可能になります。このため、シミュレーション解析は今日のエンジニアや設計者にとって不可欠なツールであり、曲げ応力解析の現代的なアプローチに不可欠なものとしてその価値が強調されています。

結論: 曲げ応力シミュレーションの重要性

曲げ応力を理解することは、材料の力学を掘り下げ、特定の公式を適用することを含み、安全性と効率性の両方において構造解析に不可欠です。技術の進歩に伴い、シミュレーション解析は、エンジニアに予測的な洞察を提供し、物理的に実現する前に設計を改善することを可能にする、不可欠なツールとして台頭してきました。

構造工学では、理論的理解とシミュレーション解析の両方を通じて曲げ応力を習得することが基礎となります。要するに、曲げ応力を理解することで、設計者やエンジニアは、構造物が荷重に耐えられるかどうかだけでなく、耐えられるかどうかも判断できるようになります。この理解とSimScaleのようなシミュレーションツールの活用により、より安全で効率的な設計が可能になります。

図6: アルミパイプのフォンミーゼス応力発生を示す曲げプロセス

参考

Beer, F. P., Johnston, E. R., DeWolf, J. T., & Mazurek, D. F. (2020). Mechanics of Materials (8th ed.). New York: McGraw-Hill.
Hibbeler, R. C. (2022). Mechanics of Materials (11th ed.). Pearson.

2024年3月13日