有限要素解析(Finite Element Analysis | FEA)とは、有限要素法(Finite Element Method | FEM)と呼ばれる数値解析技術を用いて、任意の物理現象をシミュレーションすることです。エンジニアはFEAソフトウェアを使用して、物理的な試作品や実験の回数を減らし、設計段階でコンポーネントを最適化することで、費用を節約しながらより良い製品をより早く開発することができます。
構造物や流体の挙動、熱輸送、波動伝播、生物細胞の成長など、あらゆる物理現象を包括的に理解し定量化するためには、数学を使用する必要があります。これらのプロセスのほとんどは偏微分方程式(PDE)を用いて記述されます。コンピュータがこれらの偏微分方程式を解くために、ここ数十年の間に数値計算技術が開発されてきました。
微分方程式は自然現象だけでなく、工学力学で遭遇する物理現象も記述します。これらの偏微分方程式は複雑な方程式であり、構造物の関連量(応力(\(\epsilon\))、ひずみ(\(\epsilon\))など)を計算し、与えられた荷重下での構造物の挙動を推定するために解く必要があります。FEAは問題の近似解を与えるだけであり、偏微分方程式の実際の結果を得るための数値的アプローチであることを知っておくことが重要です。
簡単に言えば、FEAは、部品やアセンブリが与えられた条件下でどのように振る舞うかを予測するために使用される数値手法です。
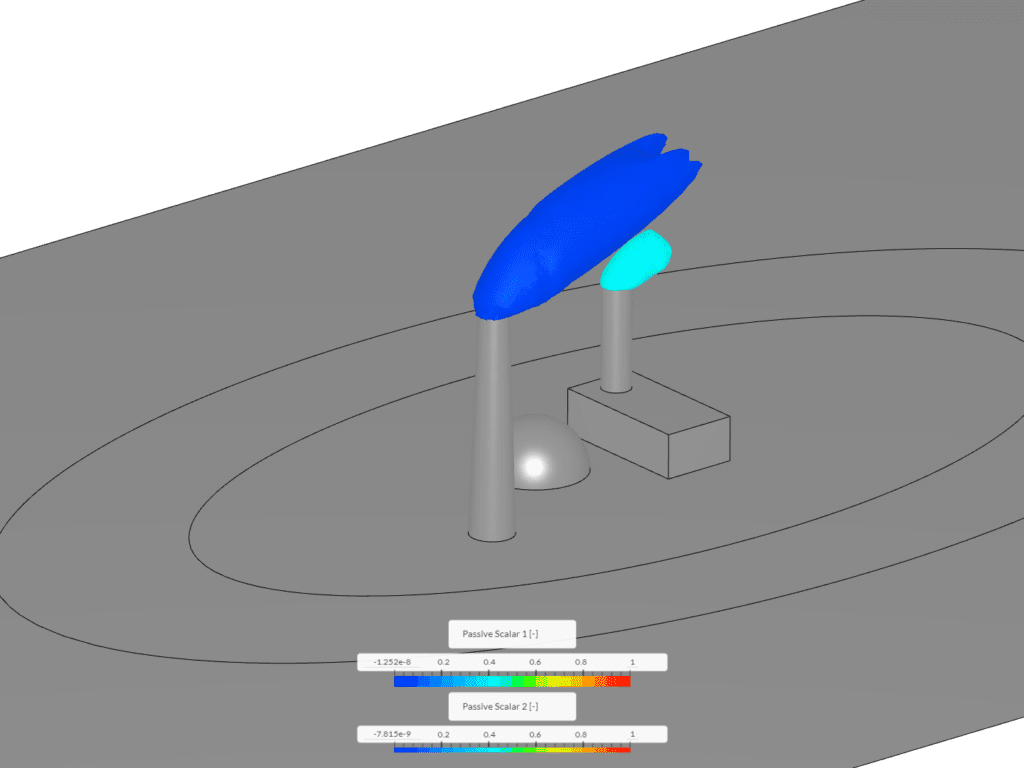
FEAは最新のシミュレーション・ソフトウェアの基礎として使用され、エンジニアが設計の弱点や張力のかかる部分などを見つけるのに役立ちます。FEAに基づくシミュレーションの結果は、通常、例えば対象物上の圧力分布を示すカラースケールで表示されます。
見方によっては、FEAの起源は16世紀のオイラーの研究にあると言えます。しかし、有限要素解析に関する最古の数学論文は、Schellbach [1851]とCourant [1943]の著作に見ることができます。
FEAは、航空宇宙や土木工学に関連する構造力学の問題に対処するために、さまざまな業界のエンジニアによって独自に開発されました。Turner, Clough, Martin & Topp [1956]、Argyris [1957]、Babuska & Aziz [1972]の論文に見られるように、実生活への応用を目指した FEA の開発は 1950 年代半ばに始まりました。また、Zienkiewicz [1971]やStrang & Fix [1973]の書籍は、将来のFEAソフトウェア開発の基礎を築きました。
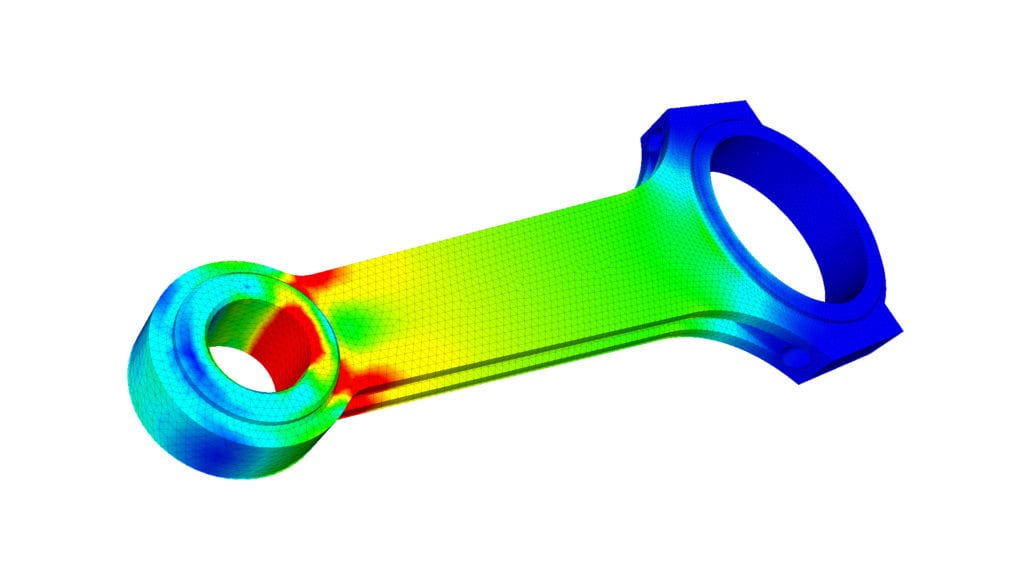
図 1: ピストンロッドの FEA シミュレーション
FEA の近似
シミュレーションを行うには、構造物の形状を形成する最大数百万個の小さな要素からなるメッシュを作成する必要があります。計算はすべての要素に対して行われます。個々の結果を組み合わせることで、最終的な構造結果が得られます。
今述べた近似は通常多項式であり、実際には要素上で補間されます。つまり、要素内の特定の点での値はわかりますが、すべての点での値はわかりません。この「特定の点」は節点と呼ばれ、多くの場合要素の境界に位置しています。変数が変化する精度は、1次、2次、3次などの近似で表されます。
近似技術の理解を深めるために、一次元の棒を見てみましょう。下の図の棒に沿った真の温度分布T(x)を考えます:
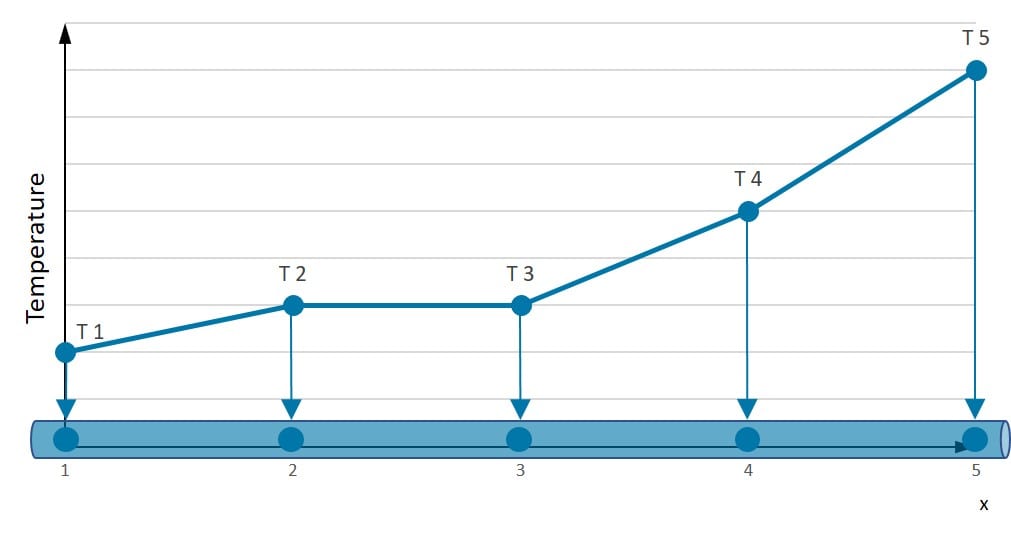
図2: 結節値間を線形近似した棒の長さに沿った温度分布。
この棒の温度が5つの特定の位置(図の番号1-5)でわかっているとします。これらの点間の温度を予測するにはどうすればよいでしょうか?線形近似は非常に良いですが、実際の温度分布を表すにはもっと良い可能性があります。
正方形近似を選ぶと、棒に沿った温度分布はより滑らかになります。とはいえ、多項式の次数に関係なく、節点での値がわかれば棒に沿った分布はわかることがわかります。
もし無限の棒があれば、無限の未知数(自由度(Degree of Freedom | DOF))を持つことになります。しかし、この場合の未知数の数は「有限」です。
有限個の未知数を持つシステムは離散システムと呼ばれます。
無限個の未知数を持つシステムは連続システムと呼ばれます。
近似の目的で、ある場の量\(u(x)\) について次の関係を求めることができます:
$$ u(x) = u^h(x) + e(x) \tag{1}$$
ここで、\(u^h(x)\) は近似値で、実解\(u(x)\) とは異なります。\(e(x)\) は誤差項です。事実上、この誤差項は、近似解\(u^h(x)\) が有効になるように消滅しなければなりません。ここで生じる疑問は、\(u^h(x)\) を離散関数空間でどのようにパラメータ化できるかということです。一つの可能な解は、\(u^h(x)\) を、係数\(\alpha_i(x)\) を持つ形状関数\(\phi_i(x)\) の和として表現することです。
$$ u^h(x) = \sum_{i=1}^n \alpha_i\phi_i(x) \tag{2}$$
\(u\) は、不均一に加熱された棒の長さに沿った温度を表すことができます。この場合、x軸に沿って4つの要素があり、関数は線に沿って点で示された温度の線形近似を定義します。
有限要素解析を使用する最大の利点の1つは、要素ごとに離散化を変えるか、対応する基底関数を離散化できることです。事実、\(u\) の高い勾配が予想される領域では、より小さな要素を使用することができます。関数の急勾配をモデル化するためには、近似を行う必要があります。
偏微分方程式 (PDE)
FEAそのものを進める前に、PDEの種類とFEAへの適合性を理解することが重要です。このことを理解することは、有限要素解析を使用する動機に関係なく、誰にとっても重要です。
FEA ソフトウェアは道具であり、道具は使い手次第であることを常に心に留めておく必要があります。
PDEは次のように分類できます:
- 楕円型:非常に滑らか
- 双曲型:不連続な解をサポートします。
- 放物型:時間依存の拡散問題を記述します。
これらの微分方程式を解く際には、境界条件や初期条件を与える必要があります。PDEのタイプに基づいて、必要な入力を評価することができます。各偏微分方程式の例としては、ポアソン方程式(楕円型)、波動方程式(双曲型)、フーリエ則(放物型)などがあります。
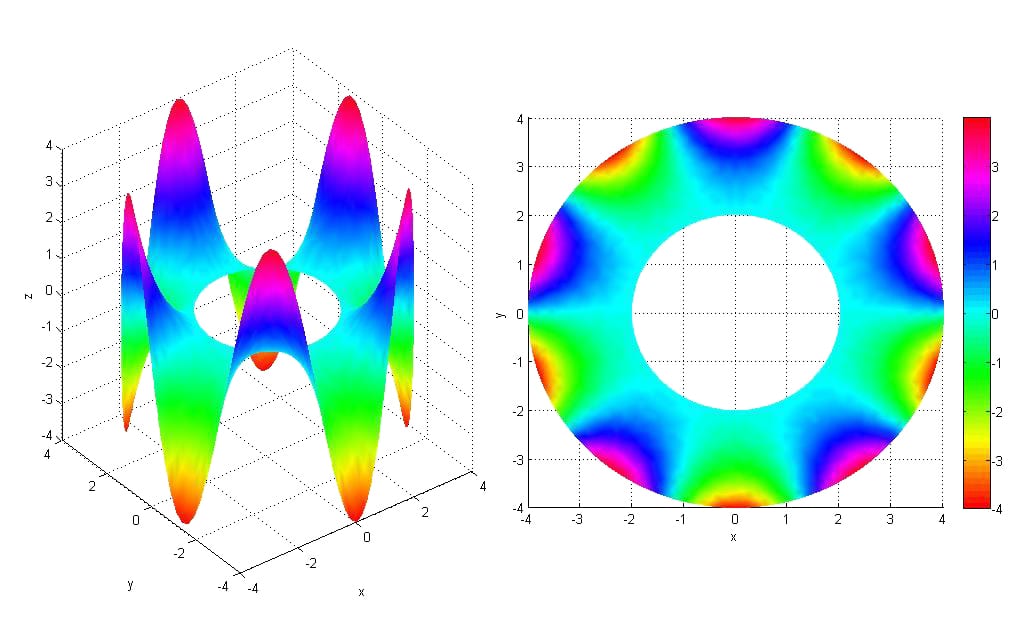
図3: 環状体上のラプラス方程式解析;等角図(左)と上面図(右)
楕円型偏微分方程式を解くには、有限差分解析と変分法(またはエネルギー法)の2つの主なアプローチがあります。FEAは2番目の変分法に分類されます。変分法は主にエネルギー最小化の哲学に基づいています。
双曲型偏微分方程式は一般的に解の不連続性を伴います。例えば、波動方程式は双曲偏微分方程式です。解に不連続性が存在するため、元のFEA技術(またはブブノフ・ガラーキン法)は双曲型偏微分方程式を解くのに適していないと考えられていました。しかし、長年にわたり、FEAソフトウェアと技術の適用範囲を拡大するための改良が開発されてきました。
選択された偏微分方程式のタイプに適さない数値的フレームワークを使用した場合の結果を考慮することが重要です。このような使い方は、不適切な解につながります。これは、領域パラメータの小さな変化が解の大きな振動につながったり、解が領域や時間の特定の部分にしか存在しなかったりすることを意味します。これらの結果は信頼できません。
精度よく解かれた解は、定義されたデータに対して連続的に存在する一意解で定義されます。したがって、信頼性を考慮すると、解を求めることは非常に重要です。
弱定式化と強定式化
熱伝導と弾塑性の数学モデルは、初期条件と境界条件を持つ偏微分方程式で構成されています。これはいわゆる問題の「強形式」とも呼ばれます。「強形式」の例をいくつか下表に示します。
微分方程式 |
物理的問題 |
量 |
| \(\frac{d}{dx}\left(Ak\frac{dT}{dx}\right)+Q=0\) | 一次元熱流 | \(T\) = 温度, \(A\) = 面積, \(k\)= 熱伝導率, \(q\)= 供給熱量 |
| \(\frac{d}{dx}\left(AE\frac{du}{dx}\right)+b=0\) | 軸方向に荷重をかけた弾性棒 | \(u\) = 変位、 \(A\) = 面積、 \(E\) = ヤング率、 \(b\) = 軸方向荷重 |
| \(S\frac{d{^2}w}{dx{^2}}+p=0\) | 横荷重可撓弦 | \(w\) = たわみ、 \(S\) = 張力、 \(p\) = 横荷重 |
| \(\frac{d}{dx}\left(AD\frac{dc}{dx}\right)+Q=0\) | 一次元拡散 | \(c\) = イオン収縮、 \(A\) = 面積、 \(D\) = 拡散係数、 \(Q\) = イオン供給量 |
| \(\frac{d}{dx}\left(A\gamma\frac{dV}{dx}\right)+Q=0\) | 一次元電流 | \(V\) = 電圧、 \(A\) = 面積、 \(\gamma\) = 電気伝導率、 \(Q\) = 電荷供給。 |
| \(\frac{d}{dx}\left(A\frac{D{^2}}{32\mu}\frac{dp}{dx}\right)+Q=0\) | パイプ内の層流(ポアズイユ流) | \(p\) = 圧力、 \(A\) = 面積、 \(D\) = 直径、 \(mu\) = 粘性、 \(Q\) = 流体供給。 |
二階偏微分方程式は、解\(u(x)\) に対して高度な平滑性を要求します。つまり、変位の2階微分が存在し、連続でなければなりません。これはまた、形状(鋭いエッジ)や材料パラメータ(材料の異なる弾性率)に影響を受けることを意味します。
有限要素定式化を開発するためには、偏微分方程式を弱形式と呼ばれる積分形式で記述し直す必要があります。弱形式と強形式は等価です。応力解析では、弱形式を仮想仕事の原理と呼びます。
$$ \int^l_0\frac{dw}{dx}AE\frac{du}{dx}dx=(wA\overline{t})_{x=0} + \int^l _0wbdx ~~~ \forall w~with ~w(l)=0 \tag{3}$$
与えられた方程式はいわゆる弱形式(この場合、弾性体の弱形式)です。弱形式の解は強形式の解ほど滑らかである必要はなく、連続性の要件が弱いことを意味します。
弱形式を満たす解は、強形式の方程式の解でもあることを覚えておいてください。また、試行解(\(u(x)\) )は変位境界条件を満たさなければならないことも覚えておいてください。これは試行解の本質的な性質であり、境界条件を本質的境界条件と呼ぶのはこのためです。
最小ポテンシャルエネルギー変分原理
有限要素解析は変分原理でも実行できます。一次元弾塑性力学の場合、最小ポテンシャルエネルギーは保存系に対して弾力的です。システムのポテンシャルエネルギー(\(\Pi\) )が最小であれば、平衡位置は安定です。安定位置の無限小の擾乱は、エネルギー的に不利な状態をもたらし、復元反応を意味します。
簡単な例は、ポテンシャルエネルギーが最小となる地面に立っている普通のガラス瓶です。倒れても、大きな音がするだけで、何も起こりません。テーブルの角の上に立っていて地面に倒れれば、地面に向かうエネルギーが大きくなるので、むしろ壊れる可能性が高くなります。変動原理では、この事実を利用します。エネルギー準位が低ければ低いほど、間違った解を得る可能性は低くなります。システムの全潜在エネルギー\(\Pi\) は、内力(ひずみエネルギー)の仕事から構成されます。
$$ A_i = \int_0^l \underbrace{\frac{1}{2} E(x)A(x) \left(\frac{du}{dx} \right)^2}_{\frac{1}{2}\sigma\epsilon A(x)} dx \tag{4}$$
と外力の仕事
$$ A_a = A(x)\overline{t}(x)u(x)|_{\Gamma _t} \tag{5}$$
合計エネルギーは
$$ \Pi = A_i – A_a \tag{6}$$
メッシュの収束
計算力学において、精度に影響する最も見過ごされがちな問題の1つがメッシュの収束です。これは、メッシュサイズを変更しても解析結果が影響を受けないようにするために、要素をどの程度小さくする必要があるかに関連しています。
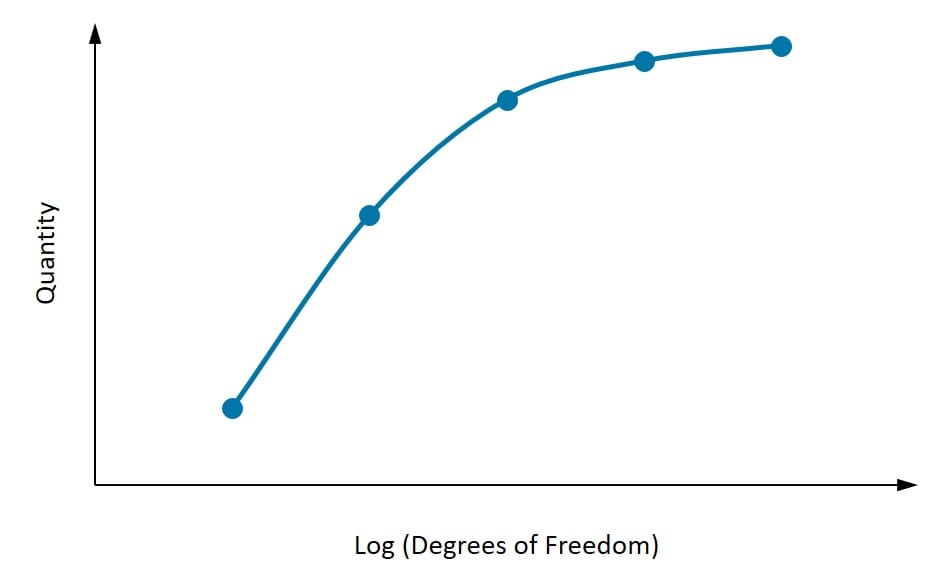
図4: 自由度(DOF)の増加に伴う量の収束。DOFの増加に伴って収束する様子が見えます。
上の図は、自由度の増加に伴う量の収束を示しています。図に描かれているように、まず関心のある量を特定することが重要です。少なくとも3つの点を考慮する必要があり、メッシュ密度が高くなるにつれて、関心量は特定の値に収束し始めます。その後2回メッシュを微細化しても結果が大きく変わらない場合は、収束したと考えることができます。
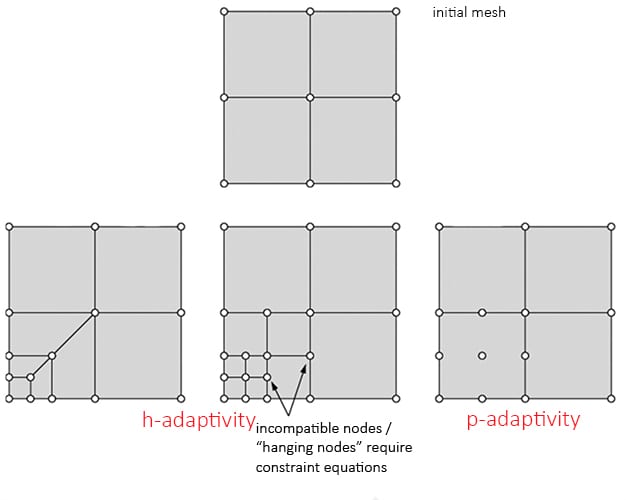
図5: h型とp型を使ったメッシュ精密化は収束をはやくできます
メッシュのリファインメントについては、必ずしもモデル全体のメッシュをリファインメントする必要はありません。St.Venantの原理は、ある領域の局所応力が他の領域の応力に影響しないことを強制します。したがって、物理的な観点からは、特定の関心領域でのみモデルを微細化し、さらに粗いメッシュから細かいメッシュへの移行領域を設けることができます。
上の図5に示すように、精密化には2つのタイプ(h-refinementとp-refinement)があります。h-refinementは要素サイズの縮小に関するもので、p-refinementは要素の次数の増加に関するものです。
ここで、特に曲面をメッシュ化する場合、幾何学的効果とメッシュ収束を区別することが重要です。直線(または線形)要素を使用すると、境界を正確に捉えるために、より多くの要素(またはメッシュの微細化)が必要になります。メッシュの精密化は誤差の大幅な減少につながります。
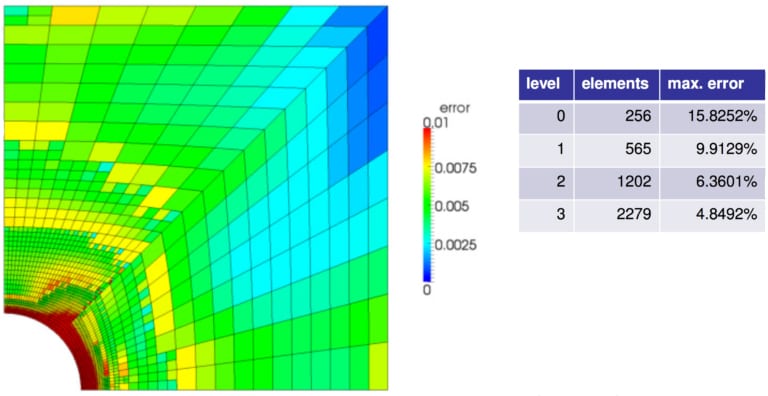
図6: メッシュ精密化の実用的なアプリケーション。大きな変動勾配とともに複雑な幾何学的特徴を捉えるには、高密度の要素が必要です。
このような精緻化により、解かれる問題全体のサイズを大きくすることなく、解の収束性を高めることができます。
収束の測定方法
さて、収束の重要性について述べてきましたが、収束はどのように測定できるのでしょうか?収束の定量的な尺度とは何でしょうか?第一の方法は、解析解や実験結果と比較することでしょう。
変位の誤差:$$ e_u = u – u^h \tag{7}$$
\(u\) は変位場の解析解。
ひずみの誤差:$$ e_\epsilon = \epsilon – \epsilon^h \tag{8}$$
\(\epsilon\) はひずみ場の解析解。
応力の誤差:$$ e_\sigma = \sigma – \sigma^h \tag{9}$$
\(\sigma\) は応力場の解析解。
上式で示したように、変位、ひずみ、応力に対していくつかの誤差を定義することができます。これらの誤差は比較に使用することができ、メッシュの細分化によって減少させる必要があります。
有限要素解析ソフトウェア

図7: FEAの適用例 - 車軸。応力やひずみのような敏感な量を把握するために、重要な部分のメッシュが改良されているのがわかります。
有限要素解析は、航空宇宙および土木工学に関連するいくつかの機械的アプリケーションのモデリングにおいて、大きな可能性を持って始まりました。有限要素法の応用は、その潜在能力を発揮し始めたばかりです。
最も待ち望まれている展望の1つは、流体と構造の相互作用のような連成問題、熱機械、熱化学、熱化学機械問題、圧電、強誘電、電磁気、およびその他の関連分野への応用です。
有限要素法(FEM)の種類
偏微分方程式の章で前述したように、従来の FEM 技術は、流体力学や波動伝播などに関する問題のモデリングに欠点がありました。過去20年の間にいくつかの改良が加えられ、解法プロセスが改善され、有限要素解析の適用範囲が幅広いジャンルの問題に拡大されました。現在も使用されている重要なものには、次のようなものがあります:
拡張有限要素法 (XFEM)
ブブノフ・ガラーキン法は、要素間の変位の連続性を必要とします。しかし、接触、破壊、損傷などの問題は、有限要素法では直接扱えない不連続性やジャンプを伴います。この欠点を克服するために、1990年代にXFEMが誕生しました。
XFEMは、形状関数をHeavisideステップ関数で展開します。ジャンプを考慮できるように、不連続点周辺の節点に余分な自由度を割り当てます。
一般化有限要素法(GFEM)
GFEMは、90年代のXFEMと同時期に導入されました。従来のFEMソフトウェアとメッシュレス法の特徴を兼ね備えています。形状関数は主にグローバル座標で定義され、ローカル要素の形状関数を作成します。GFEMの利点の1つは、特異点周辺での再メッシュを防止できることです。
混合有限要素法
接触や非圧縮性のようないくつかの問題では、ラグランジュ乗数を使用して制約が課されます。ラグランジュ乗数から生じるこれらの余分な自由度は独立して解かれます。方程式は連立方程式のように解かれます。
hp有限要素法 (hp-FEM)
hp-FEMは自動メッシュ細分化(h-refinement)と多項式次数の増加(p-refinement)を組み合わせたものです。これはh-refinementとp-refinementを別々に行うのとは異なります。自動的なhp-refinementが使用され、要素がより小さな要素に分割される場合、各要素は同様に異なる多項式次数を持つことができます。
不連続ガラーキン有限要素法(DG-FEM)
DG-FEMは、従来の有限要素法では困難であった双曲線方程式の解法に、有限要素の考え方を用いることで大きな可能性を示しました。さらに、ほとんどの材料プロセスで一般的に見られる曲げや非圧縮性の問題でも有望視されています。ここでは、(相互貫入を防ぐための)ペナルティパラメータや、要素間の応力の他の平衡のための項など、弱形式に追加の制約が加えられています。
参考
- Jacob Fish and Ted Belytschko, “A First Course in Finite Elements by Jacob Fish and Ted Belytschko”, Wiley, 2007
- R . Courant, “Variational methods for the solution of problems of equilibrium and vibrations”, 1943
- K . Schellbach, “Probleme der Variationsrechnung”, 1851, Berlin
SimScale製品紹介資料ダウンロード

資料請求
資料全体をご希望の方はこちらのフォームからお申し込みください。