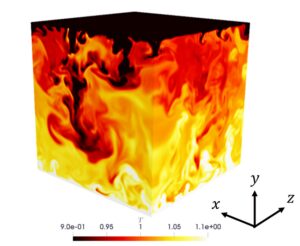
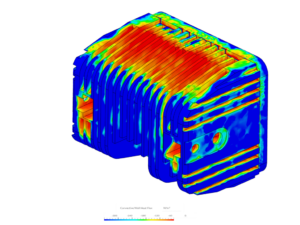
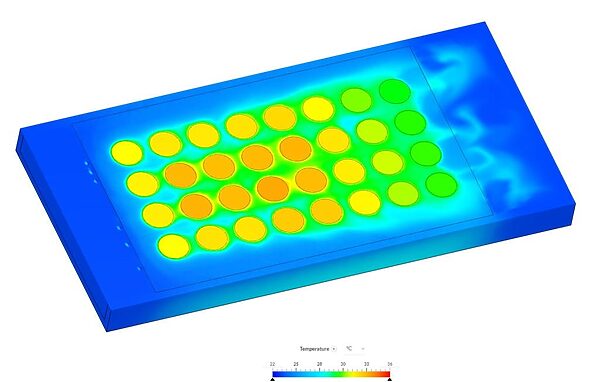
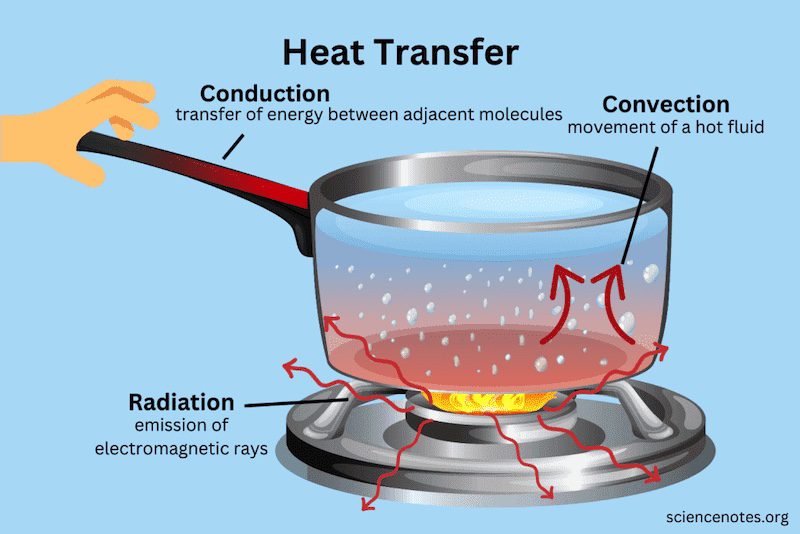
伝導とは、熱エネルギーがある場所から別の場所に伝達される3つの主な方法の1つです。伝導は、主に固体や液体の物質において、隣り合う原子や分子の衝突によって起こります。伝導は粒子が密に詰まっている物質ではより重要です。
互いに接触している物質間の温度差が大きいと、伝導の影響は大きくなります。伝導の典型的な例は、お湯を入れた鍋の取っ手が数分後に温かくなるのに気づく場合です。熱を伝えるために直接物理的な接触を伴うものはすべて、伝導の例です。
フーリエの熱伝導の法則
偏微分方程式で記述される熱伝導の過渡過程は、ジャン・バティスト・ジョセフ・フーリエ(1768-1830)によって初めて定式化され、1807年にフランス学士院に原稿として提出されました。しかし、原稿を発表してから15年後、フーリエは1822年に著書 "Théorie Analytique de la Chaleur "で熱伝導に関する完全な理論を定式化しました。
フーリエの法則は、熱流束は温度勾配の大きさに正比例するというものです。
$$q=-k\frac{\Delta T}{\Delta x}$$
ここで
- k: 材料の熱伝導率
- \(\frac{\Delta T}{\Delta x}\): 温度勾配

熱流束はベクトル量であり、温度が下がるとqは正のx方向に流れます。言い換えれば、熱は高温から低温に流れます。x、y、zの3次元の式は下記の通りです。
$$\bar q=-k \nabla T$$
ここで、\(\nabla\) は勾配を示します。
熱伝達率
熱伝達率とは、ある物質において単位時間当たりに移動する熱量のことで、通常はワット(ジュール毎秒)で表されます。フーリエの熱伝導の法則に基づくと、熱伝達の速度は次のようになります:
$$\frac{Q}{\Delta t}=-kA\frac{\Delta T}{\Delta x}$$
ここで
- \(Q\): 正味熱伝導量(W)
- \(\Delta t\): 所要時間(秒)
- \(\Delta T\): 温度差(K)
- \(\Delta x\): 熱を伝える材料の厚さ(m)
- \(k\): 熱伝導率(単位: W/(m.K))
- \(A\): 熱を放出する面の表面積(m2)
熱伝導率に影響を与える要因
伝導の問題を考えるとき、熱伝導の発生速度に影響するパラメー タは以下の通りです:
- 幾何学的特性
- 材料の断面積
- 材料の厚さ
- 温度差
- 熱伝導率(材料特性)
幾何学的特性
伝導は、断面積Aや材料の厚さ\(\Delta x\) などの幾何学的特性に依存します。
$$\dot Q \propto A$$
$$\dot Q \propto \frac{1}{\Delta x}$$
断面積が大きいほど、分子間の衝突が多くなるため、熱伝導は速くなります。一方、材料の厚さは熱伝導率に反比例します。
温度差
伝導は、材料の異なる部分内または接触している2つの材料間に温度差がある場合にのみ起こります。さらに、温度差が大きいほど、単位時間当たりの熱伝導率は高くなります。
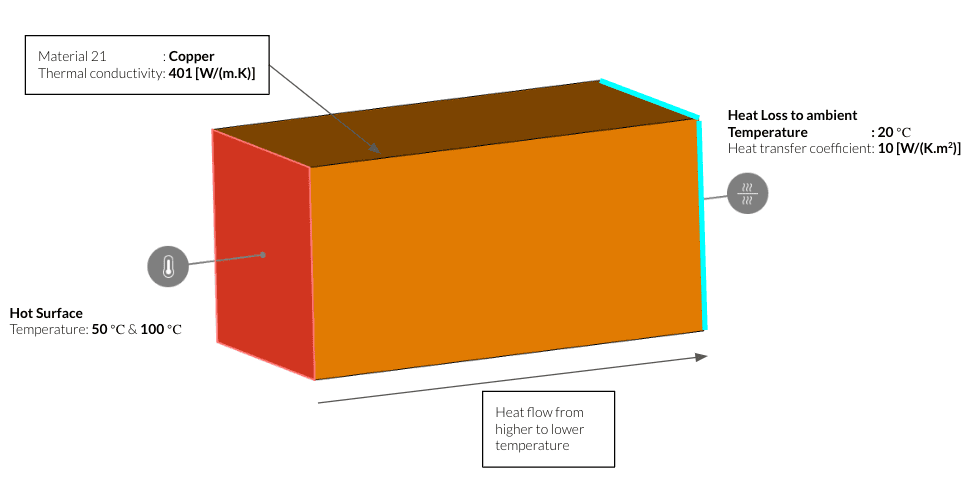
この挙動を理解するために、SimScaleの熱伝導解析を使って2つの異なる温度勾配を簡単にシミュレーションすることができます。高温側と低温側を持つ固体材料を考えてみましょう。
| ケース | 高温側 |
低温側 |
| 1 | 50° C | 20℃、熱損失10W/K. m 2 |
| 2 | 100° C | 20° C、熱損失10 W/K. m2 |
シミュレーションが終了し、SimScaleの比較フィルターを使用すると、以下のケースの質的な違いがはっきりとわかります:
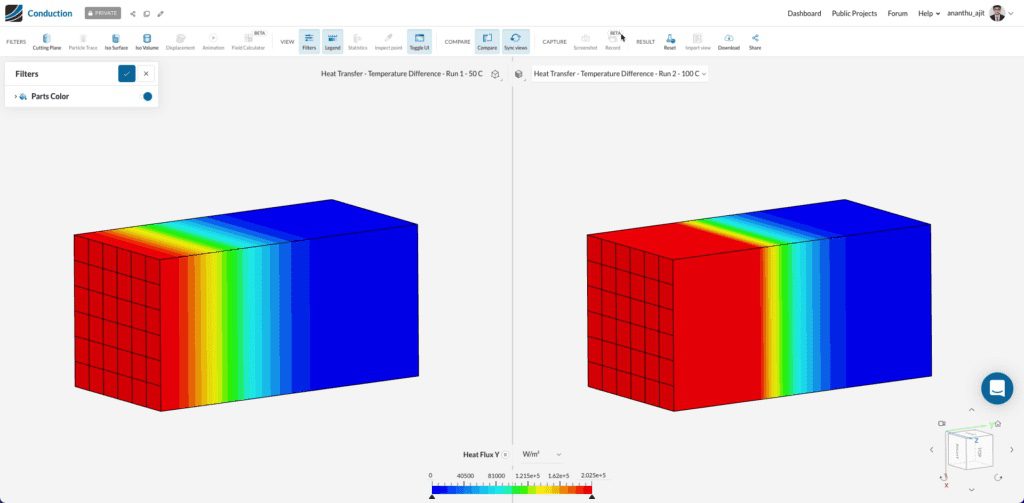
正確な材料特性と10秒間の過渡シミュレーションを行った場合、温度差が大きいため、2番目のケースを通過する熱流束は1番目のケースを通過する熱流束よりもはるかに高くなっています。これは、高温表面の熱流結果モニターを使用して定量的に見ることができます。
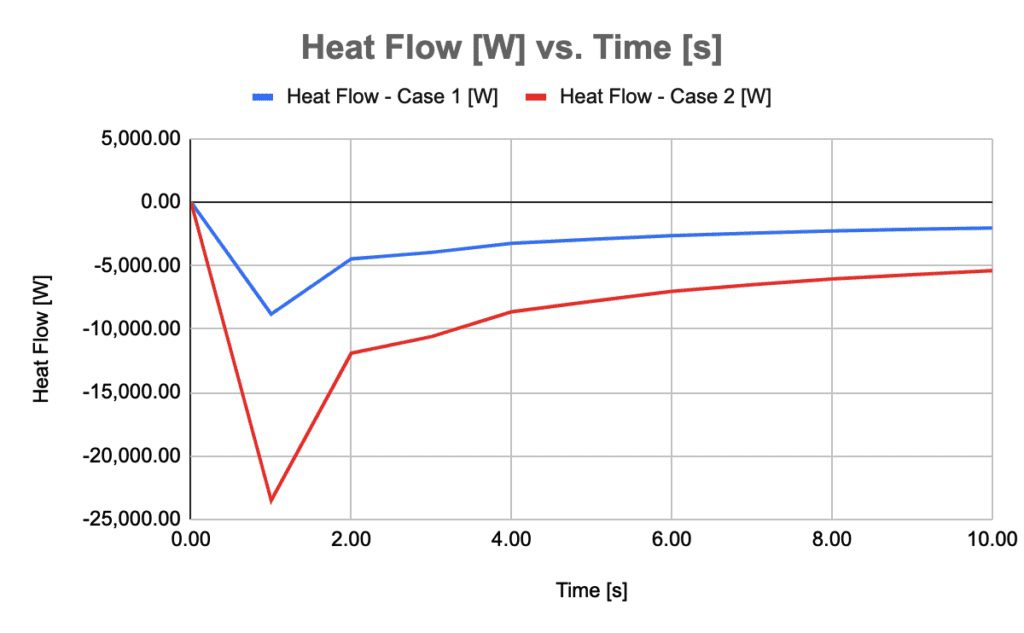
10秒の運転時間で比較すると、温度差の大きいケース(100℃)の方が高い熱流量を示しています。
注: 熱流の負の値は、フーリエの熱伝導の法則に従った高温面からの熱損失を表しています。
熱伝導率
材料の熱伝導率は、熱を伝導する能力を数値化したものです。各材料は、その中の電子の配列に基づいて独自の熱伝導率を持っています。金属など、熱を伝えやすい材料もあります。
原理的には、自由電子が存在すると分子間の衝突が速くなり、熱伝導率が向上します。熱伝導率が高い材料は熱伝導体として、熱伝導率が低い材料は絶縁体として振る舞います。
気体の場合、分子の相互作用が熱伝導率を決定します。物質内の分子は、下の図に示すように、ある位置から別の位置へと移動します:
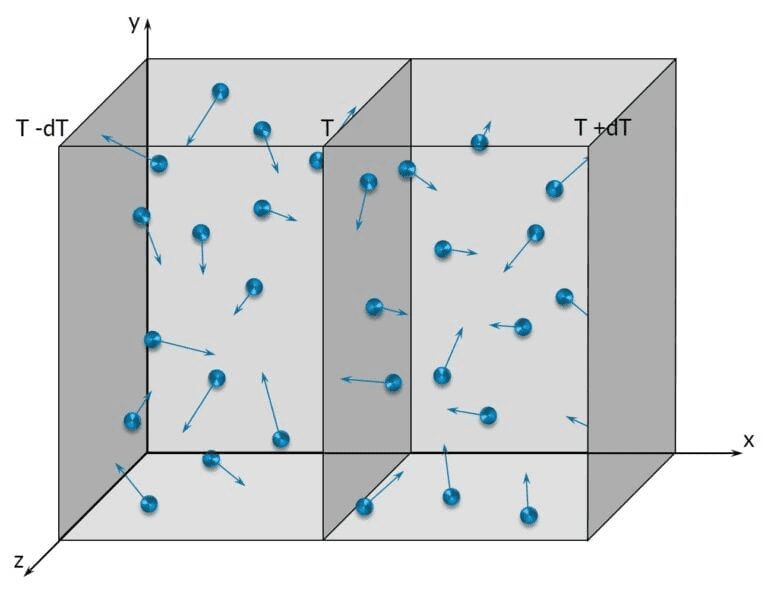
分子の内部エネルギーは他の分子との衝突によって移動します。その結果、温度の低い領域は温度の高い分子に占有され、逆もまた然りです。熱伝導率はこのモデルで説明でき、気体の運動論から導かれます[4]:
$$T=\frac{2}{3} \frac{K}{N\left(k_B\right)}$$
ここで
- \(K\): 分子の運動エネルギー
- \(N\):モル数
- \(K_{B}\): ボルツマン定数
- \(T\): 絶対温度
この式は、「理想気体の場合、平均分子運動エネルギーは絶対温度に正比例する」と述べています[6]。熱伝導率は圧力に依存せず、温度の根に比例して増加することに注意することが重要です。
一般に、気体以外の物体について運動論を理解するのはかなり困難です。流体の場合は、単純な理論がないため、さらに難しくなります。非金属部品では、熱伝導は格子振動(フォノン)を介して起こりますが、これはこの記事の範囲外です。
下の表は、いくつかの一般的な材料の熱伝導率を示しています [5]:
材料 |
熱伝導率 K \(\frac{W}{\text {m.K}}\) |
| 銀 | 429 |
| 銅 | 401 |
| アルミニウム | 235 |
| 鋼 | 60 |
| 鋳鉄 | 52 |
| コンクリート | 0.8 |
| ガラス | 0.6 |
| 木材 | 0.16 |
| 空気 | 0.023 |
材料の熱伝導率の例
熱伝導解析の例では、3つの異なる熱伝導率を持つ材料内で熱がどのように流れるかを示しています。ケースは、上部の温度が一定で、下部の対流による熱損失があるように設定されています。
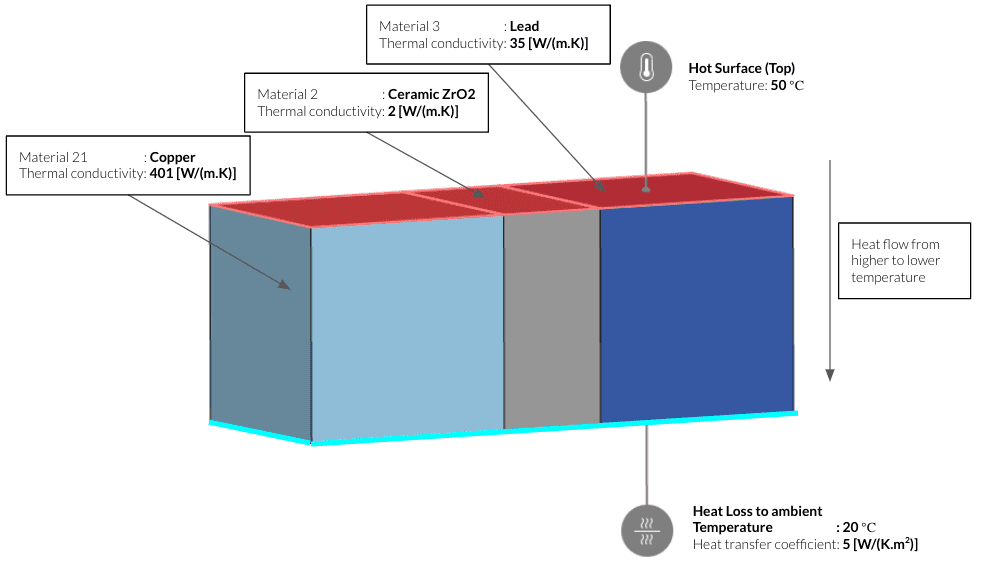
シミュレーションを50秒間実行すると、材料の熱伝導率によって熱流が変化することがわかります。左側の銅製のブロックは、熱伝導率の低い他の2つのブロックに比べて熱流が速いことがわかります。一方、セラミックでできた中央のブロックは、熱伝導率が非常に低いため、銅と鉛の間でほとんど絶縁体として機能します\(2 \frac{W}{\text {m.K}}\) 。
注: 建築物の熱性能では、熱伝導率と材料の厚さを組み合わせて断熱材のR値とU値を定義します。
主要パラメータ
温度
モデル内の各計算点における温度。スカラー値。
熱流束
モデル内の各計算点における熱流束。ベクトル値。グローバル成分X,Y,Zで表現。単位面積あたりの単位時間あたりのエネルギーの単位\(\frac{J}{\left(s\right)m^2}\) または単位面積あたりの単位電力\(\frac{W}{m^2}\) 。
熱伝達係数
熱流束と温度差を関係づける比例定数です[3]。熱伝達率は、材料の境界と外部環境との温度差に起因するため、一般的に材料の表面で計算されます。熱伝達率の単位は\(\frac{W}{\text{K.m}^2}\) です。
熱伝達率の一般的な定義は以下の通りです:
$$h=\frac{q}{\Delta T}$$
ここで
- \(h\): 熱伝達率
- \(q\): 熱流束\(\frac{W}{m^2}\)
- \(\Delta T\): 材料の表面と周囲の流体/環境との温度差
参考
- https://sciencenotes.org/heat-transfer-conduction-convection-radiation/
- https://scied.ucar.edu/learning-zone/earth-system/conduction
- https://en.wikipedia.org/wiki/Heat_transfer_coefficient
- https://www.engineeringtoolbox.com/thermal-conductivity-metals-d_858.html
- https://www.britannica.com/science/gas-state-of-matter/Thermal-conductivity
- https://en.wikipedia.org/wiki/Kinetic_theory_of_gases
熱伝導と合わせて読みたい
SimScale製品紹介資料ダウンロード

SimScaleの特徴と計算事例をまとめた資料を用意しております。