物理現象を数学的にモデル化する方法がわかったら、次のステップは数値領域を使用してそのモデルを新しい数値モデルに変換することです。カラフルな写真や美しいシミュレーションアニメーションがどのようにして得られるのか不思議に思ったことはありませんか?もしそうなら、ここがその場所です!この記事は、シミュレーションを行う際にユーザーが扱わなければならない数値計算の背景を説明しています。
複雑なアンダーカットを持つ丸い形状のような、高度に複雑な形状のシミュレーション結果の生成が困難であることは想像できます。流体中のせん断応力は、固体中の摩擦力に類似しており、流体の粘度に基づいて推定することができます。ご想像の通り、これは簡単に解決できるものではありません。これらの影響はすべて、今日まで科学が提供してきたモデルで正確に計算することは不可能です。しかし、非常に優れた数値モデルがあり、誤差が1%をはるかに下回る、非常に正確な近似結果を得ることができます。
数値モデル
数値モデルや数値手法は、解析的な解法が使えないような複雑な問題を扱うために設計された数学的ツールです。数値計算手法を導入する場合、方程式の離散化、ソルバーの適用、残差の収束の必要性など、すべてが正確なシミュレーションを成功させるために非常に重要になります。
数値計算の背景領域の一部であるこれらの数値技術は、プロセスの背後にある数式を理解し、より理解しやすい結果に解くために使用されます。これにより、より良い製品を作り、市場投入までの時間を大幅に短縮することができます。エンジニアリング・シミュレーションで使用される数値モデルの詳細については、こちらをご覧ください:
ナビエ・ストークス(Navier-Stokes / NS)方程式とは

ナビエ・ストークス(Navier-Stokes/NS)方程式は、流体の運動を支配する偏微分方程式です。この方程式は流体力学の基本方程式です。物理領域における流体の運動...
続きを読むLES (ラージ・エディ・シミュレーション) とは
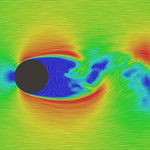
LES (ラージ・エディ・シミュレーション) はCFDの乱流モデルの一つです。RANSやDNSとの違い、特徴、活用例をわかりやすく解説します。乱流解析の鍵: LES ...
続きを読むレイノルズ数とは

レイノルズ数 (Re) は、流れの中で「慣性力」と「粘性力」のどちらが支配的かを表す無次元数です。主に、流れが層流か乱流かを判断するために用いられます。レイノルズ数は次の式で計算...
続きを読む境界条件とは | CAEとシミュレーションの基本要素をやさしく解説
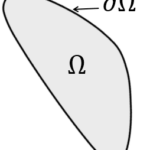
境界条件とは、CAE(シミュレーション技術)で解析対象の挙動を決めるために設定する条件のことです。境界値問題との関係や基本的な考え方をやさしく解説します。境界値問題とは、境界上の...
続きを読む輸送方程式とは
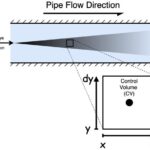
輸送方程式はスカラー量が流体内でどのように輸送されるかを記述するもので、パッシブスカラー、温度、運動量など多くのスカラーに適用されます。一般的な輸送方程式は以下の通りです:...
続きを読む