粘性とは、運動や変形に対する流体の内部抵抗を測定する、流体の集中的な特性です。

空気、水、油などの流体の流れの性質を決定するため、空気力学や貯留層工学などの分野で重要な役割を果たします。

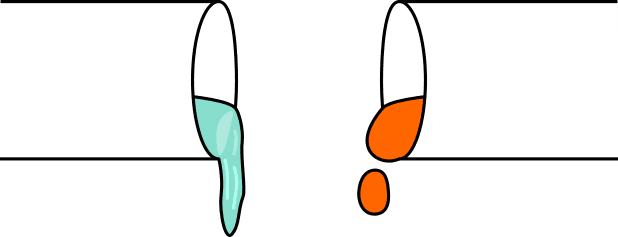
2つの流体の粘度を比較する日常的な例として、蜂蜜と牛乳の比較があります。直感的には、蜂蜜は牛乳よりも粘性があります。これは、下の図1のような実験で見ることができ、粘性の高い流体(右)は粘性の低い流体(左)よりも流れにくくなります。

図1: 粘性の高い流体(右)と低い流体(左)の流れの一例。高粘性流体は流動性が低い。

粘性の発見

流体力学の構造や定式化を含む数学の最も基本的な考え方は、17世紀後半から18世紀前半にかけて生まれました。乱流、不連続性、粘性などのより高度で複雑な概念は、19 世紀と 20 世紀に導入されました。

流体力学の分野が初めて科学的に定義されたのは、1687年のニュートンの「プリンキピア数学」です。

ニュートンの粘性の法則は、機械的応力を受けたときの流体のせん断応力とせん断速度の関係を記述したものです。

しかし、ニュートンは空気などの流体を粒子の凝集体として扱いました。流体力学の微分および連続形式が開発されたのは、レオンハルト・オイラーの時代になってからです$^1$ 。

しかし、多くの重要な疑問が現れ始めたのはニュートン以前のことです。クリスティアン・ホイヘンスは、流体内の物体の影響を研究することに関心を持っていました。彼は弾道を研究していたため、空気抵抗がどのように働くかを研究していました。相対運動する物体(その周囲を流体が取り囲んでいる)の力学を決定する問題は、抵抗の問題を通して表され、多くの側面で、粘性の研究と本質的に関連していました。

流体運動における粘性の重要性

粘性は、流体の運動を研究する際に非常に重要な特性です。粘性は、流体のせん断エネルギーによる隣接する流体層間の摩擦の損失を決定するのに役立ちます。言い換えれば、粘度は運動に対する流体の内部抵抗を決定します。粘度の高い流体は、粘度の低い流体よりも運動に対する抵抗が大きくなります。（たとえば、水よりも粘性の高いオイル）

流体力学の数学モデルは、主に質量保存、運動量の釣り合い、エネルギー保存と流体の構成関係に基づいています。上記の保存原理を組み合わせると、多くの粘性流体の運動を記述するために使用されるナビエ・ストークス方程式を形成することができます。

質量保存は次のように記述できます:

$$ \frac{\partial\rho}{\partial t}+\nabla\cdot\left(\rho\vec{u}\right)=0 \tag{1}$$

ここで、$\rho$ は空間と時間の関数としての質量密度であり、$\vec{u}$ は同じく空間と時間の関数としての速度です。これは質量保存則の強い定式化、あるいは連続の式として知られています。

運動量保存は$^2$ のように書くことができます:

$$ \frac{\partial\rho\vec{u}}{\partial t}+\nabla\cdot\left(\rho\vec{u}\otimes\vec{u}\right)+\nabla p(\rho)=\mu\nabla^2\vec{u}+\left(\lambda+\mu\right)\nabla\left(\nabla\cdot\vec{u}\right)+\vec{f} \tag{2}$$

ここで、$\mu$ はせん断粘性係数、$\lambda$ は粘性の第二係数、$\vec{f}$ は重力などの体力を表します。$\rho\cdot\vec{g}$ 、$\otimes$ は外積演算子で、$\vec{u}\otimes\vec{u}=\vec{u}\times\vec{u}^T$を表します。

これらの方程式は、ナビエ・ストークス方程式を形成します。$\lambda$ を$\eta-\frac{2}{3}\mu$ と近似するのが一般的で、$\eta$ はバルク粘度です。

一般に、流体が急激に圧縮または膨張しない非圧縮性の流れを考える場合、$\eta\approx 0$ と$\lambda\approx -\frac{2}{3}\mu$ はストークス仮説と呼ばれます。ストークス仮説は、ニュートン流体の場合、バルク粘度をゼロに設定できるというものです。この仮説は、低速(低マッハ数)で密度が変化する流れによく適用されます。

この場合、$\lambda$ は方程式から無視されるのが一般的です。また、バルク粘性係数は測定が難しく、文献で値を見つけることも困難です。速度の発散、$\nabla\cdot\vec{u}$ は通常非常に小さいため、バルク粘度を含む項全体は無視されるのが一般的です。

その結果、非圧縮性または等速流の場合、$\rho=1$ を仮定すると、速度の発散は完全に消失し、ナビエ・ストークス方程式は次のように簡略化されます:

$$ \nabla\cdot\vec{u}=0 \tag{3}$$

$$ \frac{\partial\vec{u}}{\partial t} + \nabla\cdot\left(\vec{u}\otimes\vec{u}\right) + \nabla p = \mu\nabla^2\vec{u}+\vec{f} \tag{4}$$

この系は非圧縮性ナビエ・ストークス方程式として知られています。

上記の方程式からわかるように、粘性は流体の力学を決定する上で重要な役割を果たします。非圧縮性ナビエ・ストークス方程式から、粘性は速度のラプラシアンに関連する拡散係数であることがわかります。

粘性の種類

粘度にはいくつかの種類があります。流体力学の分野で最も一般的に使用されるのは、せん断粘度(動的粘度)で、ここでは$\mu$ と表します。しかし、流れの物理学によっては、さまざまな粘度が対応する重要な役割を果たします。以下はその例です:

動粘性係数
粘性係数
見掛け粘度

動粘性係数

衝撃波や流体の急激な圧縮を含む現象を扱う場合、音の減衰などの重要な概念に関係するバルク粘度$\eta$ を無視することはできません。動粘度$\nu=\frac{\mu}{\rho}$ は、流体力学や伝熱学で頻繁に登場し、重力下の流れに関係します。

動粘性率を使用する一般的な式にレイノルズ数があります。これは運動量と流体の粘性力の関係を示す無次元数です。

粘性係数

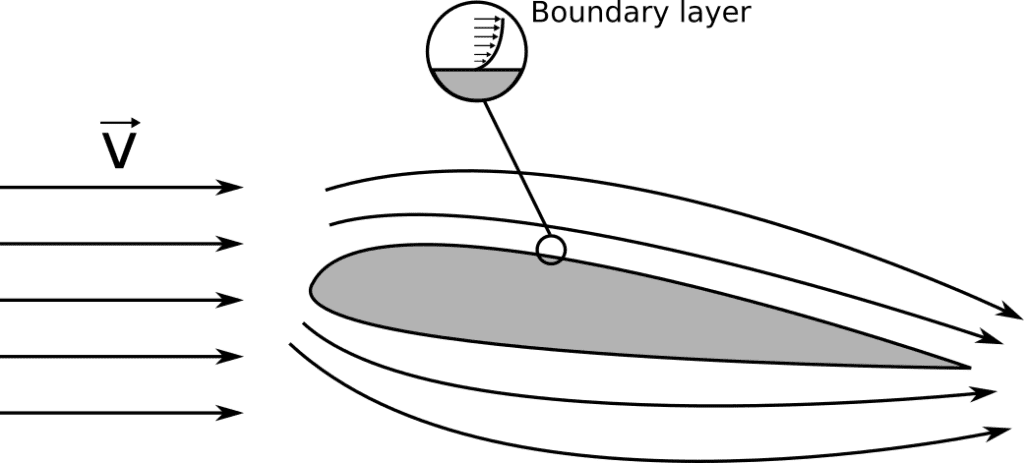
せん断粘度または粘性係数は、一般的に速度プロファイル実験で得られます。速度プロファイルの最も重要な例の 1 つは、$^1$ から引用した以下の図 2 に示すような境界層における速度プロファイルです。

翼のような物体の断面が流れの中で表現されています。境界層は、体と流体の相互作用において粘性の影響が最も大きくなる領域です。

図2: 翼を流れる流体と接触する翼の境界層

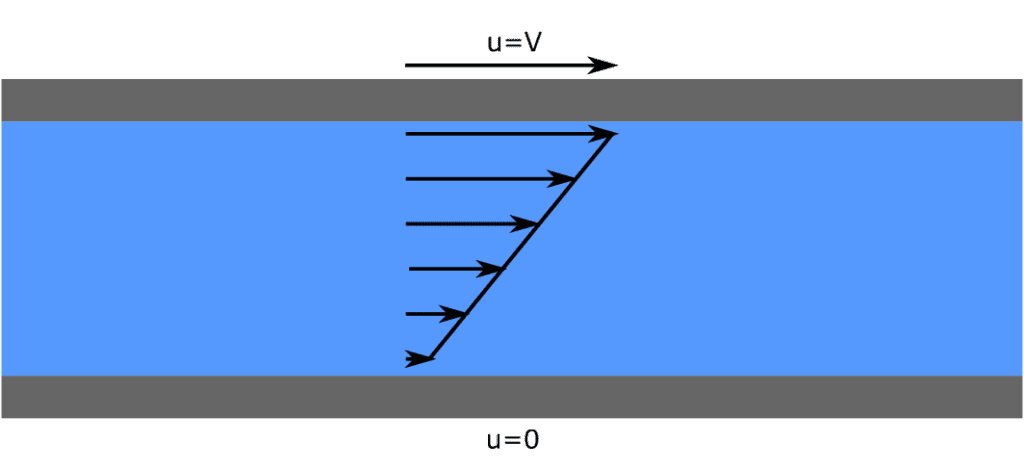
有名な速度プロファイルの実験では、2枚の平行で十分に大きなプレートが用いられ、接線速度はゼロでなく、法線速度はゼロで、2枚のプレートの間に流体が存在します。実験を簡単にするために、一方のプレートは固定され、もう一方のプレートは接線速度$u=V$ で接線方向に移動します。

流体には速度プロファイルが現れます。固定されたプレートに接する流体は速度がゼロになり、動くプレートに接する流体はプレートと同じ速度、すなわち$V$ になります。下の図3はこの実験を示しています。

図3: 2枚のプレートの間の流体の速度プロファイル

変形速度がせん断応力に直線的に比例するニュートン流体の場合、1 次元流れにおけるせん断粘度は次のように表すことができます$^3$ :

$$ \mu=\frac{\tau}{\frac{du}{dy}} \tag{5}$$

ここで、$\tau$ は移動プレートに接する流体層に作用するせん断応力、$\frac{du}{dy}$ は高さに対する速度の変化を示します。

固体に近くない領域では、慣性力と圧力が支配的であるため、粘性力を無視するのが一般的です。このような領域は非粘性流領域と呼ばれます。非粘性流体領域では、非粘性流体の運動を次のようにモデル化するオイラー系を採用するのが一般的です:

$$ \frac{\partial\rho}{\partial t} + \nabla\cdot\left(\rho\vec{u}\right)=0 \tag{6}$$

$$ \frac{\partial\rho\vec{u}}{\partial t} + \nabla\cdot\left(\rho\vec{u}\otimes\vec{u}\right)+\nabla p(\rho)=\vec{f} \tag{7}$$

見かけの粘度

上記のナビエ・ストークス方程式は、せん断応力と速度勾配の間の線形関係を運動量の釣り合い方程式に考慮して導かれています。しかし、非ニュートン流体の数学は非常に複雑になります。

このような場合、粘度は速度の関数になります。レオロジーの分野では、非ニュートン流体の流動を研究しており、粘度に関する他の多くのモデルが存在します$^4$ 。

非ニュートン流の場合、比率$\frac{\tau}{\frac{du}{dy}}$ は見かけの粘度と呼ばれ、一定とは限りません。せん断応力と変形速度の関係から、流体のタイプが分類されます。

例えば、見かけの粘度が変形速度とともに増加する流体はダイラタント流体と呼ばれ、見かけの粘度が変形速度とともに減少する流体は擬塑性流体と呼ばれます。

SimScaleでの計算事例

SimScaleパブリックプロジェクトライブラリでは、粘性流体の性質を探求する多くの計算実験を提供しています。ここでは、いくつかのシミュレーション例を紹介します。

シミュレーション1: 長いパイプを通る流体の流れ

滑りなし条件から始めると、下の図 4 は比較的長いパイプ内の断面速度プロフィールを示しています。境界での流速がゼロであることがわかります。

図4: 長いパイプ内を流れる流体の速度プロファイル

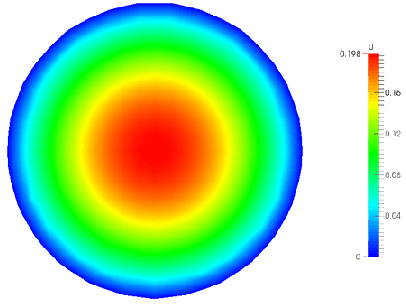
シミュレーション2: 翼形周りの圧縮性流れ

図5は、翼を解析する圧縮性気流を示しており、圧縮性流れを扱う場合のSimScaleの能力を示しています。

図5: 翼の周囲を流れる空気の速度場(前縁でゼロ速度(青色領域)を示す

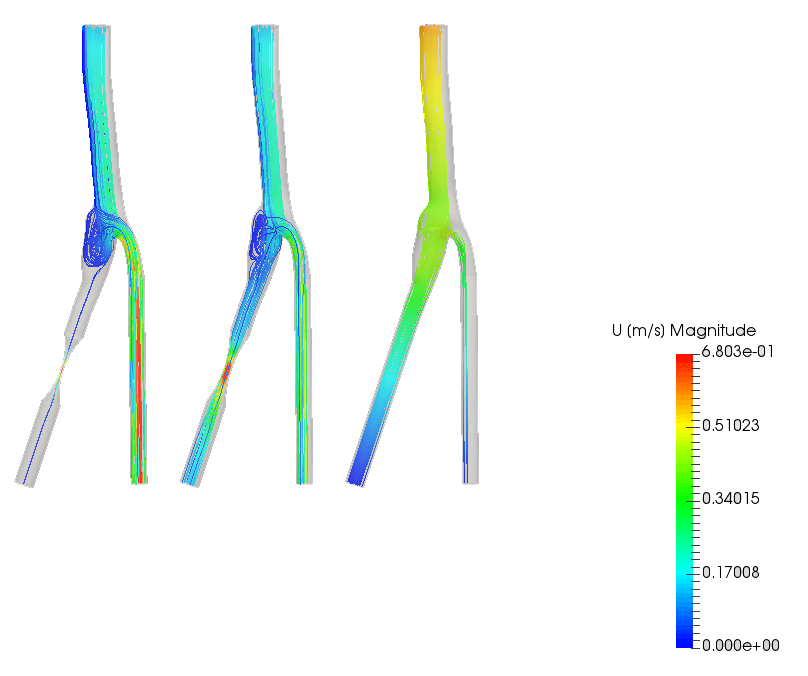
シミュレーション3: 動脈の分岐部を通過する血流

一般的な非ニュートン流体は血液です。SimScaleでは、血流をシミュレーションするプロジェクトを実施しています。

以下のプロジェクトでは、動脈分岐部内の血流をシミュレートし、3つの血管のケース(健康なもの、中程度に閉塞したもの、ひどく閉塞したもの)を比較します。

図6: 左から閉塞の程度が低くなるにつれて動脈内を流れる血液の速度場

参考

Calero, J. S., “The Genesis of Fluid Mechanics, 1640-1780”, 2008
Feireisl, E., Karper, T. G., Pokorny, M., “Mathematical Theory of Compressible Viscous Fluids”, 2016
Çengel, Y. A., “Fluid Mechanics: Fundamentals and Applications”, 2014
Irgens, F., “Rheology and Non-Newtonian Fluids”, 2014

2024年3月13日