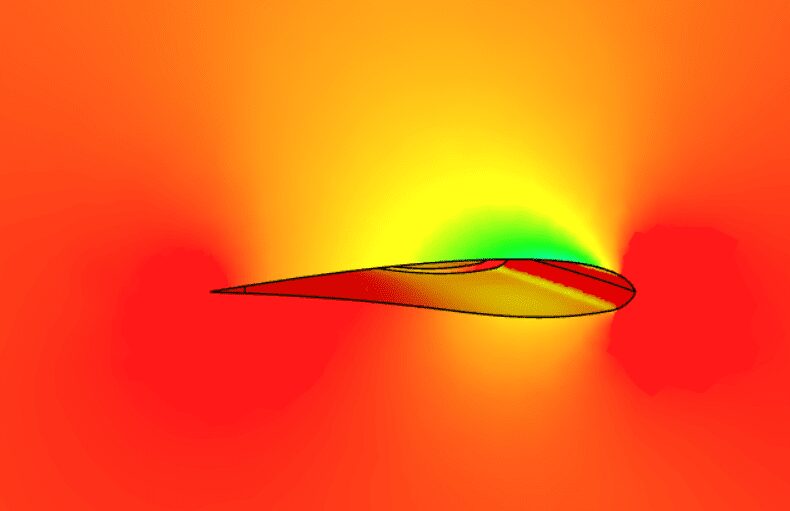
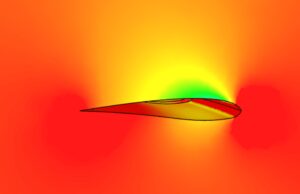
飛行機が空を飛ぶ仕組みには、揚力 (ようりょく)・抗力 (こうりょく)・ピッチという空気力学的な力が大きく関係しています。これらは、空気中を移動する翼型の形状や動きによって発生する力です。
特に、飛行機がどのように離陸し、空中を安定して飛び続けるのかを理解するには、これらの力が飛行中にどのように働いているかを知ることが重要です。
本記事では、翼型理論をベースに、揚力と抗力の発生メカニズム、そしてそれらがどのように飛行機や風力タービンの設計に応用されているのかを、図や例を交えながらわかりやすく解説します。
翼はどのようにして揚力を発生させるのか?
飛行機が空を飛ぶためには、揚力が必要です。この揚力を生み出すのが、翼型です。
翼型とは?
翼型とは、空気中を移動するときに効率よく揚力を発生させるために設計された形状です。飛行機の翼断面は、特有の湾曲を持った翼型になっています。この形状により、翼の上下に圧力差 (圧力勾配) を作ることによって、翼には上向きの力=揚力が発生します。
次の図のような飛行機を考えてみましょう。
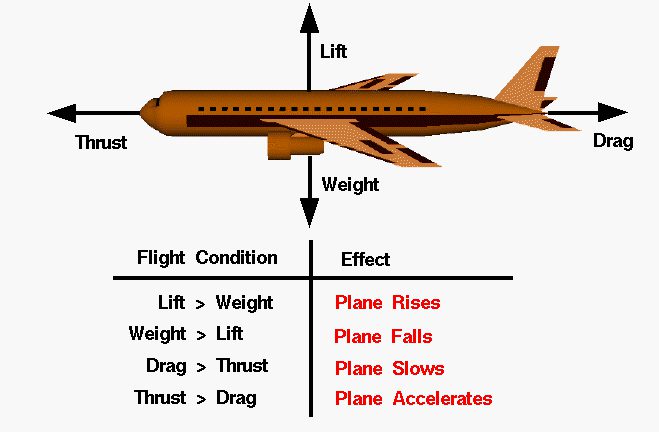
飛行中の飛行機に働く4つの力
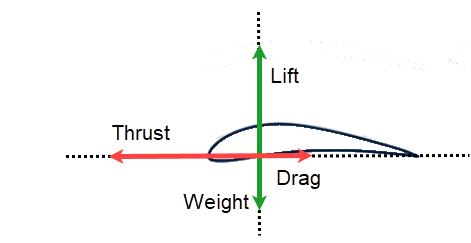
飛行中の飛行機には、主に次の4つの力が作用しています:
- 自重 (Weight): 重力による下向きの力
- 抗力 (Drag): 空気抵抗による後ろ向きの力
- 推力 (Thrust): エンジンなどによって生み出される前向きの力
- 揚力 (Lift): 翼が生み出す上向きの力
飛行機が空を飛び続けるためには、推力が抗力を上回り、揚力が自重を上回る必要があります。
翼の構造と揚力発生の理解
飛行機の翼は、複数の翼型が軸方向 (翼の幅方向) に沿って並んだ構造になっています。したがって、1つの翼型に働く力の仕組みを理解することで、翼全体が生み出す空力特性を把握することができます。
下図は単一の翼に作用する力の方向と大きさを示しています。この状態では、推力と揚力がそれぞれ抗力と重力より大きいため、飛行機は前に進みながら上昇する (加速・上昇) という運動をします。
翼に関する圧力分布
状態1は、翼型と相互作用する前の状態を表し、状態2は翼型と相互作用した後の状態を表します。図3は、関連する変数用語の模式図です:
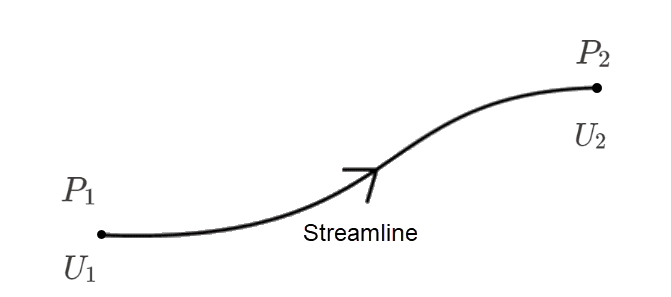
この流線に沿ってベルヌーイの方程式を適用すると、次のようになります:
$$ P_2 – P_1 = – \frac{1}{2} \rho(U_2^{2} – U_1^{2}) \tag{1} $$
ここで:
- \(P\): 静圧
- \(\rho\): 流体媒体の密度
- \(U\): 流体速度
翼の形状は、目的に応じて設計されています。これにより、翼型はその長さに沿って異なる流体速度を持つことができます。速度の変化は、ベルヌーイの方程式に従って、大気圧に対する圧力の変化につながります。
これらの対応する圧力荷重は、翼表面の法線方向に作用します。この力を表面全体で積分することで、単位表面積当たりに作用する総力を求めることができます。
翼の上面と下面
翼の上面を流れる空気の動きを、翼断面形状に沿った2次元的な視点で考えてみましょう。このとき、翼の最大厚さ付近 (最も曲率の大きい部分) では、空気の流れが加速することが分かります。
つまり、流速\(U_2\)は、自由流中の流速\(U_1\)を上回ります。この速度差により、静圧\(P_2\)は、動圧\(P_1\)よりも低くなります。
その結果、圧力差によって翼の上面には吸引力が生じ、翼型が上向きに引き上げられます (図4参照)。
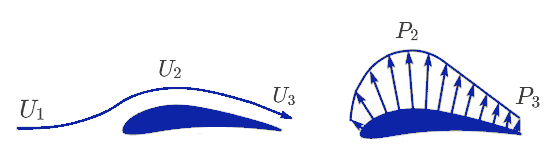
同様の方法で、翼型下面の圧力分布も解析することができます。
この翼型では、前縁付近の流れが加速し、それにより前縁を下方に引っ張る吸引圧が発生します。さらに、その後方では流れが減速し、圧力が上昇します。このときの圧力は大気圧より高くなり、翼型下面を上方に押し上げる力として作用します。
これらの圧力分布の結果、揚力に寄与する上向きの合力が発生します(図5参照)。
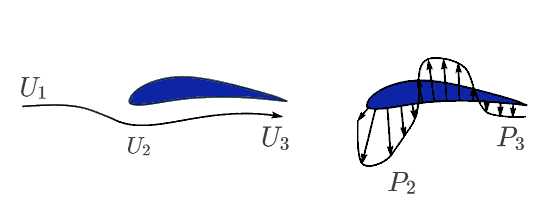
それぞれの翼型は、その形状の違いによって異なる空気の流れ (流線パターン) を持つことに注意してください。
翼の上面と下面に分布する圧力をそれぞれ積分することで、全体としての力の合成結果である総力ベクトル\(\vec F\)を求めることができます(図6参照)。
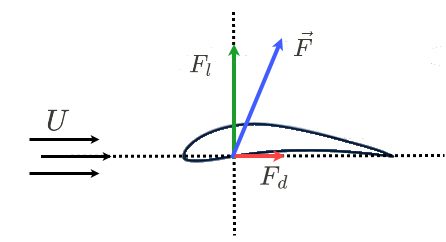
揚力とは?
揚力とは、全力ベクトル (\(\vec F\))のうち、物体の圧力中心を通り、流入する流れに対して垂直方向に働く成分のことを指します。
迎角がゼロの場合、揚力は通常、物体の重量と逆方向 (上向き)に働きます。
揚力は、物体が空気中を移動することによって生じる機械的な力であり、大きさと方向を持つベクトル量です。
揚力が発生するためには、以下の2つの要素が必要です:
- 流体の存在
固体物体と空気や水などの流体との間に相互作用があること。 - 運動の存在
揚力は、物体と流体との間に速度差があるとき、すなわち流体中を物体が運動しているときにのみ発生します。この運動によって、揚力だけでなく抗力 (ドラッグ) も生じます。特に、揚力の発生に伴って生じる抗力は誘導抗力 (inducted drag) と呼ばれます。
揚力の方程式
揚力は、流体密度、自由対流速度、翼の基準面積の関数です。また、揚力係数と呼ばれる無次元量も関係し、これは形状や速度の異なる翼の性能を比較するために使用されます。基本的に、揚力係数は、翼の形状、傾き (迎角)、および流れの状態が揚力にどのように影響するかを定量的に評価するために役立ちます。
揚力は次の式で表されます:
$$F_l = \frac{1}{2} \rho V^2 A C_l $$
ここで:
- \(F_l\) \([N]\): 指定された揚力方向の力の合成
- \(C_l\): 揚力係数 (無次元)
- \(ρ\) \([kg/m³]\): 流体の密度
- \(V\) \([m/s]\): 自由流速 (物体に対する相対速度)
- \(A\) \([m²]\): 基準面積 (通常は翼面積)
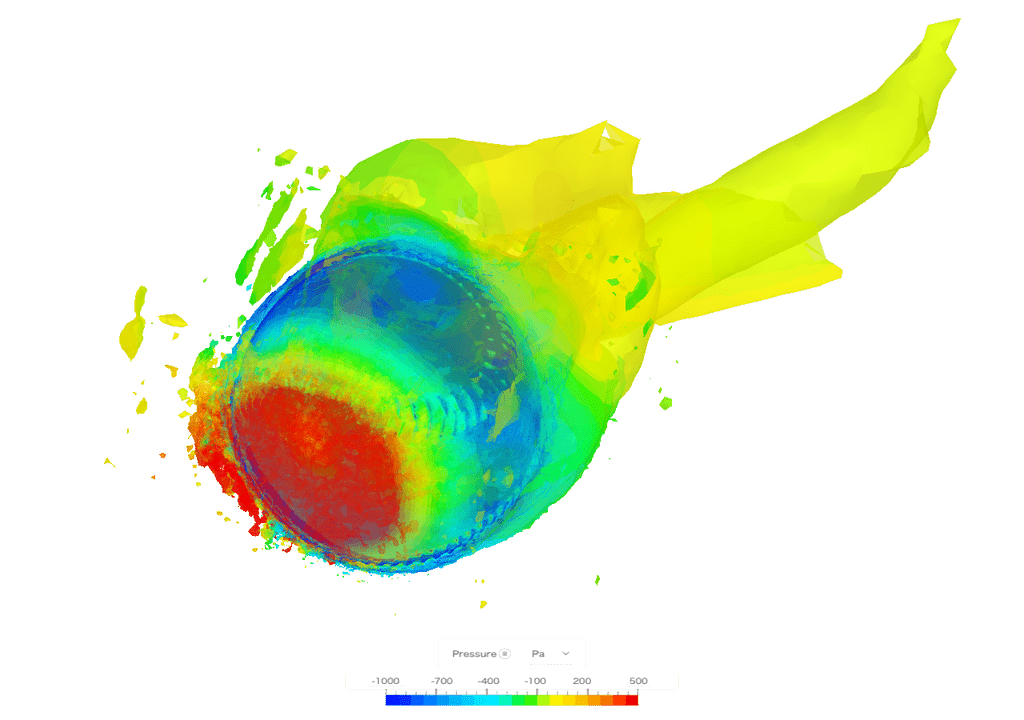
マグヌス効果 (回転に起因する揚力)
マグヌス効果とは、回転する物体の表面速度が非対称になることで圧力差が生じ、揚力が発生する流体力学的現象を指します。
野球のストレート (フォーシーム) の揚力や球質には、この効果が大きく寄与します。
抗力とは?
抗力とは、物体の圧力中心を通り、流入する流れの方向と平行に働く総力ベクトル(\(\vec F\) )の成分です。 迎角がゼロの場合、飛行機の推力とは逆に働きます(図1参照)。
しかし、抗力は固体と流体の速度差によって発生します。したがって、抗力が発生するのは、物体と流体の間に相対運動がある場合だけです。どちらか一方が存在しなければ、抗力は発生しません。
飛行物体には、2つの重要な抗力があります:
- 寄生抗力 (parasite drag):
寄生抗力とは、以下の2つの要素から構成される抗力です:- 形状抗力 (form drag):
物体の形状に依存する抗力であり、局所的な圧力を積分し、物体表面の投影面積と掛け合わせることで算出できます。 - 摩擦抗力 (skin friction drag):
これは、流体と物体の表面との直接的な相互作用により発生する抗力です。
接触面積が大きくなるほど、摩擦抗力も増大します。
- 形状抗力 (form drag):
- 誘導抗力 (inducted drag):
誘導抗力は、揚力の発生にともなって生じる抗力です。
飛行機では、翼端に発生する渦 (翼端渦) によって気流が乱され、翼まわりに旋回流 (渦流) が生じます。これにより、揚力の効率が低下し、同じ揚力を得るためにより大きな迎角が必要になります。
この現象は、風力タービンなど、揚力を利用するターボ機械にも見られます。
抗力の方程式
抗力は、流体密度、自由流速、翼の基準面積の関数でもあります。また、流体環境における翼の抵抗を測定するのに役立つ抗力係数と呼ばれる無次元量も関係します。
$$F_d = \frac{1}{2} \rho V^2 A C_d $$
ここで:
- \(F_d\) \([N]\): 指定された抗力方向の力の合計
- \(C_d\): 抗力係数
- \(ρ\) \([kg/m³]\): 流体の密度
- \(V\) \([m/s]\): 自由流速
- \(A\) \([m²]\): 基準面積
ピッチとは?
ピッチ(pitch)とは、航空機の機首がある軸を中心に上下に回転する動きのことです。
この動きは、飛行機の翼が発生させる揚力に大きく影響します。
図7を使って、片方の翼の端から重心を通り、もう一方の翼の端までの軌跡に沿った軸を想像してください。
その軸を中心とした航空機の回転運動が、ピッチ運動です。
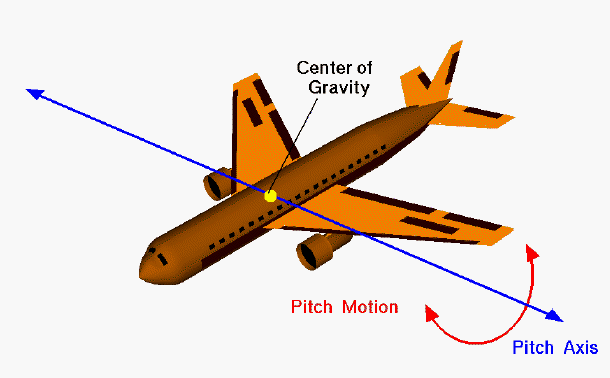
上向きのピッチング運動は、迎角 (angle of attack) の増加につながり、
その結果、総揚力が増加します (図10参照)。
これは、翼の下面のたわみに加えて、上面の流れが加速されるためです。
上向きの動きが大きくなるほど、翼が生み出す揚力も大きくなります。
しかしこの効果はある程度までで、やがて失速 (stall) が発生します (後述)。
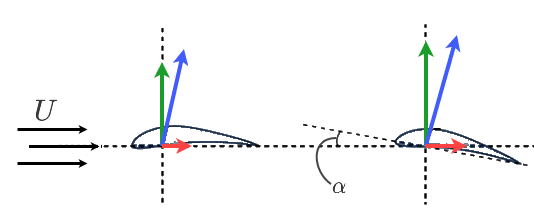
図8は、翼のピッチングと迎角の関係を示した模式図です。
迎角(angle of attack)が大きくなるにつれて、揚力と抗力の大きさがどのように変化するかに注目してください。
どちらの力も迎角の増加に伴って増加しますが、等しく増えるわけではありません。一般的に、揚力は抗力よりも速い割合で増加します。
その結果として、揚力抗力比(L/D比)は上昇します。これは、効率的な揚力の獲得につながる重要な指標です。
迎角とピッチ角
翼形では、迎え角は、入射する自由流体と前縁から後縁に延びる弦線との間の角度です。
一方、ピッチ角とは、弦線が任意の基準平面となす角度のことです。
この基準面は、飛行物体の平らな地面であったり、タービンのローターディスクの平面であったりします。
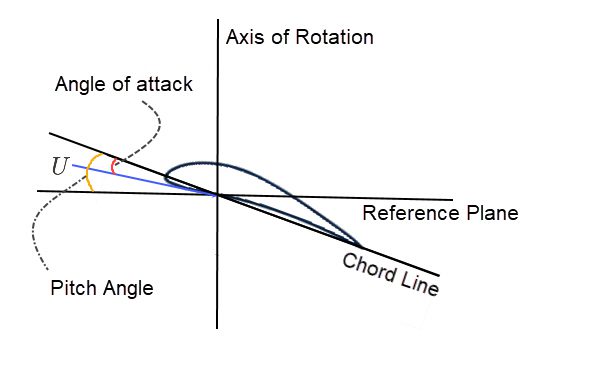
基準面によって、迎え角はピッチ角より大きくなることも、小さくなることも、同じになることもあります。
失速
迎え角が大きくなると、あるポイントまでは揚力と抗力の比が大きくなります。それ以上迎角を大きくすると、揚力が急激に減少し、抗力が急激に増加して失速状態になります。つまり、機体の重量を支えるだけの揚力が得られなくなり、機体が沈んでしまうのです。
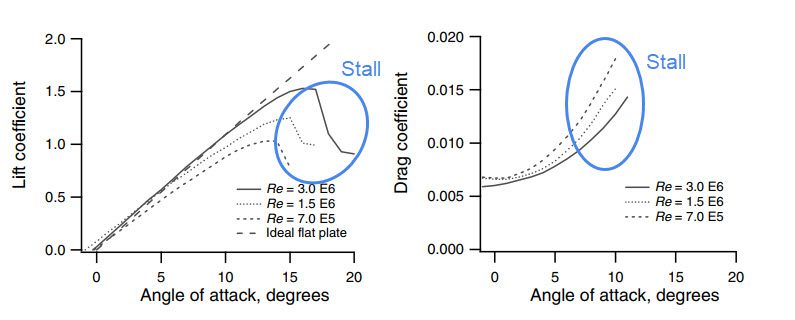
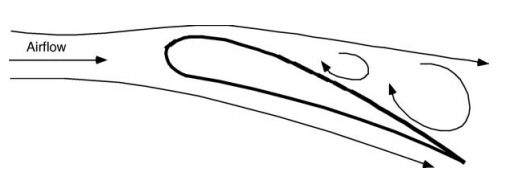
飛行機が失速することは、重量バランスをとるための揚力が不足することを意味するため、何としても避けなければなりません。失速現象はコンプレッサーでも見られ、ブレードの回転が不均一になることでローターの回転が遅くなり、同時にブレードの破損を引き起こします。
回転機械の揚力、抗力、ピッチ
水平軸または垂直軸の回転機械は、左右対称に配置された羽根を持つローターまたはインペラで構成されています。これには、風力タービン、ジェットエンジン、遠心ポンプ、コンプレッサーなどが含まれます。飛行機の翼のように、これらのブレードも一組の翼型から構成されています。
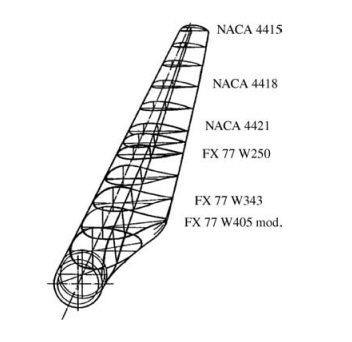
翼形はそれぞれ異なる機能を持っています。根元に近い翼型は構造剛性を確保し、中央と先端にある翼型は主に揚力に寄与します。
回転機械におけるピッチング
飛行機と回転機械の大きな違いは、回転機械の翼型は2つの要素から風/流体速度を受けるということです。
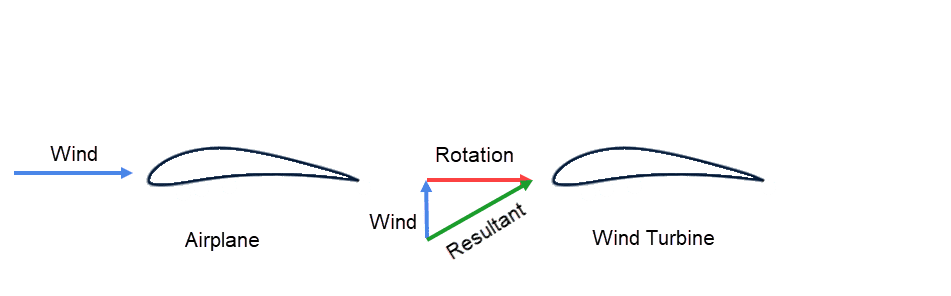
ブレードが下死点にあるとき、ローターの平面で上から観察した水平軸風力タービンのブレードを考えてみましょう。風は地面に対して水平に近づき、回転は時計回りです。このシナリオの上面図を図14に示します。さまざまな翼形がブレードのスパンに沿ってさまざまな角度でピッチングしていることに注目してください。
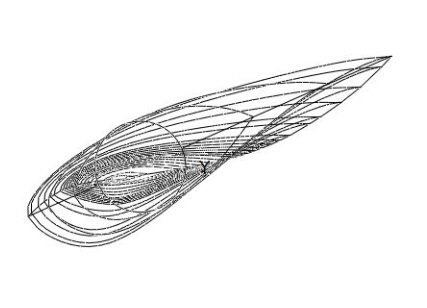
ブレードの各セクションにはそれぞれ異なる翼形があり、これは先に説明したように、各セクションが異なる目的を果たすことを意味します。スケルトンは、各翼形が異なるピッチ角を持っていることを明確に示しています。ルート/ハブに近いものはピッチングが大きく、先端に近いものはピッチングを小さくする必要があります。この説明は次のセクションで行います。
流れ角
流れ角\(\phi\) は、結果として生じる入射風速と回転平面がなす角度のことです。この流れ角は、ブレードの根元から先端に向かうにつれて小さくなります。これは、根元付近の接線速度が先端よりも低いためです。
$$ \vec v = \vec \omega \times \vec r $$
ここで:
- \(\vec v\): 接線速度
- \(\vec \omega\): 角速度
- \(\vec r\): ルート/ハブから離れる方向の半径方向ベクトル
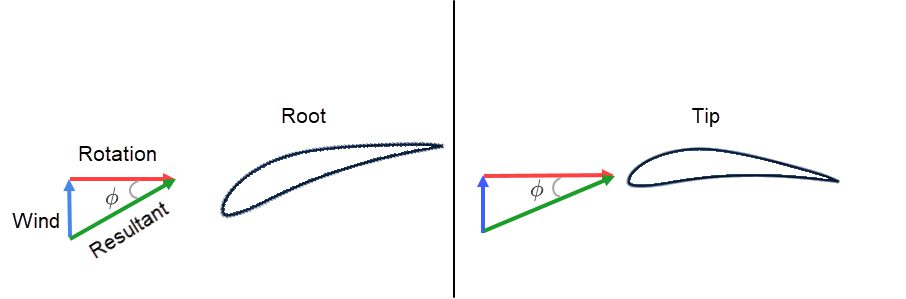
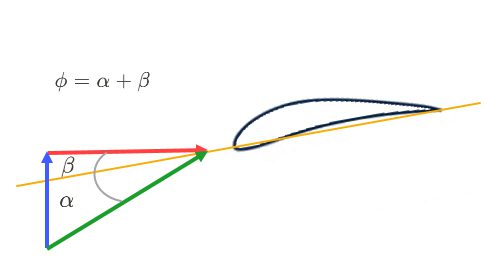
図16を単純に観察すると、この流れ角は迎え角とピッチ角の和であることがわかります。したがって次の式となります。
$$ \phi = \alpha + \beta $$
ここで:
- \(\phi\): 流れ角
- \(\alpha\): 迎え角
- \(\beta\): ピッチ角
迎え角の増加は失速につながるため、迎え角\(\alpha\) を所定の範囲内に保つことが最も重要になります。特に、流れ角\(\phi\) が大きいルート部では注意が必要です。これは、ピッチ角\(\beta\) を大きくすることで、ルート付近の翼型を過度にピッチングさせることで行います。
参考
- Beginner’s Guide to Aerodynamics”, Grc.nasa.gov, 2021.
- “Fluid Mechanics 101”, Youtube.com, 2018.
- J.F. Manwell, J.G. McGowan and A.L. Rogers, Wind Energy Explained. Chichester : John Wiley & Sons, 2011
揚力・抗力・ピッチと合わせて読みたい
SimScale製品紹介資料ダウンロード

SimScaleの特徴と計算事例をまとめた資料を用意しております。