CFD(Computational Fluid Dynamics)とは、計算能力を用いて支配方程式を解くことにより、物理的な流体の流れを数学的に予測するプロセスです。

エンジニアが新製品の設計を任された場合、例えば次のレースシーズンで勝つためのレーシングカーを設計する場合、空力学は設計の全体的な性能において重要な役割を果たします。とはいえ、空力性能はコンセプトの段階では簡単に定量化できません。

従来、エンジニアが設計を最適化する唯一の方法は、製品のプロトタイプで物理テストを実施することでした。コンピュータの台頭と(ムーアの法則により)増大し続ける計算能力により、CFDの分野は、現実世界の物理を予測するための一般的なツールとなっています。

CFDソフトウェアによる解析では、流体の流れとそれに関連する物理特性(速度、圧力、粘度、密度、温度など)が、定義された動作条件に基づいて計算されます。正確な物理解を得るために、これらの量は同時に計算されます。

商用またはオープンソースの CFD ツールでは、数学モデルと数値計算メソッドを使用して目的の流体物理を予測します．最も一般的なCFDツールは、ナビエ・ストークス(N-S)方程式に基づいています。Navier-Stokes方程式の項の大部分は一定のままですが、物理学に基づいて項を追加または削除することができます。例えば、熱伝導、相変化、化学反応などを考慮する必要がある場合は、支配方程式にさらに多くの項が導入されます。

CFD 解析を正確かつ成功させるためには、適切な運転条件、数値解析手法、物理を考慮することが非常に重要です．これが正しく行われれば、性能に関する洞察を迅速に得ることができ、最終的に性能が向上し、より効率的な最終製品を得ることができます。

SimScaleでは、ウェブブラウザですぐに管内流れから熱や冷却、気体と液体の混相流といった様々な現象の解析をおためしいただけます。

ウェブブラウザで流体解析をためす

CFDの歴史｜数値流体力学

古代から現在に至るまで、人類は流体の流れの観測結果を説明することに躍起になってきました。では、CFDの歴史は古いのでしょうか？CFDの分野には大きな欠点があります。それは、計算コストが非常に高いということであり、そのため、コンピューティングパワーがコストと性能において大幅に改善されるまでは、進歩することができませんでした。このような事態が起こるまで、科学者やエンジニアは、計算コストを削減する数学的モデルや数値計算手法の改良に重点を置いてきました。

計算流体力学の簡単なストーリーを以下に示します:

1910年まで

数学モデルと数値計算手法の改良
1910 - 1940:

手計算に基づく数値解を生成するためのモデルと手法の統合†
1940 - 1950:

初期のコンピュータ(ENIAC)によるコンピュータベースの計算への移行†
1953年、川口による機械式卓上計算機での円柱周りの流れの解法[M. Kawaguti, “Numerical Solution of the NS Equations for the Flow Around a Circular Cylinder at Reynolds Number 40”, 1953, Journal of Phy.Soc. Japan, vol. 8, pp. 747-757]
1950 - 1960:

米国ロスアラモス国立研究所による、Navier-Stokes方程式に基づく流体流れをモデル化するためのコンピュータを使用した初期研究。渦度の評価 - 流線関数法†。2次元、非定常、非圧縮性流れに対する世界初の実装†。
1960 - 1970:

1967年、HessとSmithにより、3次元物体の計算解析に関する最初の科学論文 "Calculation of potential flow about arbitrary bodies "が発表†商用コードの生成。k-ε乱流モデル、Arbitrary Lagrangian-Eulerian、SIMPLEアルゴリズムなど、現在も広く利用されている様々な手法の貢献†。
1970 - 1980:

ボーイング社、NASA、その他数社によって作成されたコードが発表され、潜水艦、水上船舶、自動車、ヘリコプター、航空機など、さまざまな用途で使用され始めた†。
1980 - 1990年:

Jamesonらによる3次元の遷音速流の正確な解法の改善。学術界と産業界の双方を通じて商用コードの実装が開始[Jameson, A., Schmidt, W. and Turkel, E., “Numerical Solution of the Euler Equations by Finite Volume Methods”]
1990 - 現在:

インフォマティクスの徹底的な発展: 事実上あらゆる分野でCFDが世界的に利用。

ナビエ・ストークス方程式の台頭

すべての理論的流体力学モデルの中心的な数学的記述は、粘性が支配的な流れ(英語)の運動を記述するナビエ-ストークス方程式(英語)によって与えられます。その発見の歴史は非常に興味深いものです。

有名なナヴィエ・ストークス方程式は、クロード＝ルイ・ナヴィエ(1785-1836)とジョージ・ガブリエル・ストークス(1819-1903)によって生み出されました。当初、クロード=ルイ・ナヴィエは、1822年まで方程式の部分断面に関する研究を行っていました。その後、ジョージ・ガブリエル・ストークスが1845年に方程式を調整し、最終的に完成させました[9] 。

CFD の支配方程式

熱流体試験の主要な構造は，流体の物理的性質の保存則に基づく支配方程式によって指示されます．基本方程式は下記の3つの支配方程式[10,11]です:

質量保存則：連続の式
運動量保存則：ニュートンの第二法則
エネルギー保存則：熱力学第一法則またはエネルギー方程式

これらの原則は、質量、運動量、エネルギーが閉じた系内で安定した定数であることを示しています。つまり、すべてが保存されなければなりません。

熱変化を伴う流体の流れの調査は、特定の物理的特性に依存しています。これらの3つの基本保存式から同時に求めなければならない3つの未知数は、速度$v$、圧力$p$、温度$T$です。しかし、$p$と$T$は、必要とされる2つの独立した熱力学変数と考えられています。

密度$\rho$、エンタルピー$h$ 、粘性$\mu$ 、熱伝導率$k$ の4つの熱力学変数も保存方程式の最終形に含まれます。これらの4つの特性は、$p$ と$T$ の値によって一意に決まります。

流体の流れは、$\vec{v}$ 、$p$ 、$T$ の値を評価する必要があります。さらに、運動学的性質に基づく流体流の観測方法は基本的な問題です。流体の動きは、ラグランジュ法やオイラー法で調べることができます。

流体運動のラグランジュ記述は、特性を検出するのに十分な大きさの流体粒子を追跡する理論に基づいています。時刻$t_0$ における初期座標と、時刻$t_1$ における同じ粒子の座標を調べる必要があります。
オイラー法では、経路を横切って特定の粒子を追跡する代わりに、速度場を空間と時間の関数として調べます。

このミサイルの例は2つの方法を説明した図です。

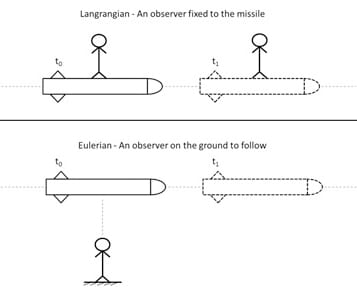
ラグランジュ型：
領域の始点にあるすべての点を取り上げ、終点に到達するまでその経路をたどります。

オイラー型：
流体内の窓(制御体積)を考え、この体積内の流れを評価します。

連続の式

質量保存則は次のように計算されます:

$$ \frac{D\rho}{Dt} +\rho (\boldsymbol{\nabla} \cdot \boldsymbol{v}) =0 \tag{1}$$

ここで、$\rho$ は密度、$\boldsymbol{v}$ は速度、$\boldsymbol{\nabla}$ は勾配演算子です。

$$ \boldsymbol{\nabla} = \boldsymbol{i} \frac{\partial}{\partial x} + \boldsymbol{j} \frac{\partial}{\partial y} + \boldsymbol{k} \frac{\partial}{\partial z} \tag{2}$$

密度が一定の場合、流れは非圧縮性であると仮定され、連続方程式は次のようになります:

$$ \frac{D\rho}{Dt} = 0 $$

$$\boldsymbol{\nabla} \cdot \boldsymbol{v} = \frac{\partial u}{\partial x} + \frac{\partial v}{\partial y} + \frac{\partial w}{\partial z} = 0 \tag{3}$$

ナビエ・ストークス方程式

ナビエ・ストークス方程式と呼ばれる運動量保存式は次式で与えられます:

$$ \frac{\partial}{\partial t}(\rho\boldsymbol{v}) + \boldsymbol{\nabla}\cdot (\rho\boldsymbol{v}\boldsymbol{v}) = -\boldsymbol{\nabla}p + \boldsymbol{\nabla}\cdot\boldsymbol{\tau} + \rho\boldsymbol{g} \tag{4}$$

ここで、$p$ は静圧、$\boldsymbol{\tau}$ は粘性応力テンソル、$\rho \boldsymbol{g}$ は単位体積あたりの重力。ここで左から順に、I: 非定常項、II: 対流項、III: 圧力項、IV: 粘性項、V: 外力項です。

粘性応力テンソル$\boldsymbol{\tau}$ は、ストークスの仮説に従って以下のように指定できます:

$$ \tau_{ij} = \mu \frac{\partial v_i}{\partial x_j} + \frac{\partial v_j}{\partial x_i} – \frac{2}{3}(\nabla \cdot \boldsymbol{v}) \delta_{ij} \tag{5}$$

流体が非圧縮性で粘性係数$\mu$が一定であると仮定すると、ナビエ・ストークス方程式は次のように簡略化されます:

$$ \rho \frac{D\boldsymbol{v}}{Dt} = -\boldsymbol{\nabla} p + \mu \nabla^2 \boldsymbol{v} + \rho \boldsymbol{g} \tag{6}$$

ニュートンの熱力学第一法則

エネルギー保存は熱力学の第一法則であり、系に加えられる仕事と熱の合計が系内のエネルギーの増加をもたらすことを述べています:

$$ dE_t=dQ + dW \tag{7}$$

ここで、$dQ$ は系に加えられた熱、$dW$ は系に加えられた仕事、$dE_t$ は系の総エネルギーの増分です。エネルギー方程式の一般的なタイプの1つは次のとおりです:

$$ \rho\frac{\partial h}{\partial t} + \rho\boldsymbol{\nabla}\cdot (h\boldsymbol{v}) = -\frac{\partial p}{\partial t} + \boldsymbol{\nabla}\cdot (k\boldsymbol{\nabla}T) + \phi \tag{8}$$

ここで左から順に、I: 非定常項、II: 対流項、III: 圧力項、IV: 熱流束項 、V: 熱源項です。

偏微分方程式

数学モデルは、直接または間接的にプロセス全体に関与する輸送パラメータ間の相互関係を与えるだけです。これらの方程式のすべての項が物理現象に相対的な影響を与えるとしても、パラメータの変化は、微分方程式、ベクトル、テンソル表記からなる数値解法を通して同時に考慮されなければなりません。

偏微分方程式は複数の変数から構成され、"$\partial$"で示されます。方程式の導出が"$d$"で行われる場合、これらの方程式は単一の変数とその導出を含む常微分方程式と呼ばれます。偏微分方程式は解を得るために微分演算子($\partial$)を代数演算子に変換します。熱伝導、流体力学、音響学、電子工学、量子力学などは、解を生成するために偏微分方程式が多用される分野です。

常微分方程式の例

$$ \frac{d^2 x}{dt^2} = x \rightarrow x(t) \quad \text{where T is the single variable} \tag{9}$$

偏微分方程式の例

$$ \frac{\partial f}{\partial x} + \frac{\partial f}{\partial y} = 5 \rightarrow f(x,y) \quad \text{where both x and y are the variables} \tag{10}$$

支配方程式の解を求める上で、偏微分方程式はどのような意味を持つのでしょうか。この問いに答えるために、まずいくつかの偏微分方程式の基本的な構造を調べ、意味づけをします。例えば

$$ \frac{\partial^2 f}{\partial x^2} + \frac{\partial^2 f}{\partial y^2} = 0 \rightarrow f(x,y) \rightarrow \text{Laplace Equation} \tag{11}$$

式(3)と式(11)を比較すると、連続の式のラプラス方程式がわかります。次のステップは何でしょうか？このラプラシアンは何を意味するのでしょうか？この巨大な方程式を解き始めるために必要な次のステップは離散化です。

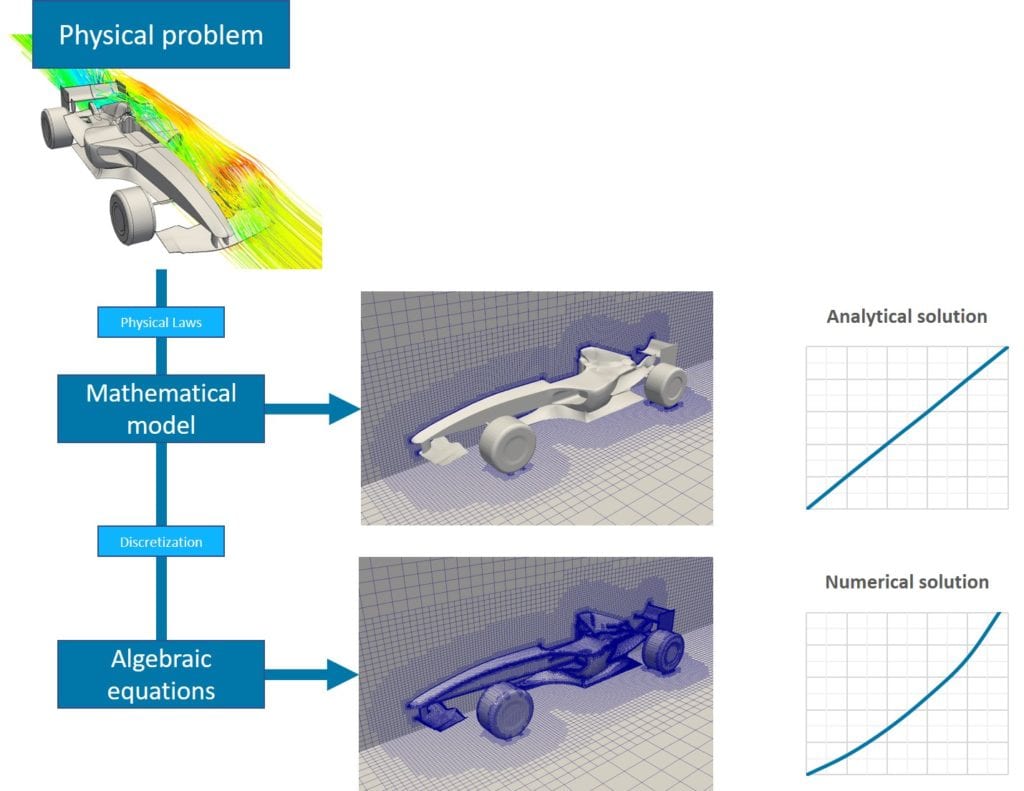
離散化

数値解法は、解析的手法では解けない複雑な問題の近似解を得るために用いられる離散化ベースの手法です。図4に見られるように、離散化を行わない解法では、厳密ではあるが単純な解析解が得られるだけです。

さらに、数値解の精度は離散化の質に大きく依存します。離散化には、有限差分法、有限体積法、有限要素法、スペクトル(要素)法、境界要素法などがあります。

メッシュの収束

解析を実施するために，解析領域はセルと呼ばれる複数のサブ領域に分割されます．これらのセルを組み合わせた計算構造をメッシュと呼びます。

メッシュ生成は、各セルに線形性があるという仮定の下で数学モデルを適用するために、領域を小さなセルまたは要素に離散化するプロセスです。これは、解く必要のある変数の挙動が各セル内で線形であると仮定できることを保証する必要があることを意味します。この要件はまた、予測される物性が非常に変動的であると疑われる領域では、より細かいメッシュが必要であることを意味します。メッシュについてより詳しくお知りになりたい方は、メッシュとは(英語)をお読みください。

メッシュエラーとメッシュ独立性研究

メッシュに起因するエラーは、不正確な解やシミュレーションの完全な失敗につながる一般的な問題です。これは、メッシュが粗すぎるために、大きく粗いセルの領域内で流れの物理が捕捉されないために起こります。このため、メッシュが解に具体的な影響を与えないことを確認するために、メッシュ独立性調査を実施する必要があります。メッシュ独立性調査の例を以下に示します:

形状を正確にとらえ、目視で十分なセルとメッシュ密度を持つように見える初期メッシュを生成します。
メッシュを再生成し、セル数を増やし、関心のある領域のメッシュ密度を高めます。CFD解析を再度実施し、結果を比較します。例えば、流路を流れる内部流の解析の場合、臨界領域での圧力損失を比較することで、メッシュ感度を測定することができます。
結果と主要な物理特性(圧力損失、最大速度など)が前回のメッシュと CFD 解析で満足のいく結果に収束するまで、メッシュを改良し続けます。

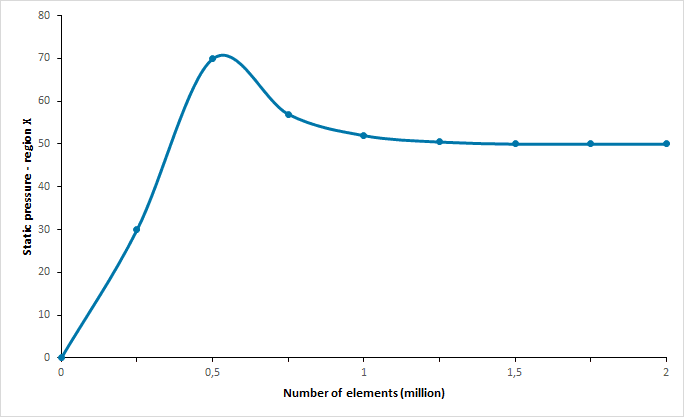
こうすることで、メッシュ構造に基づく誤差を排除し、最適な要素数を達成して効率的な計算を行うことができます。図6はメッシュ要素数の増加による静圧変化を調べたものです。図6によれば、信頼性の高い検討を行うためには、100万要素程度あれば十分であったと考えられます。

数値流体力学における収束

彫刻を作るには、最初から最終的な製品を想像する能力を持った、非常に才能のある芸術家が必要です。つまり、彫刻は最初はただの岩のかけらですが、最後には特別な芸術作品になるかもしれません。材料を徐々に削り取るプロセスは、望ましい最終的な形状を得るための中心的な作業です。

CFDもまた、徐々に変化する結果に依存し、最終的に最終的な解決策を導き出すという、似たようなプロセスを持っています。CFD解析では、芸術家が石の塊から始めるのと同じように、初期推測を出発点とします。数値計算の繰り返しにより、解の場は初期推測から最終的な持続する流れ場へと変化します。数値計算の反復は最終的な解に到達するためのものですが、結果の精度は、正確な解を得るためのメッシュに完全に依存していることに留意してください。

収束は計算解析にとって最も重要な問題です。流体の動きには、乱流、相変化、物質移動など、さまざまな複雑なモデルを持つ非線形モデルがあり、収束はそれらに大きく影響されます。解析的解法とは別に、数値解法は前段階の誤差を減らすことによって結果を得る反復スキームをとります。最後の2つの解の差が誤差となります。絶対誤差が減少すると、結果の信頼性が増し、安定した解に収束します。

解が収束するのはいつですか？

解の場が変化しなくなるまで、さらに繰り返しながら解き続ける必要があります。これは定常シミュレーションでも非定常シミュレーションでも同じです。非定常シミュレーションでは、定常シミュレーションと同じように、各時間ステップで収束を得る必要があります。

収束の基準は何ですか？

方程式の残差は、彫刻の石の残骸のように、反復ごとに変化します。反復がある閾値まで下がると、収束が達成されます。これは、芸術家が彫刻から最後の小さな石を取り除くのに似ています。収束について、さらにいくつかの重要な事実があります:

初期条件、緩和係数、クーラン数などのパラメータによって変化します。
解が常に正しいとは限りませんが、解が収束することはあります。不十分な数学モデルやメッシュは、不正確でありながら収束した結果をもたらすことがあります。
適切なメッシュ品質、メッシュの精密化、1次から2次の離散化スキームの使用など、いくつかの方法で安定化させることができます。
曖昧さを避けるために必要であれば、解が反復可能であることを確認します。

計算流体力学の応用

CFDは、流体の流れを伴うあらゆるアプリケーションで使用できます。例えば、円柱上の流れは、大学レベルの流体コースで教えられる典型的な学術的な例です。同じ現象は、図 7 に見られるように、大気中の雲の動きでも観察することができます。

非圧縮流れと圧縮流れ

圧縮性が無視できない要因になる場合，この種の解析は，非常にロバストで正確な方法で圧縮性流れの解を求めるのに役立ちます。一例として、ラージ・エディ・シミュレーションによる円柱周りの流れの解析が挙げられます。

層流と乱流

密度、粘度、流速などの流れの特性によって、流れは層流(英語)と乱流(英語)のどちらかに分類されます。しかし、例外もあります。例えば、暖かい照明からの自然対流は層流とみなされます。乱流シミュレーションは、支配方程式に含まれる項が多くなるため、計算コストが若干高くなります。このバルブは乱流解析の一例です。