フォンミーゼス応力とは、与えられた材料が降伏するか破壊するかを決定するために使用される値です。主に金属などの延性材料に用いられます。フォンミーゼス降伏基準は、荷重を受けた材料のフォンミーゼス応力が、単純引張を受けた同じ材料の降伏限界以上であれば、その材料は降伏するというものです。

フォンミーゼス応力の歴史

弾性理論の歴史は、17世紀のロバート・フック(Robert Hooke)$^1$ 、バネの変形と梁の変位に関する基本的な概念を探求した研究から始まったと一般に考えられています。しかし、弾性理論の研究の理由は工学だけではありません。その研究は、エーテル$^2$ の性質と理論の解釈の試みとも関連していたからです。

物体の弾性に関する定量的かつ数学的な理論が、連続体力学とともに誕生したのは19世紀のことです。これにより、弾性現象をモデル化する際に積分学や微分学が使えるようになりました。連続体力学は、媒質の均質化を前提としており、微視的な揺らぎが平均化され、媒質をモデル化した連続場が得られます。従って、媒質が占める時間の各瞬間と空間の各点に、時間的粒子が存在することになります。

連続体力学の基本概念から派生した理論や概念は数多くあります。そのひとつが最大歪みエネルギー理論で、ゴムベアリングや他の延性材料への応用など、多くの分野で応用されています。これを最初に提唱したのは1904年のヒューバートで、その後フォン・ミーゼスが1913年にさらに発展させました$^3$ 。

最大歪みエネルギー理論によると、降伏は歪みエネルギーが臨界値に達したときに起こります。この臨界値は材料固有のもので、簡単な引張試験で簡単に求めることができます。

降伏とは

初期平衡状態または変形していない状態の物体に、体内力または表面力が加わると、物体は新しい力学的平衡状態または変形状態に達するまで、それに応じて変形します。体内力は重力などの力場の結果であり、表面力は他の物体との接触によって物体に加えられる力です。

応力と呼ばれる外力と、ひずみと呼ばれる変形との関係は、応力-ひずみ線図と呼ばれます。これらの関係は、物体を構成する材料の特性を表しており、構成方程式としても知られています。

下の図([4]から引用)は、軟鋼梁の一軸引張のひずみ応答を調べたときに得られた曲線を示しています。これらは、なぜフォンミーゼスが重要なのかを理解するのに役立ちます。各重視点の説明は以下の通りです:

弾性限界
弾性限界は、応力とひずみの過程でエネルギーが失われない領域を定義します。つまり、弾性限界を超えない過程は可逆的です。この限界は降伏応力とも呼ばれます。この限界を超えると、変形は弾性的でなくなり塑性的となり、変形には不可逆的な部分が含まれます。ここでは、弾性限界の応力値を$S_y$ として使用します。
上降伏と下降伏
軟鋼が塑性域にあり、上降伏点と呼ばれる臨界点に達すると、そこから再び変形に抵抗し始めるまで一定の応力で変形が起こる下降伏点まで急速に低下します。
破断応力
破断とは、応力によって物体が分離することです。従って、この時点で本体の破壊が予想されます。軟鋼のように、大きな塑性変形の後にのみ破断する性質を持つ材料は延性と呼ばれます。ここに示した破壊は延性破壊と呼ばれるものです。延性破壊の見分け方は、下図のような曲線を描いているときです。これは、材料が薄くなるにつれて、破断応力点で突然破断するまで、より大きな圧力がかかることを意味します。

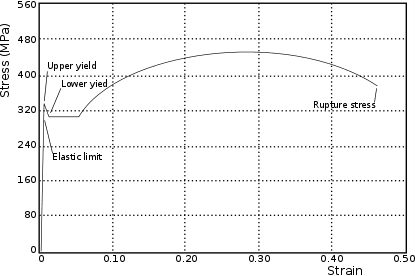
図1: 一軸引張時の臨界段階を示す軟鋼の応力-ひずみ線図

このダイアグラムは、下図に示すように、多くの材料で一般的に近似されています:

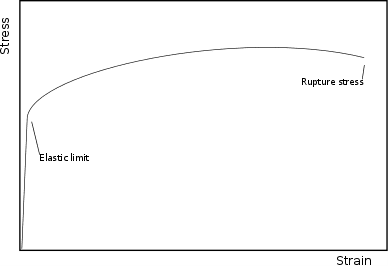
図2: 一軸引張時の応力-ひずみ線図の一般的な近似

フォンミーゼス降伏基準

前述した弾性限界は、単純な引張または一軸応力実験に基づいています。しかし、最大歪みエネルギー理論は、材料、特に延性材料が、非単純引張応力または非一軸応力を加えた場合に異なる挙動を示すことが観察されたことに端を発します。材料は、単純引張実験で観察された値よりもはるかに大きな抵抗値を示すようになったのです。これが、応力テンソルを完全に含む新しい理論の開発につながりました。

フォンミーゼス応力は、金属やその他の延性材料に広く使われている降伏の基準です。これは、物体に作用する応力成分がこの閾値より大きい場合に物体が降伏するとしています。$^4$ :

$$ \frac{1}{6}[(\tau_{11}-\tau_{22})^2 + (\tau_{22}-\tau_{33})^2 + (\tau_{33}-\tau_{11})^2 + 6(\tau^2_{12}+\tau^2_{23}+\tau^2_{13})]=k^2 \tag{1}$$

定数$k$ は実験によって定義され、$\tau$ は応力テンソルです。$k$ を定義するための一般的な実験は一軸応力から行われ、上記の式は次のようになります:

$$ \frac{\tau^2_y}{3}=k^2 \tag{2}$$

$\tau_y$ が単純引張弾性限界$S_y$ に達すれば、上式は次のようになります:

$$ \frac{S_y^2}{3}=k^2 \tag{3}$$

これは最初の式に代入できます:

$$ \frac{1}{6}[(\tau_{11}-\tau_{22})^2 + (\tau_{22}-\tau_{33})^2 + (\tau_{33}-\tau_{11})^2 + 6(\tau^2_{12}+\tau^2_{23}+\tau^2_{13})]=\frac{S_y^2}{3} \tag{4}$$

あるいは、最後に

$$ \sqrt{\frac{(\tau_{11}-\tau_{22})^2 + (\tau_{22}-\tau_{33})^2 + (\tau_{33}-\tau_{11})^2 + 6(\tau^2_{12}+\tau^2_{23}+\tau^2_{13})}{2}}=S_y \tag{5}$$

フォンミーゼス応力$\tau_v$ は次のように定義されます:

$$ \tau_v^2=3k^2 \tag{6}$$

従って、フォンミーゼスの降伏基準は一般的に次のように書き直されます:

$$ \tau_v\geq{S_y} \tag{7}$$

すなわち、フォンミーゼス応力が単純引張降伏限界応力より大きければ、その材料は降伏すると考えられます。

フォンミーゼス応力は真の応力ではありません。一般的な三次元応力と一軸応力降伏限界応力との比較を可能にする理論値です。

フォンミーゼス降伏基準は八面体降伏基準$^5$ としても知られています。これは、八面体平面(すなわち、法線が座標系と等しい角度をなす八面体を形成する8つの平面)に作用するせん断応力が次のように書けることによります:

$$ \frac{1}{3}\sqrt{(\tau_1-\tau_2)^2 + (\tau_2-\tau_3)^2 + (\tau_3-\tau_1)^2}=\tau_{oct} \tag{8}$$

一軸または単純引張の場合、次のように簡略化されます:

$$ \frac{\sqrt2}{3}\tau_y=\tau_{oct} \tag{9}$$

$\tau_y$ が単純引張弾性限界$S_y$ に達すれば、上式は次のようになります:

$$ \frac{\sqrt2}{3}S_y=\tau_{oct} \tag{10}$$

そして、この結果を八面体の応力式に当てはめると、次のようになります:

$$ \sqrt{\frac{(\tau_1-\tau_2)^2 + (\tau_2-\tau_3)^2 + (\tau_3-\tau_1)^2}{2}}=S_y \tag{11}$$

フォンミーゼス応力について得られた結果と同様に、八面体応力に基づく基準が定義されます。その結果、八面体応力が単純応力降伏限界よりも大きければ、降伏が起こると予想されます。

フォンミーゼス応力は、例えば、炭化水素貯留層の掘削など、配管が高圧かつ複合的な荷重条件下に置かれることが予想される分野で適用できます。この場合、フォンミーゼス応力の公式は$^5$ のように書くことができます:

$$ \sqrt{\frac{(\tau_z-\tau_t)^2 + (\tau_t-\tau_r)^2 + (\tau_r-\tau_z)^2}{2}}=\tau_v \tag{12}$$

ここで、$z$ 、$r$ 、$t$ は軸方向応力、半径方向応力、接線方向応力です。つまり、上式から得られるフォンミーゼス応力が材料の単純引張降伏応力以上であれば、降伏が起こると考えられます。

トレスカ降伏基準

トレスカ降伏基準は、降伏前の材料の最大応力を決定するために使用される一般的な基準のもう一つの例です。トレスカの降伏基準で降伏を計算すると、フォンミーゼス法に比べて常に低い結果が得られます。科学界では、より保守的な破壊の推定値として一般的に知られています。また、最大せん断応力降伏基準$^4$ としても知られています。

最大せん断応力の最も一般的な式は次のとおりです:

$$ [(\tau_1-\tau_2)^2-(S_y)^2][(\tau_2-\tau_3)^2-(S_y)^2][(\tau_3-\tau_1)^2-(S_y)^2]=0 \tag{13}$$

応力成分の大きさの順序を知ることは、この基準を単純化するのに役立ちます。上の式は次のようになります:

$$ (\tau_1-\tau_3)^2-(S_y)^2=0 \tag{14}$$

トレスカ降伏基準は線形ですが、フォンミーゼス降伏基準は非線形です。しかし、トレスカ降伏曲面には特異点が含まれることがあります。2つの条件間の予測値の差は比較的小さくなります。

参考

Hooke, R., “Lectures de potentia restitutiva or of spring explaining the power of springing bodies”, 1678
Capecchi, D., Ruta, G., “Strength of Materials and Theory of Elasticity in 19th Century Italy”, 2015
Bourgoyne Jr, A. T., Millheim, K. K., Chenevert, M. E., Young Jr, F. S., “Applied Drilling Engineering”, 1986
Armenàkas, A. E., “Advanced Mechanics of Materials and Applied Elasticity”, 2006
Shigley, J. E., Mischke, C. R., Budynas, R. G., “Mechanical Engineering Design”

2024年3月13日