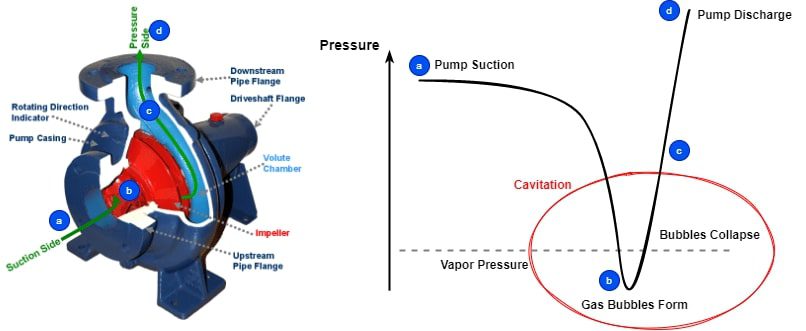
キャビテーションは、局所的な静圧が作動液の蒸気圧を下回ると発生し、液体が蒸発して蒸気泡になります。これらの気泡は小さなポケットに閉じ込められ、下流に移動します。局所圧力が再び上昇すると、これらの蒸気ポケットは破裂し、局所的な衝撃波を引き起こし、ポンプ装置を損傷させ、過度の騒音や振動につながります。

図1: キャビテーションによる羽根の深刻な損傷(^1)
簡単に言うと、キャビテーションとは、ポンプ内で蒸気気泡が急速に形成され、崩壊することによって引き起こされる有害な現象です。キャビテーションを発見し、軽減するために使用される方法を深く掘り下げる前に、まずキャビテーションの原因を理解しましょう。
キャビテーションの原因
相変化と平衡の物理学
キャビテーションは相転移と平衡の物理学によって支配されています。この記事では水について述べますが、同じ原理は他の純粋な物質にも拡張することができます。
水の沸点は373Kであり、これは373Kで大気圧の場合、水には液体と蒸気の平衡状態が存在することを意味します。実際、圧力が変化するにつれて、このような平衡が存在する連続的な温度範囲を見つけることができます。この相平衡は、図2に示すように、圧力-温度(P-T)図上に可視化されます。表面をP-T平面に投影すると、図3に示すようなP-T線図が得られます。
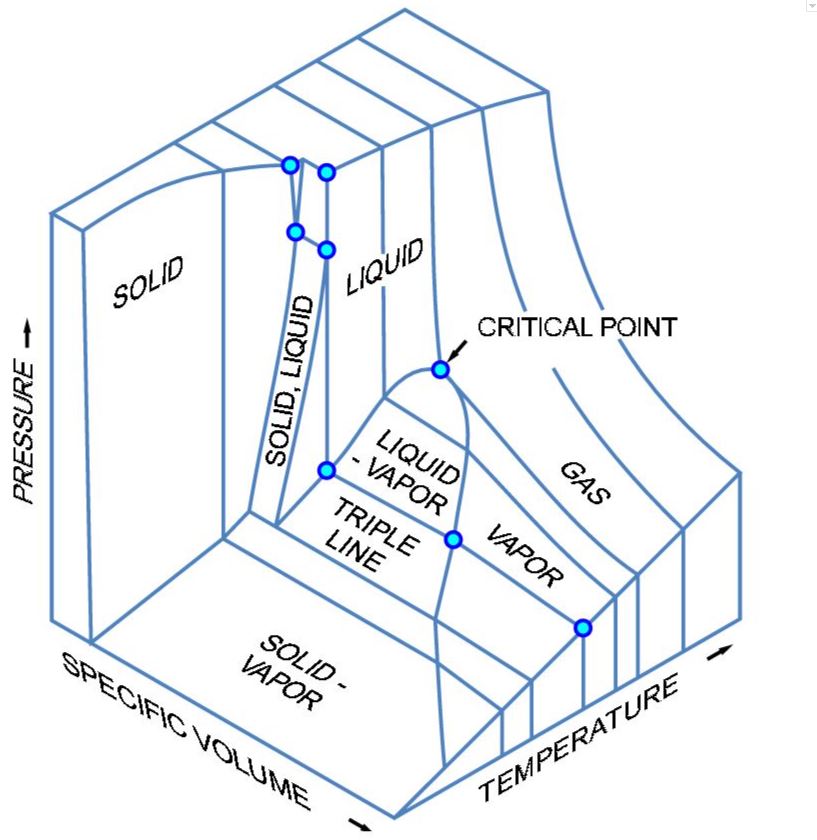
図2: 水の3次元相図(^8)
相変化とキャビテーション
ポンプ入口の上流では、摩擦損失と加速度により流れの静圧が低下します。流体が下流に流れると、ブレードの厚さと入射角により圧力はさらに低下します。
このプロセスは等温、すなわち流体の温度は変化しません。図3では、プロセスは、BとCの間の液体領域から出発して、上から下に垂線をたどります。終点が液体-蒸気ラインを横切るほど圧力が低下すると、キャビテーションが発生します。
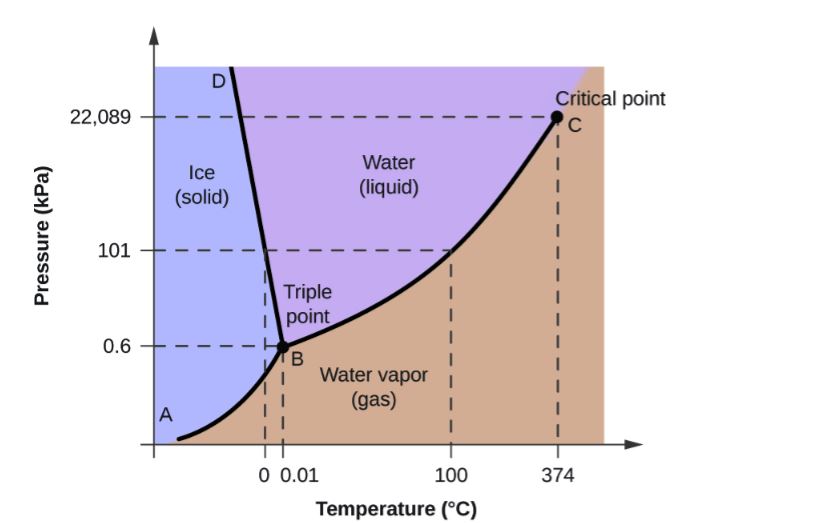
図3: 水のP-T相図(^6)
キャビテーションと正味吸込ヘッド
キャビテーションは通常、有効吸込みヘッド(Net Positive Suction Head Available)\(NPSH_a\) 、およびポンプがキャビテーションのない状態で運転するための必要吸込みヘッド(Net Positive Suction Head Required)\(NPSH_r\) 。\(NPSH_a\) は次のように定義されます:
$$NPSH_a = \frac{p_s – p_v}{\rho g} + \frac{C_s^2}{2g}\tag{1}$$
記号 |
意味 |
| \(p_s\) | ポンプ吸込口の静圧 |
| \(p_v\) | 所定の温度での液体蒸気圧 |
| \(\rho\) | ポンプ入口での流速 |
| \(g\) | 重力加速度 |
| \(C_s\) | 流体密度 |
しかし、キャビテーションが始まる圧力の正確な値を予測することは困難であり、多くの要因に依存します。ポンプ揚程が3%低下する正味吸込みヘッド((NPSH_3))は測定が非常に容易であり、キャビテーションを回避するために推奨される最小(NSPH)を示すポンプ仕様で最も一般的に使用される用語です。
キャビテーションはなぜ悪いのか?
キャビテーションの主な影響の1つは、ポンプ性能の低下です。図5、6、7に示すように、流れ中のキャビテーション率が増加すると、ポンプが発生させるヘッドは減少します。
キャビテーションはまた、キャビテーション気泡の爆縮から発生する高圧パルスにより、さらなる騒音と振動を引き起こします。これらの爆縮は、kHz帯の広帯域高周波流体媒介ノイズの原因となります。
キャビテーションはまた、図9~図12に示すような構造的損傷を引き起こす可能性があります。
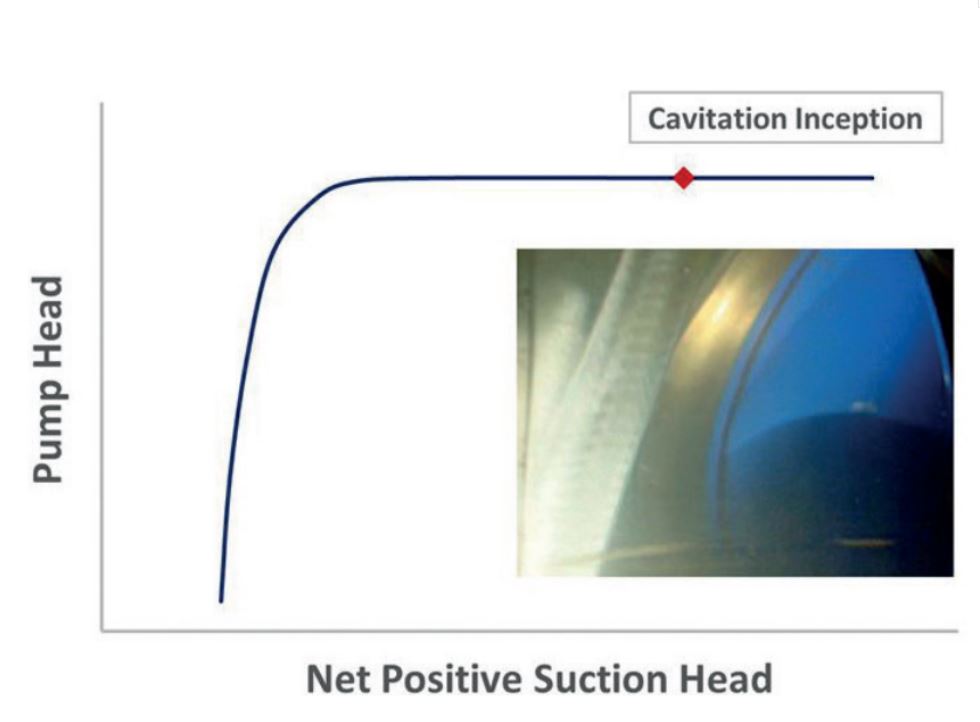
図5: キャビテーションの発生、発生したヘッドに顕著な低下は見られない(^2)
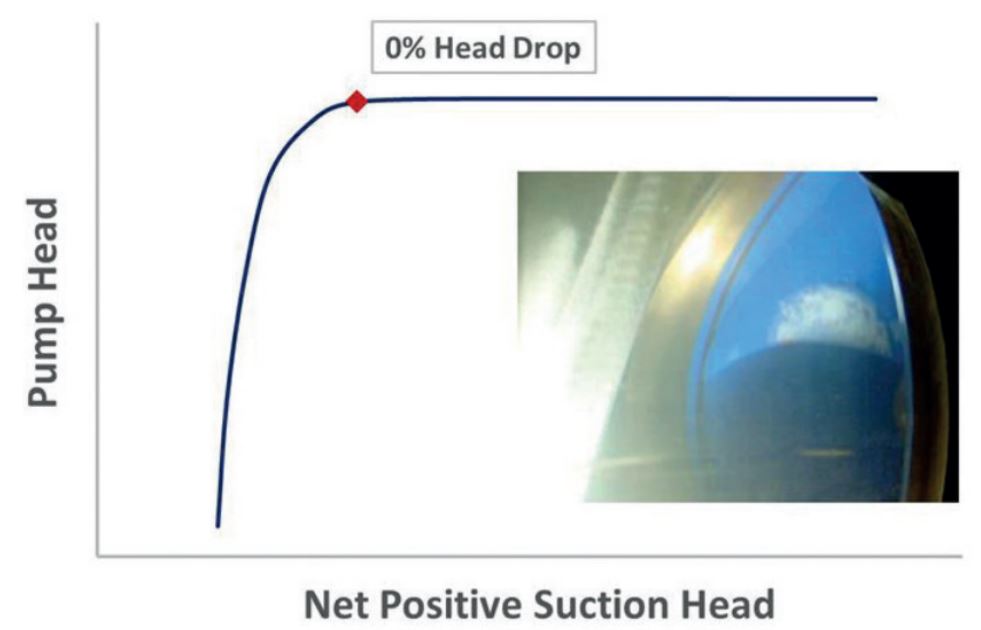
図6: 中程度のキャビテーション、ポンプヘッドの低下が始まる(^2)

図7: ヘッドの3%低下に対応するキャビテーション(^2)
異なる質量流量に対するヘッドの降下チャートを図 8 に示します。ここでは、流量と発生ヘッドの両方が、設計点発生ヘッドと設計点質量流量を用いて正規化されています。キャビテーション開始\(\sigma_i\) 、ヘッド降下開始\(\sigma_o\) 、1%ヘッドドロップ\(\sigma_1\) 、および 3%ヘッドドロップ\(\sigma_3\) を示す曲線が追加されています。ここで、\(\sigma_x\) は以下のように定義されています:
$$\sigma_x = \frac{2g NPSH_x}{u_{1a}^2} \tag{2}$$
記号 |
意味 |
| \(NPSH_x\) | 正味吸込ヘッド |
| \(g\) | 重力加速度 |
| \(u_{1a}\) | シュラウドでの入口ブレード速度 |
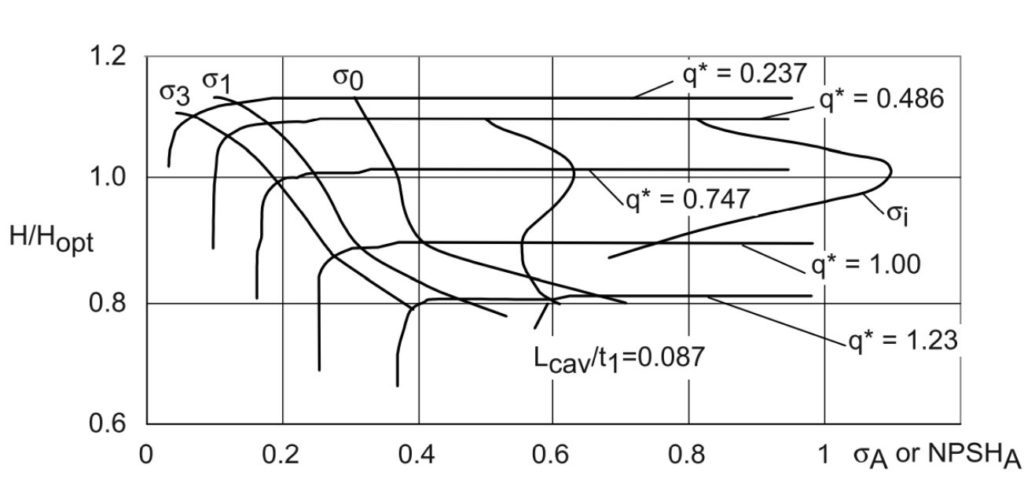
図 8: 異なる質量流量に対するヘッドドロップ曲線(^7)

図9: キャビテーションによるシュラウドインペラの侵食

図 10: インペラのキャビテーション損傷(^4)

図 11: キャビテーションによるインペラの損傷(^5)

図12: ディフューザブレードのキャビテーション侵食(^7)
キャビテーションが発生する場所
キャビテーションは非常に一般的な現象であり、不適切な入口圧力または不適切な設計の部品で作動するポンプ内で発生する可能性があります。遠心ポンプまたは混合流ポンプの場合、キャビテーションは通常、インペラまたはインデューサの入口で発生します。軸流ポンプの場合、キャビテーションは、図13に示すように、シュラウドに近いブレード先端の入口付近、またはブレード吸込側の中央でも発生することがあります。
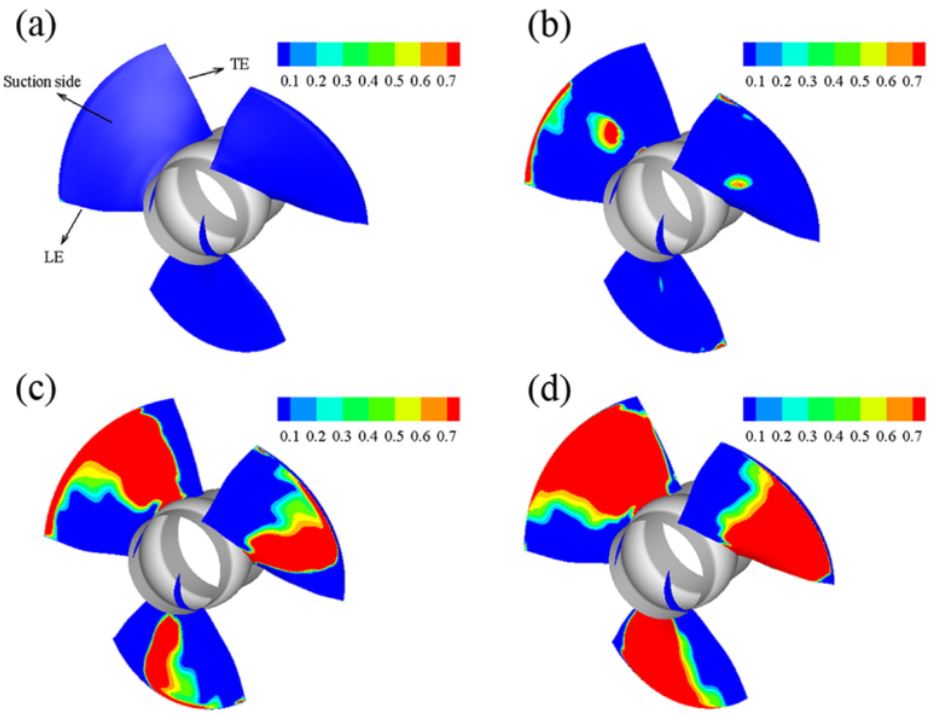
図 13: 入口圧力の異なる軸流インペラの蒸気分率で示されるキャビテーション領域。結果は(SST)k-ω乱流モデルおよび二相流(^3) を使用して得られています。
キャビテーションを回避するには?
キャビテーションを回避する方法は、キャビテーションの種類、場所、強度によって異なります。キャビテーションの損傷パターンやキャビテーションの位置に基づいて提案された原因および対処法の一部は、次のとおりです。\(^7\) :
キャビテーションパターンの位置/特徴 |
原因 |
解決策 |
| リーディングエッジに近い吸込側に観察されるキャビティや損傷の付着。 | 入射角が大きすぎる、不利な前縁プロファイル。 | 流れの角度とブレードの角度の間にミスマッチがあるため、流量を増やすか、流れにプレローテーションを導入するか、インレットリングを使用して軸流速度を上げるとキャビテーションが減少します。 |
| 吸込側で渦の剥離を伴う長く厚いキャビティ。前縁から遠く離れたインペラチャンネル内の吸込側で観察される損傷。 | 吸込揚程が低すぎる、入射角が大きすぎる。 | 流量を増やして流速を上げるか、ブレードに穴を開けて吸込側から圧力側へ流れるようにします。 |
| 圧力側の空洞の付着、シュラウドに近いリーディングエッジ付近の損傷。 | 前縁の形状が悪い、流量が過大。 | 流量を減らし、ブレードを削り、圧力面のプロフィールを改善。 |
| 流れの再循環によるインペラチャンネル内のキャビティクラウド。 | インペラの直径が大きい、流量が少ない、ブレードの角 度が高い(ブレードの角度が高いほど、ブレードが メリオディナルであることを意味する)ために、流れが 激しく減速している場合。 | 流量の増加、研磨による前縁形状の改善。 |
| 非シュラウド羽根車におけるギャップキャビテーション。 | 高いブレード負荷。 | 圧力面におけるブレードエッジの丸み。 |
キャビテーション低減の一般原則とその効果
上記の解決策に加えて、キャビテーションに関連するあらゆる損傷は、以下の方法の1つまたは複数を使用することで軽減することができます:
- 吸入圧を高めることは常に最良の解決策です。十分な入口圧力はキャビテーションを減少させ、あるいはなくすことができますが、常にそうできるとは限りません。
- インレット圧を上げることが不可能な高速用途では、代わりにインデューサーが使用されます。インデューサはある程度のキャビテーションを処理することができ、通常、流れがインペラ入口に到達するまでにキャビテーション気泡は抑制され、入口圧力はメインインペラ内で大きなキャビテーションが発生しないように十分に上昇します。
- ロケットのターボポンプで想定されるような超高速大量臨界用途には、高強度ニッケルクロム鋼やチタン、インコネルなど、よりキャビテーションに強い材料を使用します\(^7\) 。

図 14: 前縁に近いブレード吸込側の付着空洞(^7)

図 15: ブレードによって切断された渦ロープ。キャビテーション容積が大きいため、材料損傷の可能性が大きい(^7)
キャビテーションの予測方法
一般的に、解析技術を使用してキャビテーションを予測することは非常に困難です。実験を用いてキャビテーションをチェックする方がはるかに簡単です。しかし、通常、実験には費用と時間がかかります。さらに、ポンプが運転された後に性能の問題をトラブルシューティングするのではなく、キャビテーションを防止するようにポンプが設計されていれば、ポンプのお客様にとって有益です。
CFDシミュレーションは、キャビテーションを最小限に抑えたポンプシステムを開発するための設計空間の探索を可能にすることで、貴重な洞察を加えることができます。
キャビテーションを最小化するポンプインレットの設計
ここでは、ポンプ流入側の圧力がキャビテーションを防止するのに十分かどうかを評価するために使用できる、ポンプの半経験的解析的計算方法(\(NPSH\) )について説明します。ここで紹介する関係はGülich\(^7\) のもので、遠心ポンプだけでなく混合流ポンプにもある程度有効です。キャビテーションは局所的な圧力極小領域で発生し、この極小領域はブレード前縁付近の局所的な過剰流速によって形成されます。式3は、これらの効果を捉えるために使用することができます:
$$NPSH_3 = \lambda_c\frac{c_{1m}^2}{2 g} + \lambda_w\frac{w_1^2}{2 g}\tag{3}$$
記号 |
意味 |
| \(\lambda_c\) | 入口での流れの加速と損失を考慮した係数。 |
| \(\lambda_w\) | 翼入口での低圧ピークを示す係数 |
| \(w_1\) | 羽根車入口におけるシュラウドでの相対流速。 |
| \(c_{1m}\) | 羽根車入口絶対流速の子午面成分。 |
| \(g\) | 重力加速度 |
\(\lambda_c\) の値は、軸方向流入口では~1.1、半径方向流入ケーシングでは1.2~1.35とすることができます。ポンプでは通常、絶対流速は相対流速よりもはるかに小さいため、\(\lambda_w\) の値ははるかに重要です。\(\lambda_w\) の値は、入口流速プロファイル、インペラ、コレクタ、シール設計を含む他の多くのパラメータに依存します。おおよそ、\(\lambda_w\) の値は、設計流量に近い運転をしているポンプの第一近似値として、インペラの場合は0.1から0.3の間、インデューサの場合は0.03から0.06の間と考えることができます。\(\lambda_c\) と\(\lambda_w\) が吸込口径に依存しないと仮定した場合、特に\(\lambda_w\) については厳密には正確ではありませんが、\(NPSH_3\) が最大となる最適化された吸込口径を以下の式を用いて求めることができます:
$$c_{1m} = \frac{4Q}{\pi(d_1^2 – d_n^2)}\tag{4}$$
$$w_1^2 = c_{1m}^2+\left(u_{1a}-\frac{c_{1m}}{\tan{\alpha_1}}\right)^2\tag{5}$$
$$ u_{1a} = \frac{\pi d_1 n}{60}\tag{6}$$
記号 |
意味 |
| \(c_{1m}\) | インペラ翼入口での絶対流速の子午面成分 |
| \(Q\) | 体積流量 |
| \(n\) | ブレード回転速度(rpm |
| \(\alpha_1\) | シュラウドでの周方向流速と絶対流速のなす角度 |
| \(w_1\) | 羽根車入口相対流速 |
| \(u_{1a}\) | シュラウドでのインペラ入口ブレード速度 |
| \(d_1\) | インペラ/インデューサ入口直径 |
| \(d_n\) | インペラ/インデューサハブ直径 |
式4~6を式3に代入して\(NPSH_3\) 、\(d_1\) に関して微分して0と等しくすると、以下の結果が得られます。この式はまた、\(d_n\) が\(d_1\) から独立していると仮定しています。\(d_n\) は材料の機械的特性によって決まるため、通常はこのようになります。
$$ d_1 = \left(d_n^2 +\frac{1.48}{1000} \psi n_q^{\frac{3}{4}} d_2^2 \left(\frac{\lambda_c + \lambda_w}{\lambda_w} \right )^{\frac{1}{3}}\right)^{\frac{1}{2}} \tag{7}$$
$$ \psi = \frac{2gH}{u_2^2} \tag{8}$$
$$n_q = n\frac{\sqrt{\frac{Q_opt}{f_q}}}{H^{0.75}} \tag{9}$$
記号 |
意味 |
| \(d_2\) | 羽根車出口直径 |
| \(w_1\) | 羽根車入口相対流速 |
| \(\psi\) | ヘッド係数。式 8 で定義。 |
| \(n_q\) | 比流速で、式9のように定義されます。 |
| \(H\) | ポンプで発生する揚程 |
| \(f_q\) | ポンプ入口のエントリー数 |
係数\(\lambda_w\) は式10に示される式を使用して計算することもできますが、この式は設計流量に近い運転条件と入口翼角\((10^0\) から\(45^0\) の間で再び成立します。
$$\lambda_w = 0.3\left(\tan{\beta_{1a}}\right)^{0.57} \tag{10}$$
記号 |
意味 |
| \(\beta_{1a}\) | インペラ/インデューサシュラウドでの相対流角度 |
式10は、\(\lambda_c\) = 1.1である完全な軸方向インレットケーシングと、\(\lambda_c\) = 1.35である半径方向インレットケーシングを用いた実験結果のカーブフィッティングによるものです。さらに、実験結果とカーブ生成結果の間には25%の標準偏差があります。
異なる流量に対するキャビテーション回避のための最小入口圧力
通常、解析的な方法を用いて異なる流量における所定のポンプの\(NPSH_3\) を計算することは困難ですが、Gülich\(^7\) は第一近似として使用できる方法を提供しています。この方法は、流れの入射角が正で、流れがインペラのスロートで下流に向かって減速している間は、\(NPSH_3\) が比較的平坦であるという観察に基づいています。しかし、流れの入射角が負になり、流体がインペラのスロートまで加速し始めると、\(NPSH_3\) は急激に増加します。さらに、ディフューザの存在も、\(NPSH_3\) の早期上昇の原因となります。
最大流量は次のように計算できます:
$$Q_{SF} =\frac{f_q A_1 \tan\beta_{1\beta} u_{1a}}{\tau_1\left(1+\frac{\tan\beta_{1B}}{\tau_1\tan\alpha_1} \right )} \tag{11}$$
記号 |
意味 |
| \(f_q\) | ポンプ入口エントリー数 |
| \(A_1\) | インペラ入口面積 |
| \(\beta_{1b}\) | シュラウドでのインペラ入口ブレード角度 |
| \(u_{1a}\) | シュラウドでのインペラ入口ブレード速度 |
| \(\tau_1\) | インペラ入口ブレード閉塞係数 |
| \(\alpha_1\) | 円周方向と絶対速度の角度 |
インペラのスロートで流体の減速が停止する流量は次のように計算されます:
$$ Q_W = \frac{f_q A_1 u_{1m}}{\sqrt{\left(\frac{A_1}{Z_{La}A_q} \right )^2 – 1}+\frac{1}{\tan\alpha_1}}\tag{12}$$
記号 |
意味 |
| \(Z_{la}\) | ポンプ入口羽根枚数 |
| \(u_1m\) | 平均インペラ入口ブレード速度 |
| \(A_{1q}\) | 各ブレードペアのインペラ入口スロート面積 |
| \(f_q\) | ポンプインレットのエントリ数 |
| \(A_1\) | インペラ入口面積 |
| \(\alpha_1\) | 円周方向と絶対速度の角度 |
インペラ出口の絶対流速がディフューザスロートの流速と等しくなる流量は、次のように計算できます:
$$Q_C =\frac{f_q A_2 u_2 \gamma}{\frac{f_q A_2 }{Z_{Le}A_{3q}} + \frac{\tau_2}{\eta_v \tan\beta_{2B}}} \tag{13}$$
記号 |
意味 |
| \(Z_{Le}\) | ディフューザ入口のブレード数 |
| \(A_{3q}\) | 各ブレードペアのディフューザ入口スロート面積 |
| \(\eta_v\) | 容積効率 |
| \(\tau_2\) | インペラ出口ブレード閉塞率 |
| \(A_2\) | インペラ出口面積 |
| \(f_q\) | ポンプインレットのエントリー数 |
| \(\beta_{2b}\) | インペラ出口のブレード角度 |
| \(\gamma\) | インペラ出口のスリップ係数 |
ここで、式11~13を用いて計算した上記の3つの流量を用いて、異なる流量に対する\(NPSH_3\) :
ショックレス流量\(Q_SF\) と非減速インペラのスロート流量\(Q_W\) の平均値に近い流量で圧力面上にキャビテーションが発生すると仮定できます。
$$ Q_{PS} = \frac{1}{2}\left(Q_{SF} + Q_W\right) \tag{14}$$
ディフューザは、\(Q_C\) <\(Q_PS\) の場合にキャビテーションの発生に影響を与えると考えられ、その場合、\(Q\)>\(Q_c\) の後に\(NPSH_3\) が急激に上昇することが予想されます。そうでない場合は、\(Q\)>\(Q_PS\) で\(NPSH_3\) の急激な上昇が見られます。ここで、\(NPSH_3\) が比較的平坦な領域については、\(\lambda_w\) は式 10 を使って計算できます。\(\lambda_w\) と\(NPSH_3\) は式 3 を使って計算できます。\(NPSH_3\) が急激に増加する流量については、以下の式を使用できます:
$$ NPSH_3 = NPSH_{3SA} \left(\frac{Q}{Q_{SA}}\right)^x \tag{14}$$
$$ Q_SA = min\left(Q_{PS},Q_C\right) \tag{15}$$
ここで、\(NPSH_{3SA}\) は、\(NPSH_3\) が急激に増加し始める流量に対応する、3%のヘッドドロップが観察される正味正吸込揚程、\(Q_SA\) は、\(NPSH_3\) が急激に増加し始める流量、x は、2 から 3 の間の任意の値を持つ指数です。
ポンプのキャビテーションを評価する実験方法
キャビテーションは、インペラの上流で圧力変換器を使用することによって簡単に測定できる、広範なスペクトルの流体媒介ノイズをもたらします。このような実験の実用的な用途としては、キャビテーションの発生を特定したり、キャビテーションによる浸食の程度を予測したりすることが挙げられます。遠心ポンプの場合、キャビテーション係数は式2のように定義できます。
実験は、異なる質量流量およびポンプ入口圧力に対するノイズの実効値を記録するために実施することができます。これにより、下図に示すように、キャビテーションを介した騒音とキャビテーション係数の関係が得られます。
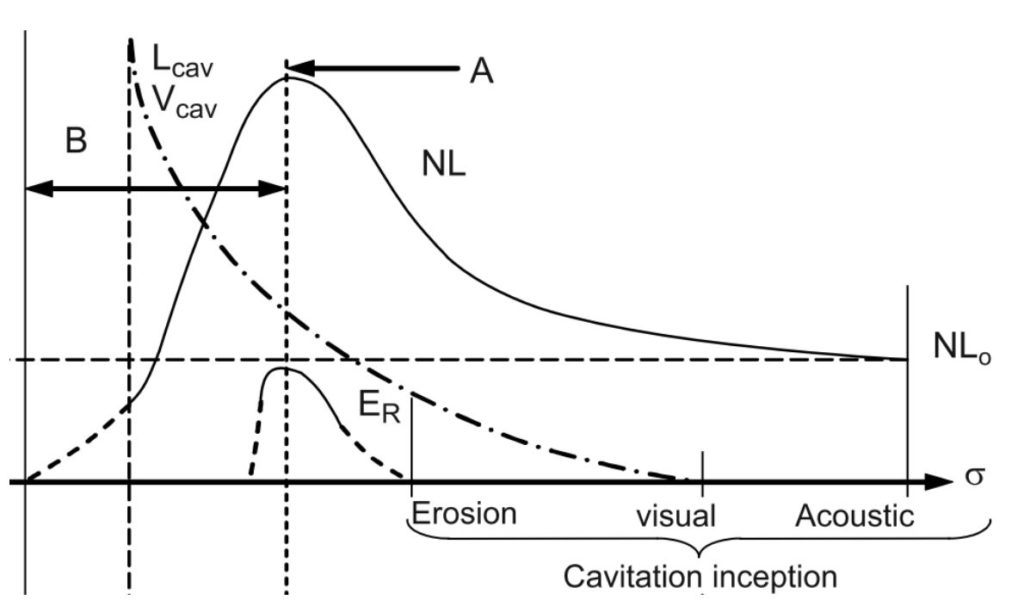
図16: キャビテーション流体騒音とキャビテーション係数の関係(^7)
上図からわかるように、キャビテーション係数または入口圧力が十分に高い場合、騒音レベルはほぼ一定であり、これはポンプ運転時のバックグラウンドノイズによるものです。通常、この騒音は流れの乱れ、非定常翼力、機械的騒音によって発生します。キャビテーション係数が低下すると、騒音レベルは上昇します。この騒音レベルの増加は、インペラ入口で形成されるキャビテーション気泡によるものです。キャビテーション気泡の体積と数が増加するにつれて騒音レベルは増加し続け、最大に達します。領域Aの左側で騒音レベルが低下するのは、複数の理由によるものです。まず、追加騒音の発生につながる爆縮のポテンシャルエネルギーは、圧力差と気泡体積の両方に依存します。キャビテーション気泡のポテンシャルエネルギーの式は以下のとおりです:
$$ E_pot = \frac{4}{3}\pi\left(R_o^3 – R_e^3\right)\left(p-p_v\right) \tag{16}$$
記号 |
意味 |
| \(R_o\) | キャビティ形成時の気泡半径 |
| \(R_e\) | 爆縮終了時の気泡半径 |
| \(p_v\) | 蒸気圧 |
| \(p\) | 気泡を取り囲む流体圧力 |
入口圧力が下がると、気泡半径は大きくなりますが、圧力差は小さくなります。これらの相反する現象により、ポテンシャルエネルギーが減少し、騒音が減少します。さらに、キャビテーション気泡のサイズと数が大きくなると、液体ほど音波の伝導性が良くない気体である気泡にある程度の騒音が吸収され、その結果、騒音レベルはバックグラウンドノイズ以下になります。さらに、領域Aでは、キャビテーション気泡の視覚的認識と背景騒音以上の騒音レベルの上昇との間にタイムラグがあることにも注意が必要です。これは、目視では検知できないほど微細な気泡が発生しているためと考えられます。
図17は、異なる回転速度における流体伝搬騒音レベルと固体伝搬騒音レベルの両方を正規化したものです。固体伝搬ノイズレベルは、インレットケーシングの外側にある加速度計を使用して測定されています。固体伝搬ノイズは、ベアリング、ギアボックス、シールなどから発生するバックグラウンドノイズから構成されており、これらのノイズも回転速度に依存するため、流体伝搬ノイズの場合のように曲線が互いに重ならないのです。
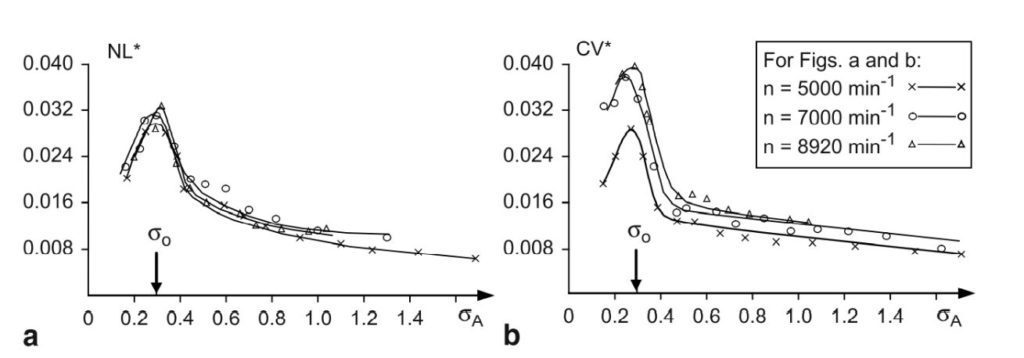
図17: 異なる回転速度における流体伝搬騒音レベルと固体伝搬騒音レベル(^7)
参考
- “Cavitation and NPSH.” KSB, 22 February 2022, https://giw.ksb.com/blog/cavitation-and-npsh. Accessed 24 October 2022
- Visser, Frank. “Cavitation in Centrifugal and Axial-Flow Pumps.” 2022.
- Feng, Weimin. “Simulation of cavitation performance of an axial flow pump with inlet guide vanes.” Advances in Mechanical Engineering, vol. 8, no. 6, June 2, 2016, https://doi.org/10.1177/1687814016651583.
- “How to Avoid Pump Cavitation? 6 Main Steps.” Linquip, 22 August 2021, https://www.linquip.com/blog/what-is-pump-cavitation/. Accessed 24 October 2022.
- Nickerson, Philip. “Cavitation, the ‘pump disease’ – Responsible Seafood Advocate.” Global Seafood Alliance, 1 May 2007, https://www.globalseafood.org/advocate/cavitation-the-pump-disease/. Accessed 24 October 2022.
- “Phase Diagrams | Chemistry for Majors.” Lumen Learning, https://courses.lumenlearning.com/chemistryformajors/chapter/phase-diagrams-2/. Accessed 14 October 2022.
- Gülich, Johann Friedrich. Centrifugal Pumps. Springer Berlin Heidelberg, 2010. Accessed 7 October 2022.
- “File:PVT 3D diagram-en.svg.” Wikimedia Commons, https://commons.wikimedia.org/wiki/File:PVT_3D_diagram-en.svg. Accessed 13 October 2022.
- Singhal, A.K. et al. (2002) “Mathematical basis and validation of the full cavitation model,” Journal of Fluids Engineering, 124(3), pp. 617–624. Available at: https://doi.org/10.1115/1.1486223.
SimScale製品紹介資料ダウンロード

SimScaleの特徴と計算事例をまとめた資料を用意しております。