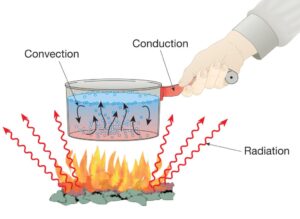
境界条件とは、CAE(シミュレーション技術)で解析対象の挙動を決めるために設定する条件のことです。境界値問題との関係や基本的な考え方をやさしく解説します。
境界値問題とは、境界上の一連の条件がわかっている領域で解かれる微分方程式(または微分方程式系)のことです。区間の一方の極端な条件だけがわかっている「初期値問題」とは対照的です。
境界値問題は、構造解析から流体解析、熱解析、電磁界解析に至るまで、膨大な量の現象と応用をモデル化するため、非常に重要です。初期値問題は通常、時間的に解かれる問題を指しますが、境界値問題は空間的に解かれる微分方程式に基づくすべての問題で自然に生じます。
\(^1\)境界値問題は、Jacques Charles François Sturm (1803-1855) とJoseph Liouville (1809-1882) によって広く研究されてきました。彼らは、微分問題の解の存在と一意性を保証する条件と、それが境界条件によってどのように影響されるかを研究しました\(^2\) 。Sturm-Liouville理論は、問題が「よく解かれている」かどうか、また、どのようにして解を得ることができるかを理解することができるので、あらゆる計算問題にとって非常に重要です。
境界条件の種類
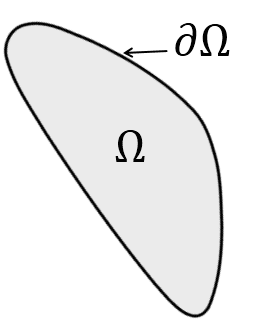
常微分方程式も偏微分方程式も境界条件を解く必要があります。領域の境界にはさまざまな種類の境界条件を課すことができます(図1)。境界条件の選択は、計算問題の解決にとって基本的なものです。B.C.の課し方を誤ると、解が発散したり、誤った解に収束したりする可能性があります。
境界条件には5つのタイプがあります:
- ディリクレ境界条件(タイプIとも呼ばれます)
- ノイマン境界条件(タイプIIとも呼ばれます)
- ロビン境界条件(タイプIIIとも呼ばれます)
- 混合境界条件
- コーシー境界条件
ディリクレ境界条件
ディリクレ境界条件は、Peter Gustav Lejeune Dirichlet (1805-1859, 図2)\(^3\) にちなんで命名された境界条件の一種です。

この条件は、領域の境界に沿って未知関数が取るべき値を指定します。例えばラプラス方程式を考えると、ディリクレ境界条件を用いた境界値問題は次のように書けます:
$$ \Delta \varphi (\underline{x}) = 0 \qquad \forall \underline{x}\in \Omega \tag{1}$$
$$ \varphi (\underline{x}) = f(\underline{x}) \qquad \forall \underline{x}\in \partial \Omega \tag{2}$$
ここで,\(\varphi\) は未知関数、\(\underline{x}\) は独立変数(空間座標など)、\(\Omega\) は関数領域、\(\partial\Omega\) は領域の境界、\(f\) は\(\partial\Omega\) 上で定義されるスカラー関数です。数値シミュレーションの枠組みでは、通常、解かれる代数系に直接課されます。数値アルゴリズムから導かれる次のような代数系を考えてみましょう:
$$ \begin{bmatrix} k_{1,1} & k_{1,2} & . & k_{1,m-1} & k_{1,m}\\ k_{2,1} & k_{2,2} & . & k_{2,m-1} & k_{2,m}\\ . & . & . & . & . \\ k_{m-1,1} & k_{m-1,2} & . & k_{m-1,m-1} & k_{m-1,m}\\ k_{m,1} & k_{m,2} & . & k_{m,m-1} & k_{m,m} \end{bmatrix} \begin{bmatrix} x_1\\ x_2\\ .\\ x_{n-1}\\ x_n \end{bmatrix} = \begin{bmatrix} a_1\\ a_2\\ .\\ a_{m-1}\\ a_m \end{bmatrix} $$
ここで、\(k_{ij}\) は代数演算子(剛性行列など)の要素、\(x_i\) は未知数(つまり問題の自由度)、\(a_i\) は既知の項です。\(n^{th}\) の自由度にディリクレ境界条件を課す最も簡単な方法は、次のように系を修正することです:
$$ \begin{bmatrix}
k_{1,1} & . & . & . & k_{1,m}\\ . & . & . & . & .\\ 0 & 0 & 1 & 0 & 0 \\ . & . & . & . & . \\ k_{m,1} & . & . & . & k_{m,m} \end{bmatrix} \begin{bmatrix} x_1\\ .\\ x_n\\ .\\ x_m \end{bmatrix} = \begin{bmatrix} a_1\\ .\\ f\\ .\\ a_m \end{bmatrix} $$
ここで\(f\) は\(n^{th}\) の自由度が取るべき値です。
ノイマン境界条件
ノイマン境界条件は、Carl Neumann (1832 - 1925, Figure 3)\(^3\) にちなんで命名された境界条件の一種です。常微分方程式(ODE)または偏微分方程式(PDE)に課されるとき、解の微分が領域の境界で取る値を指定します。例えば、ラプラス方程式を考えると、ノイマン境界条件による境界値問題は次のように書けます。
$$ \Delta \varphi (\underline{x}) = 0 \qquad \forall \underline{x}\in \Omega \tag{3}$$
$$ \frac{\partial \varphi (\underline{x}) }{\partial n}=f(\underline{x}) \qquad \forall \underline{x}\in \partial \Omega \tag{4}$$
ここで、\(n\) は境界面への単位法線です。\(\Omega\subset R^3\).

常微分方程式 (すなわち\(\Omega\subset R^1\)) の場合、境界に垂直な導関数は大域導関数\(\varphi’\) と一致します。時間依存性を(通常の有限差分ではなく)有限要素法で解く場合、このタイプの境界条件が最も一般的です。ノイマン境界条件は、どのような有限要素法においても、弱定式化の展開に自然に現れるため、「自然境界条件」とも呼ばれます。次のような簡単な方程式を考えてみましょう:
$$ -u”(x)=p(x) \qquad \forall x \in \mathbb{R} \tag{5}$$
\(u\) は未知のスカラー場、\(p\) は与えられたスカラー関数です。この方程式は、例えば1次元の熱拡散や梁の引張/圧縮など、多くの現象を支配しています。有限要素法では、この方程式を微分(強)形式から積分(弱)形式に書き換えます。この変換には2つのステップがあります:
1.積分:
$$ -\int_a^bu”(x)\nu (x)\: dx=\int_a^bp(x)\nu (x)\: dx \tag{6}$$
\(\nu(x)\) は形状関数。
2.グリーンの定理を適用して、導関数の分布を一様にする。
$$ \int_a^bu'(x)\nu'(x)\: dx=\int_a^bp(x)\nu (x)\: dx + [u'(x)\nu (x)]_a^b \tag{7}$$
このように、境界上の未知場の微分を含む項が自然に現れます。
- 1次元問題の場合,この項は区間の両端を指します.
- 2次元問題では、領域の輪郭を指します。
- 3次元問題では境界面を指します。
右辺に境界項があることで、ノイマン境界条件の2つの特性が強調されます:
- 同次ノイマン境界条件は明示的な条件付けなしに自然に満たされます。
- ディリクレ境界条件は通常、右辺の項を修正することで適用されるので、ディリクレ境界条件が課されるすべての境界で同次ノイマン条件が適用されます。
ロビン境界条件
ロビン境界条件は,Victor Gustave Robin (1855-1897)\(^4\) にちなんで命名された境界条件の一種です.これは境界上の場の値とその導関数の線形結合で構成されます。
例えば、ラプラス方程式を考えると、ロビン境界条件による境界値問題は次のように書けます。
$$ \Delta \varphi (\underline{x}) = 0 \qquad \forall \underline{x}\in \Omega \tag{8}$$
$$ a \varphi (\underline{x}) + b\frac{\partial\varphi(\underline{x})}{\partial n} = f(\underline{x}) \qquad \forall \underline{x}\in \partial \Omega \tag{9}$$
\(a\) と\(b\) は実数パラメータです。この条件は「インピーダンス条件」とも呼ばれます。
混合境界条件
混合境界条件は、領域の異なる部分に異なるタイプの境界条件を適用することです。重要なことは、境界条件は境界全体に適用されなければならないということです。
混合境界条件がロビン条件と異なるのは、後者が境界の同じ領域に異なるタイプの境界条件を適用するのに対し、混合条件は境界の異なる部分に異なるタイプの境界条件を適用することを意味するからです。
コーシー境界条件
コーシー境界条件は,未知の場とその導関数\(^5\) の両方に対する条件です.コーシー条件は2つの制約(ディリクレ境界条件とノイマン境界条件)を意味するのに対し、ロビン条件は未知関数とその導関数の線形結合に対する1つの制約のみを意味するので、ロビン条件とは異なります。
境界条件の応用
構造力学と固体力学
ディリクレ境界条件
固体力学は通常、変位ベースのモデルでモデル化されます。したがって、ディリクレ境界条件は、通常、与えられた点における構造の変位を課すことで構成されます。
構造力学は、相対回転を含む定式化に基づいていることが多く、計算するには有限要素近似における非線形形状関数が必要です。例えば、フレーム構造は梁理論に基づいており、関連する有限要素は6自由度(3次元空間で3つの変位+3つの回転)を持っています。
2D問題の場合、境界の各節点は、ディリクレ境界条件を適用できる3自由度を持ちます: 2つの変位(\(u_x\) と\(u_y\))と1つの回転(\(\omega\))。これらの制約は通常、次のように描かれます:

\(u_x = 0\)
\(u_y = 0\)
\(\omega = 0\)
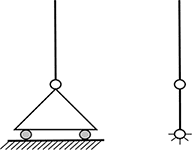
\(u_x = 0\)

\(u_y = 0\)

\(u_y =0\)
\(\omega = 0\)

\(\omega = 0\)
上の表では、地面に対する外部拘束(つまり値をゼロにする)が報告されていますが、記号はゼロとは異なる固定変位/回転を表現するためにも使用されます。
ノイマン境界条件
固体力学では、変位の空間微分はひずみテンソルに関係します。弾性では、ひずみは応力に比例するので、ノイマン境界条件はひずみと応力の両方に適用されます。
応力はコーシーの応力原理によって外力にもリンクされるため、ノイマン条件は外的荷重の適用にも使用されます。ノイマン境界条件のセクションで述べたように、均質条件は自然に満たされるため、「自由」境界は明示的にモデル化されません。
ロビン境界条件
ロビンの境界条件は、構造物の機械的インピーダンス、すなわち、調和荷重を受けたときにどれだけ運動に抵抗するかをモデル化するために使用されます。
流体力学
ディリクレ境界条件
計算流体力学 (CFD) では、古典的なディリクレ境界条件は、ある節点がとるべき速度や圧力の値から構成されます。次のような用語で境界条件を呼ぶのが一般的です。
- スリップ
境界条件: 境界に垂直な速度はゼロに設定され、境界に平行な速度は自由に設定されます。 - 滑りなし境界条件:
境界に垂直な速度と境界に平行な速度の両方がゼロに設定されます。
圧力に関する少なくとも1つの均質な境界条件(\(p=0\)など)が、開いた領域の基準として課されなければなりません。
ノイマン境界条件
速度または圧力場の微分に対する制約は、主に2つのケースで使用されます。最初のケースは対称面の適用です:
$$ \cfrac{\partial u}{\partial n} = 0 \tag{10}$$
この条件は常にディリクレ境界条件に加えて適用されるため、自然に満たされます。もう1つは、壁面摩擦がひずみ速度に比例する場合のモデル化です:
$$ S=(\nabla u + \nabla^T u) \tag{11}$$
ロビン境界条件
波を部分的に吸収する半反射壁を記述するために使用されます。あまり一般的な用途ではなく、圧力ベースのモデルにのみ使用できます。この境界条件は主に音響アプリケーションに使用されます。
熱力学
ディリクレ境界条件
熱力学では、ディリクレ境界条件は一定の温度に保たれた面(3次元問題)で構成されます。
ノイマン境界条件
熱力学におけるノイマン境界条件は、境界を横切る熱流束を表します。完全な絶縁体は均質な条件(自然に満たされる)を反映しますが、温められた境界と冷やされた境界はすべて境界条件を明示的に割り当てる必要があります。これは通常、電子部品(内向きの熱流束)または外部冷却スプレー/チャンネル(外向きの熱流束)の場合です。
電磁気学
マクスウェル方程式は一般的にポテンシャル定式化によって解かれます。\(A,\varphi\) \(A\) は磁気ベクトルポテンシャル、\(\varphi\) はスカラー電位です。
ある条件下では、(\(A,\varphi\))は切り離すことができ、電位はラプラス方程式を通して計算することができます:
$$ \Delta\varphi=0 \tag{12}$$
ディリクレ境界条件
\(\varphi\) のディリクレ境界条件は通常、導電性領域の境界部分に課されます。電線の場合、1つの部分の値は通常ゼロに設定され、電位の固定値は2つ目の部分に固定されます。通常、\(A\) の条件は、磁場が外部境界に接するように、つまりすべての磁力線が計算領域内にあるように制約します。
ノイマン境界条件
電磁気モデリングでは、ある仮説の下で、\(\nabla\varphi\) は電流密度です。均質なノイマン境界条件(すなわち、\(\nabla\varphi\cdot n=0\) )を課すことは、電流が境界を越えないように強制することを意味します。この条件は「絶縁境界」とも呼ばれ、完全な絶縁体の挙動を表します。
ロビン境界条件
電気回路のインピーダンスをモデル化するために使用され、電圧が印加されたときに回路が電流に対して示す反対を表します。また、電磁波のインピーダンスのモデル化にも使用されます。
参考
- https://www.encyclopediaofmath.org/index.php/Sturm-Liouville_problem
- https://www.encyclopediaofmath.org/index.php/Sturm-Liouville_theory
- Cheng, A. and D. T. Cheng (2005). Heritage and early history of the boundary element method, Engineering Analysis with Boundary Elements, 29, 268–302.
- Gustafson, K., (1998). Domain Decomposition, Operator Trigonometry, Robin Condition, Contemporary Mathematics, 218. 432–437.
- Morse, P. M. and Feshbach, H. Methods of Theoretical Physics, Part I. New York: McGraw-Hill, pp. 678-679, 1953.
境界条件と合わせて読みたい
SimScale製品紹介資料ダウンロード

資料請求
資料全体をご希望の方はこちらのフォームからお申し込みください。