応力-ひずみ曲線は、材料が荷重下でどのような挙動を示すかを定義するもので、これにより材料の強度、剛性、延性、および破壊限界を知ることができます。 例えば、ガラスのビー玉を地面に落とすとすぐに粉々に砕けますが、ゴム球は衝撃を受けると元の形状に戻ります。このようなガラスのビー玉とゴム球の材料挙動の違いは、応力ひずみ線図 (Stress-Strain Curve, SS線図)で説明することができます。
固体物体が荷重によってどのように変形するかは、その材料特性の結果です。これは通常、よくある疑問につながります
- なぜ力-変位の関係に基づいて材料特性を定義しないのですか?
- なぜ応力-ひずみの関係を用いるのでしょうか?
これは、力と変位が材料の外在的な特性であるという事実に起因しています。材料をある程度まで変形させるのに必要な力は、存在する材料の量に依存します。従って、力-変位の関係に基づいて材料を特性評価することは、一定の機械的特性を提供することができないため、現実的ではありません。
一方、応力とひずみは、力と変位に対応する本質的な材料特性です。例えば、直径10mmの棒鋼は、直径10cmの棒鋼と同じ応力を引張方向に負荷します。
連続的で変形可能な材料からなる平衡状態にある部品に外部荷重(F)が加わると、その部品は変形しようとします。そして材料は、均衡を維持するために、外部荷重と等しいが反対の内部力を発生させて、この変形に抵抗しようとします。
外力が体全体に一様に分布していると仮定すると、体の任意の断面積(A)を通る外力の一部(F)と、この外力に対抗する内力(F')が存在します。任意の断面におけるこの内力は「応力」として知られ、次式で表されます:
$$\sigma = \frac{F}{A}$$
さて、外部負荷がかかると、材料の内部は変形する傾向があります。この変形を測定し、任意の物体形状に対して正規化する必要性から、科学者は無次元ひずみを考え出しました。これは、変形していない形状に対する相対的な変形を表す量です。
元の長さLと長さの変化\(\Delta\)Lを持つ要素のひずみは次のように定義されます:
$$\epsilon=\frac{\Delta L}{L}$$
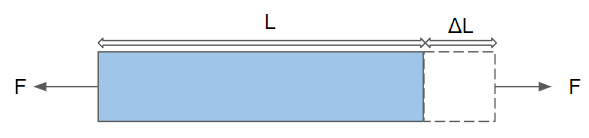
図1: 荷重を受けた試料の伸び
応力ひずみ線図の測定方法
応力ひずみ線図は通常、引張試験によって測定されます。引張試験では、試験片が破断するまで引張方向へ徐々に荷重をかけます。この試験で、測定ないし観察される特性の例は以下が挙げられます:
- 力
- 変形
- 引張強さ (極限強さ)
- 破断強度
- 試験片面積の減少
上記の測定された特性を利用することで、材料に関する以下の情報を特定することもできます:
- ヤング率
- ポアソン比
- 降伏強度
- ひずみ硬化
図3は延性材料で実施した試験の結果を示しています。これは、試験サンプルが破断に至るまでに経験する段階を強調したものです。応力-ひずみ曲線の段階に関する詳しい情報は、この記事の次のセクションで説明します。
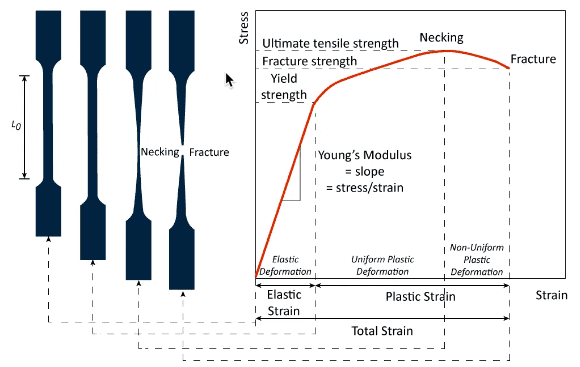
図3: 応力-ひずみ曲線の段階を経た試験サンプルの形状変化[2]
公称応力 vs 真応力 と ひずみ
応力ひずみ曲線は、引張試験中に測定される断面積の取り扱いによって 2つ の種類に分類できます。工学的には、材料の断面積は変形中も一定であると仮定され、つまり、どの荷重においても、公称応力は印加荷重を初期断面積で割ったものになります。
公称応力は、一様伸びが終了するときである最大値に達し、この値を引張強さ (Ultimate strength) と呼びます。これは上図によく示されています。その後、試験片がくびれるネッキングが始まり、ひずみが増加するにつれて公称応力は減少し、最終的に破断が起こります。
上図3に見られるように、引張試験中に試験試料が伸びるにつれて断面積は縮小します。これを考慮することで、材料の応力-ひずみ関係を正確に表すことができ、真応力と呼びます。材料の真応力を求めるには、加えられた荷重を瞬時の断面積で割る必要があります。こうすると、応力の値は引張強さを超えても応力が低下せず、増加します。
以上の説明から、下図4は真応力-ひずみ曲線と公称応力-ひずみ曲線の違いを定性的に表したものです。
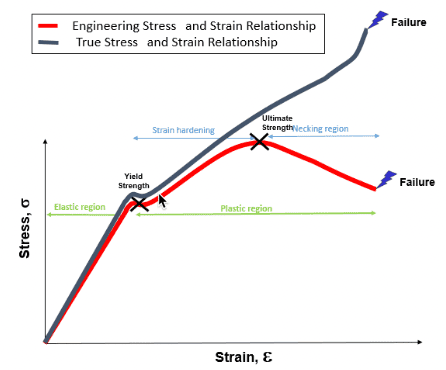
図4: 工学的応力-ひずみ曲線と真の応力-ひずみ曲線 [3]
工学的応力-ひずみ特性と真の応力-ひずみ特性の関係を下表にまとめます:
パラメータ |
公称応力 |
真応力 |
| 応力 | $$\sigma_e=\frac{F}{A_0}$$ | $$\sigma_t=\frac{F}{A_t}$$ |
| ひずみ | $$\epsilon_e=\frac{L-L_0}{L_0}$$ | $$\epsilon_t=\ln \left(\frac{A_0}{A_i}\right)=\ln \left(\frac{L_0}{L_i}\right)$$ |
| ここで | \(\sigma_e\) = 公称応力 \(\sigma_t\) = 真応力 F = 力 A0= 初期断面積 Ai= 瞬間断面積 \(\epsilon_e\) = 公称ひずみ \(\epsilon_t\) = 真ひずみ L0 = 初期ゲージ長さ Li = 瞬間ゲージ長さ L = 変形ゲージ長さ |
一般的に、真応力とひずみの関係は、負荷がかかったときの材料の挙動をより現実的に表現します。数値シミュレー ションでは真応力-ひずみ関係を材料特性として用いることがよくあります。公称応力-ひずみ曲線を真応力-ひずみ曲線に変換するには、以下の公式を使用します:
$$\sigma_t=\sigma_e \left(1+\epsilon_e\right)$$
$$\epsilon_t=\ln \left(1+\epsilon_e\right)$$
応力-ひずみ線図の各段階
上の図3に見られるような段階は、次のように対処できます:
1)応力-ひずみ関係は弾性領域では線形です。この段階では、荷重を取り除くと材料は常に元の位置に戻ります。また、弾性領域では材料がフックの法則に従うため、応力とひずみは互いに比例します。直線の傾きは、ヤング率または弾性率として知られる材料の重要な特性を定義します。
$$E=\frac{\sigma}{\epsilon}$$
2)荷重が増加すると、材料の挙動は弾性領域から塑性領域へと移行します。この移行が起こる応力を降伏応力と呼びます。降伏応力を超えると、材料の変形は永久的なものになります。簡単に言えば、弾性ひずみは回復可能ですが、塑性ひずみは回復不可能です。
3)降伏点を特定することは必ずしも明らかではありません。従って、有効かつ従来の近似的な方法は、直線勾配を0.2%ひずみ分オフセットすることです。応力-ひずみ曲線との交点が降伏点を定義します。
4)降伏後、材料はひずみ硬化または加工硬化を受け、その結果、材料は変形するにつれて強くなります。応力-ひずみ曲線が降伏応力を超えて最大引張応力に達するまで増加するのは、基本的にこのためです。
5)ネッキングの過程で、材料は不均一な塑性変形を起こします。試料の一部分が薄くなり、その部分に非常に高い応力が集中して破壊に至ります。破断後、伸び率と断面積の減少率を計算することができます。ネッキングの段階では、収縮領域が考慮されないため、工学的応力が減少する一方で、真の応力は増加し続けることは注目に値します。
6)破断点におけるひずみは、試験片の全伸びを定量化します。ここで、伸びの程度は材料の延性を示します。延性の高い材料は、より大きな塑性変形に耐えることができます。一方、降伏点付近の破壊ひずみを持つ材料は脆性材料と見なされます。
さまざまな材料の応力対ひずみ曲線
応力-ひずみ曲線は材料や材料系列によって大きく異なります。主に延性材料と脆性材料に大別されます。図5はこの2つの違いを示しています。
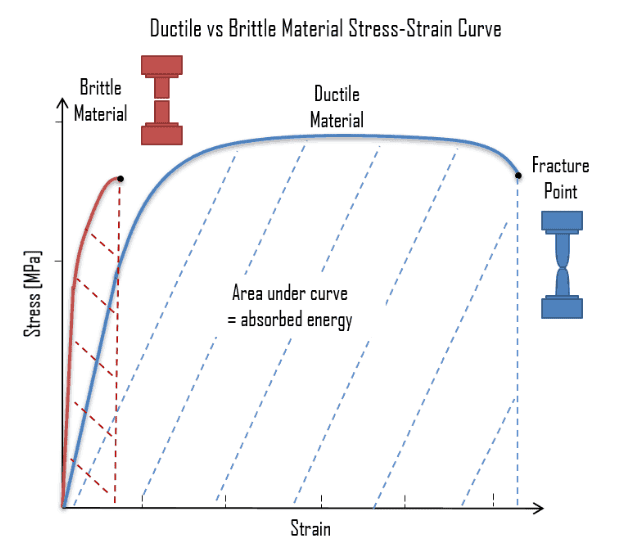
図5: 延性材料と脆性材料の挙動 [4]
延性材料は、降伏能力によってかなりのエネルギーを吸収することができます。このため、材料は破壊する前にかなりの塑性変形に耐えることができます。延性材料の典型的な応力-ひずみ曲線には、上述した応力-ひずみ曲線の段階が含まれます。延性材料の例としては、軟鋼、アルミニウム、銅、ゴム、およびほとんどのプラスチックが挙げられます。
一方、脆性材料は伸び率の顕著な変化なしに破断します。つまり、降伏強さ、極限強さ、破壊強さはすべて同じです。鋳鉄、セラミック、ガラス、コンクリート、石などが脆性材料の例です。
図6に様々な材料の応力-ひずみ曲線の例を示します。グラフの下に列挙されている材料が、その特定の種類の材料すべてを代表しているわけではないことに注意が必要です。荷重下での材料の挙動には、材料組成、熱処理やコンディショニング、温度、引張試験のひずみ速度など、複数の要因が影響します。
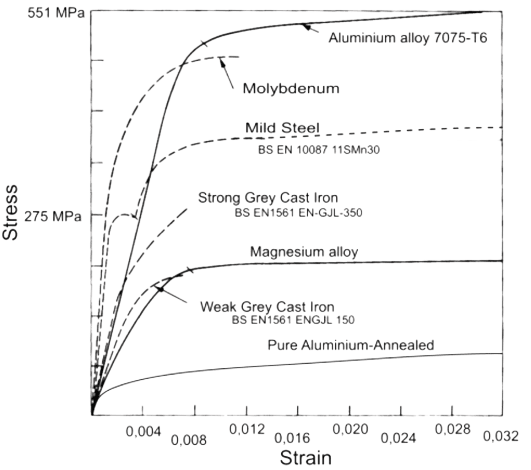
図 6: 異なる材料タイプの応力-ひずみ曲線 [5]
参考
- https://en.wikipedia.org/wiki/File:Tensile_test_-_steel_sample.ogv
- https://www.admet.com/effect-specimen-geometry-tensile-testing-results/
- https://yasincapar.com/engineering-stress-strain-vs-true-stress-strain/#:~:text=The%20curve%20based%20on%20the,the%20true%20stress%2Dstrain%20curve
- https://www.nuclear-power.com/nuclear-engineering/materials-science/material-properties/toughness/ductile-material-ductile-fracture/
- https://www.roymech.co.uk/Useful_Tables/Mechanics/Stress_Strain_diagram.html
SimScale製品紹介資料ダウンロード

資料請求
資料全体をご希望の方はこちらのフォームからお申し込みください。