主応力と主ひずみは、構造工学と設計における基本的な概念であり、材料と構造物の評価と解析を支えています。様々な用途の安全性と安定性に不可欠なこれらの用語は、外部荷重を受けた際に材料が受ける内部力と変形を反映しています。これらの概念を理解することの重要性は、専門家が設計における潜在的なリスクを評価し、軽減することを可能にするツールである主応力式と主ひずみ式の応用にも反映されています。

この概説では、これらの用語の本質、数学的定式化、および実世界のシナリオにおける意味を探ります。また、モールの応力円などの関連概念や、フォンミーゼス応力と主応力の区別についても説明します。これらの基本原理を理解することで、専門家は土木インフラから高度な航空宇宙部品に至るまで、設計の構造的完全性を確保することができます。

主応力とは

主応力とは、複雑な荷重条件にさらされた場合に材料内で発生する最大および最小の法線応力を表します。この概念を理解することは、材料の応答と潜在的な弱点に関する洞察を得る上で不可欠です。材料が多方向の応力を受ける場合、主応力を決定することで最も深刻な応力集中を明らかにすることができ、これは構造的な不具合を回避する上で非常に重要です。

最大応力$\sigma_1$と最小応力$\sigma_2$の主応力公式は[1]で与えられます:

$$ \sigma_1 = \frac{(\sigma_x + \sigma_y)}{2} + \sqrt{\left(\frac{\sigma_x – \sigma_y}{2} \right)^2 + (\tau_{xy})^2} $$

$$ \sigma_2 = \frac{(\sigma_x + \sigma_y)}{2} – \sqrt{\left(\frac{\sigma_x – \sigma_y}{2} \right)^2 + (\tau_{xy})^2} $$

ここで、$\sigma_x$と$\sigma_y$はx方向とy方向の法線応力、$\tau_{xy}$ はせん断応力です。

主応力の重要性は、特に主応力の公式を使用した計算を掘り下げてみるとよくわかります。この式は平衡力学と材料力学に根ざしており、材料が受ける応力を正確に表現します。主応力方程式は、設計が最適であるだけでなく安全であることを保証します。

しかし、材料が受け得る究極の応力とは何でしょうか？これが最大主応力の概念につながります。この値を認識することは、材料が受ける応力の最高レベルを指定するため、破壊解析にとって極めて重要です。構造工学や設計では、最大主応力を理解することが、耐久性があり長持ちする構造体と、間近に迫った破壊との分かれ目になります。

コーシー応力テンソル

コーシー応力テンソルは、単に応力テンソルと呼ばれることも多く、主応力と密接に関連する基礎的な概念です。応力テンソルは、材料要素内の応力状態を包括的に表現します。基本的に、応力テンソルは、変形可能な物体内の平面のすべての可能な方向に作用する法線応力とせん断応力の大きさと方向の両方を記述します。

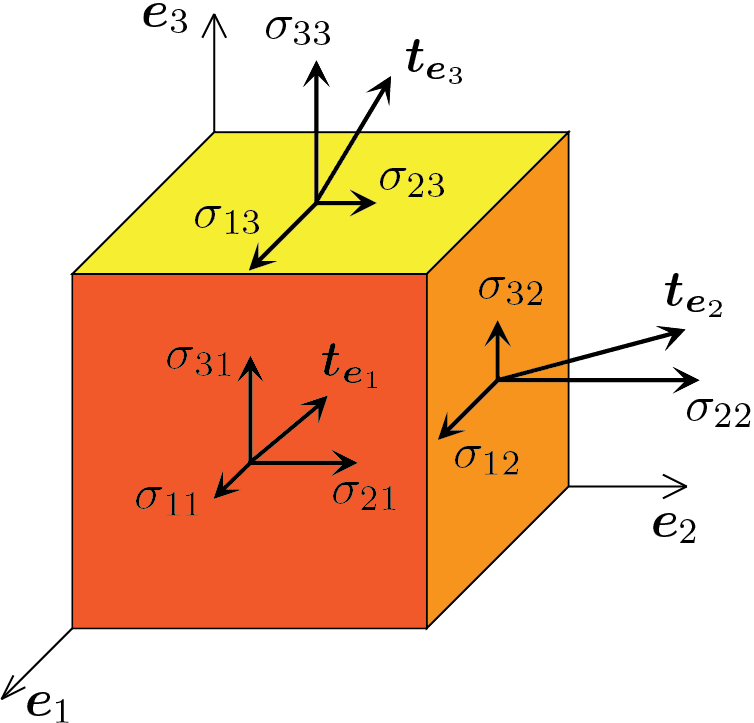
図1: コーシー応力テンソルの表現[2]

応力テンソルを理解することは、主応力をさらに導き出すための基礎となるため、非常に重要です。応力テンソルを対角化することで、材料内で最も応力がかかっている状態と最も応力がかかっていない状態を強調する主応力値を決定することができます。このような変換プロセスは、特に複雑な応力シナリオを検討する際、最大応力の真の性質と方向を特定するのに役立つため、極めて重要です。

構造解析の領域では、コーシー応力テンソルとその主応力との関係から得られる情報を活用することで、エンジニアは材料の安全性、性能、および設計変更について十分な情報に基づいた決定を下すことができます。

モールの応力円

応力解析のグラフィカルな表現として一般的に使用されるモールの応力円は、エンジニアにとって不可欠なツールです。この 2 次元図法を使用すると、応力変換を視覚的に明確に解釈できるため、材料の法線応力とせん断応力の関係が明確になります。

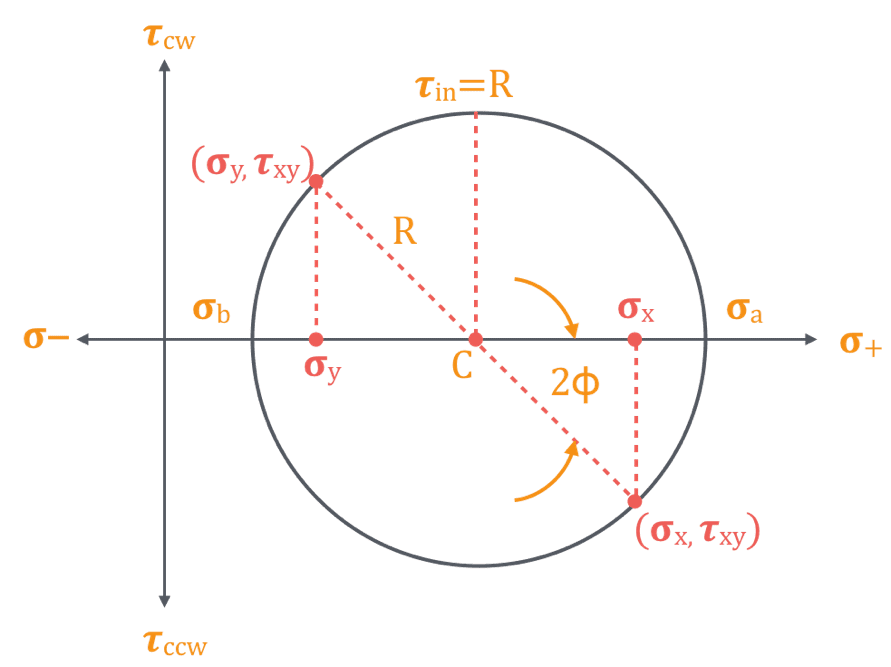
図 2: 主応力と最大せん断応力を示すモールの円[3]

モールの円は単なる可視化手法ではなく、主応力の中核概念を理解するための橋渡し役です。法線応力とせん断応力を円上にプロットすることで、最大主応力とそれに対応する方位を簡単に特定することができます。また、円の半径から、結果として生じる応力の大きさを知ることもできます。

モールの円はひずみ解析にも使用できるため、主ひずみの計算にも関連します。このグラフ表示を理解し、正しく解釈することは、特に設計の安全性と機能性にとって最も重要な応力状態を決定する際の鍵となります。

構造工学の分野が進化を続ける中、モールの応力円は、古くから伝わる原理と最新の解析技術を結びつける不動のツールであり続けています。

主応力とフォンミーゼス応力の比較

構造解析の領域では、破壊を理解し予測するためのさまざまな基準が提供されていますが、そのうちの 2 つが主応力とフォンミーゼス応力です。どちらも荷重下での材料の挙動を理解することを目的としていますが、その目的は異なり、別々の理論に基づいています。

主応力は、要素に作用する法線応力の最大値と最小値として見ることができ、材料が経験する主要な引張応力と圧縮応力に関する重要なデータを提供します。脆性材料を解析する場合、これらの応力は潜在的な破壊点を示すため、これは特に重要になります。

一方、等価応力または歪みエネルギー応力としても知られるフォンミーゼス応力は、特に延性材料の降伏につながるエネルギーに重点を置いています。これは降伏の開始を予測することを目的とした派生値であり、材料内の実際の応力成分を表すものではありません。

主応力とフォンミーゼス応力を比較する際には、それぞれの長所を認識することが重要です。脆性材料では主応力基準が優先されることが多く、延性材料ではフォンミーゼス応力が優先されます。

主ひずみとは？

主ひずみとは、荷重を受ける材料に発生するひずみの最大値と最小値を表します。ひずみを理解することは、材料の変形、つまり加えられた応力に対して材料がどれだけ伸び縮みするかについて洞察する上で非常に重要です。

一般的にひずみは、寸法の変化を元の寸法で割った値として定義されます。数学的には、法線ひずみ($\varepsilon$ )は[4]のように表すことができます:

$$ \varepsilon = \frac{\Delta L}{L_0} $$

$\varepsilon$ は線形ひずみまたは法線ひずみ、

$\Delta L$ は材料または物体の長さの変化、

$L_0$ は材料または物体の元の長さまたは初期の長さです。

最大主ひずみの概念は、特に極端な荷重条件下での材料の挙動を評価する場合など、設計上の検討において極めて重要です。このひずみ値は、材料が受ける最大の伸縮に関するデータをエンジニアに提供し、多くの場合、材料の潜在的な破壊の指標となります。

このトピックを深く掘り下げるには、主ひずみの式と方程式を理解することが有益です。主ひずみも主応力と同様に、せん断ひずみがゼロの面で発生します。主ひずみを求める方程式は、材料のある点におけるひずみの状態に依存するため、複雑になることがあります²:

$$ \varepsilon_1 = \frac{(\varepsilon_x + \varepsilon_y)}{2} + \sqrt{\left(\frac{\varepsilon_x – \varepsilon_y}{2} \right)^2 + \left(\frac{\gamma_{xy}}{2} \right)^2} $$

$$ \varepsilon_2 = \frac{(\varepsilon_x + \varepsilon_y)}{2} – \sqrt{\left(\frac{\varepsilon_x – \varepsilon_y}{2} \right)^2 + \left(\frac{\gamma_{xy}}{2} \right)^2} $$

$\varepsilon_1$ と$\varepsilon_2$はそれぞれ最大主ひずみと最小主ひずみです。

$\varepsilon_x$ と$\varepsilon_y$ は x 方向と y 方向の法線ひずみで、

$\gamma_{xy}$ は工学的なせん断ひずみです。場合によっては、このせん断ひずみは主ひずみの式で使用される値の半分として表されることがあるため、正しい定義を使用することが非常に重要であることに注意してください。

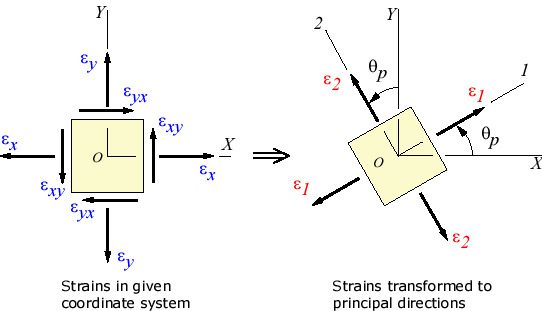
図3: 法線ひずみから主ひずみへの変換[5]

最大主ひずみを認識し計算することは、材料と構造物の安全性を確保するために不可欠であり、潜在的な破壊を予測し防止するための指標となります。

エンジニアリングにおける応用

エンジニアリングの世界では、主応力と主ひずみを理解することは理論的な必要性だけでなく、実際的な必要性でもあります。これらの概念は、構造物の設計、解析、および最適化において中心的な役割を果たします。特に構造工学と設計の分野では、これらの主応力と主ひずみの値を計算することで、安全マージンを示すだけでなく、設計の最適化の可能性をより深く理解することができます。

例えば土木工学。橋や高層ビルを建設する際には、構造物の重量、構造物に作用する力、使用する材料の間で常にバランスを取る必要があります。最大主応力などの値を参照することで、エンジニアは不具合が発生する可能性のある箇所を予測し、それを回避するための設計を行うことができます。

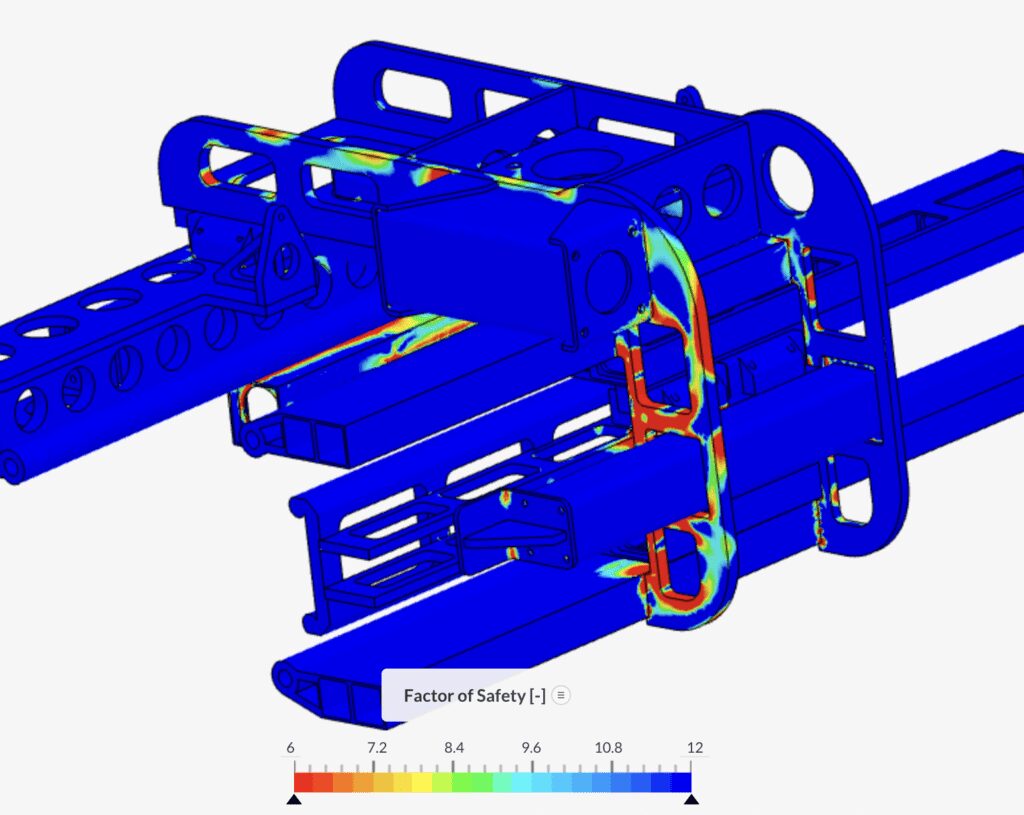
図3: トラス橋の解析結果

航空宇宙エンジニアにとって、そのリスクは非常に高いものです。航空機の部品は、離着陸時の力から高高度での圧力まで、さまざまな応力にさらされています。主ひずみ式を使用することで、これらの条件下で航空機の部品がどのように変形し、形状が変化するかを評価し、空の安全を確保することができます。

また、大きな構造物や航空機だけではありません。自動車業界では、自動車の軽量化と低燃費化が進んでいます。しかし、自動車は安全でなければなりません。エンジニアは、多くの場合、主応力方程式を使用して自動車部品の試験と設計を行い、経済的で効率的でありながら路面からの応力に対応できるようにしています。

図5: スプリング上の応力分布を示す自動車のサスペンションシミュレーション

全体として、さまざまな工学分野にわたって、主応力とひずみの応用は膨大かつ重要です。主応力とひずみは意思決定の指針となり、最終設計における安全性と性能の両方を保証します。

最新の解析におけるシミュレーション

今日のデジタル時代において、コンピュータシミュレーションの威力は、工学的課題へのアプローチ方法に革命をもたらしています。主応力と主ひずみの解析は、最新の計算ツールにより、より正確で効率的、かつ詳細になりました。

このようなツールが登場する以前は、エンジニアは手計算や小規模な物理試験に頼らざるを得ませんでした。現在では、シミュレーションによって、構造物が建設される前であっても、構造物がさまざまな力に対してどのように反応するかを包括的に把握することができます。ソフトウェアプラットフォームにより、エンジニアは仮想的に荷重を加え、応力分布を解析し、潜在的な破壊点を予測することができます。

このようなプラットフォームの代表的な例がSimScaleです。SimScaleの有限要素解析機能は、複雑な構造物の主応力とひずみを評価する動的環境を提供します。このツールを使用することで、エンジニアは、コストや時間がかかりすぎたり、物理的なテストが不可能なシナリオを評価することができます。

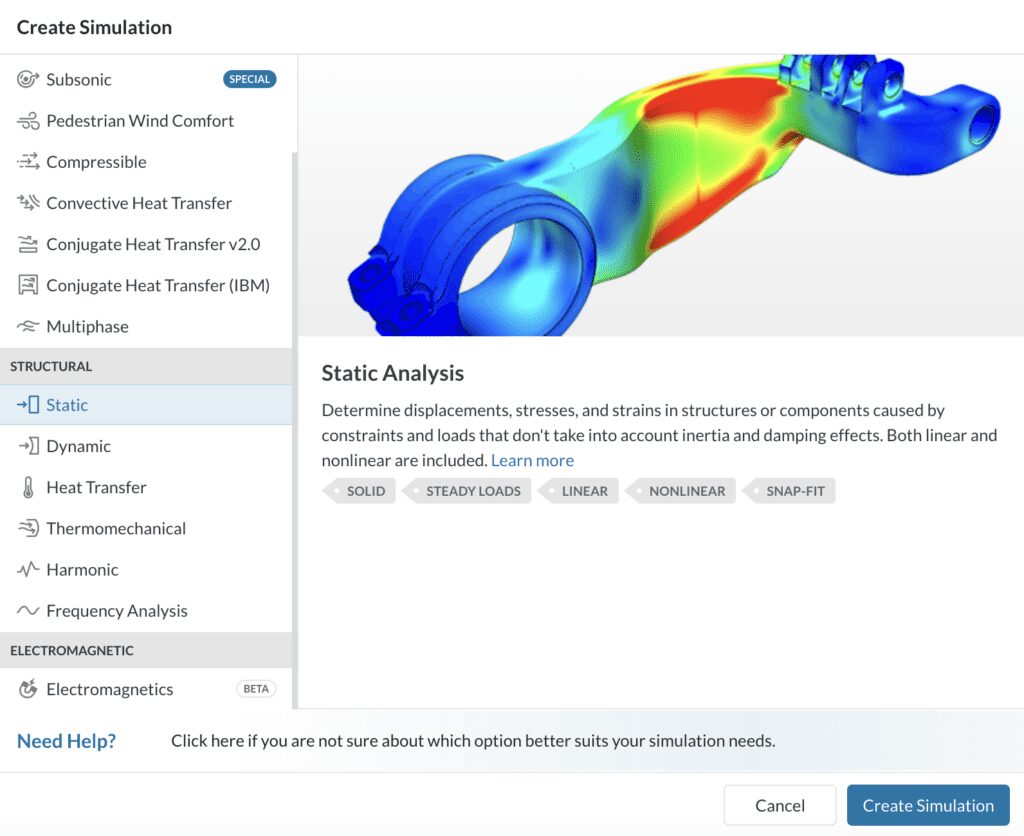
図6: SimScaleの解析タイプライブラリでは、プロジェクトに適したシミュレーションソルバーを選択できます(FEA/構造ソルバーなど)

シミュレーションツールの重要な利点の1つは、複雑な形状や多面的な荷重条件下での最大主応力とひずみに関する知見を提供できることです。このような深い解析により、エンジニアは設計を最適化し、構造物をより安全で効率的なものにすることができます。

さらに、フォン・ミーゼス応力と主応力に関する議論は、シミュレーション・プラットフォーム上で可視化することでより豊かになります。明確なビジュアル表示により、エンジニアは異なる応力値を比較し、材料選択、設計変更、安全係数について十分な情報に基づいた決定を下すことができます。

要するに、シミュレーション技術と主応力および主ひずみの原理の融合が、エンジニアリング解析の未来を形成しているのです。シミュレーションは時間とリソースを節約するだけでなく、設計と技術革新の可能性の限界を押し広げます。

参考

Bilotta, A., “Cauchy stress tensor tensor”, A first course on solid mechanics, Available at: https://antoniobilotta-structuralengineer.github.io/MyWebSite/SMbook_en/stress_sec_stress_chap_en.html
Beer, F. P., Johnston, E. R., DeWolf, J. T., & Mazurek, D. F. (2020). Mechanics of Materials (8th ed.). New York: McGraw-Hill.
https://blog.prepineer.com/how-to-construct-a-mohrs-circle/
Timoshenko, S.P., & Goodier, J.N. (1982). Theory of Elasticity (3rd ed.). New York: McGraw-Hill.
efunda, Calculators: Principal Strain, Available at: https://www.efunda.com/formulae/solid_mechanics/mat_mechanics/calc_principal_strain.cfm

2024年3月13日