時間調和解析の原理や、低周波近似、また近似が適用可能な現象や用途について、図解とともにわかりやすく解説します。
電磁気現象は一般にマクスウェル (Maxwell) 方程式によって記述されます。線形材料と時間調和励起 (つまり、正弦または余弦の時間依存性を持つ励起) の場合、電場、磁場、およびすべての電流も時間調和です。時間調和とは、時間とともに周期的に変化する現象を指します。この時、マクスウェル方程式は角周波数\({\omega}\)を持つ時間調和形式で記述できます。
$$ {\nabla} \times \mathbf{H}=\mathbf{J}_{free}+i{\omega}\mathbf{D}, \tag{1a}$$
$$ {\nabla} \times \mathbf{E}=-i{\omega}\mathbf{B}, \tag{1b}$$
$$ {\nabla} \cdot \mathbf{D}={\rho}_{free}, \tag{1c}$$
$$ {\nabla} \cdot \mathbf{B}=0. \tag{1d}$$
この方程式では電場(電界の強さ)は\(\mathbf{E} \)、磁気誘導または磁束密度\(\mathbf{B} \)、誘電変位\(\mathbf{D} \)、磁場の強さ\(\mathbf{H} \)、自由電流密度\(\mathbf{J}_{free} \)と示され、時間に依存しない複素ベクトル場です。例えば、時間依存の電場は、関係式\(\mathbf{E}(x, t)={Re}(\mathbf{E}(x)e^{i{\omega}t})\)で得られます。他の場についても同様です。
これらの方程式は、以下の\(\mathbf{B} \)と\(\mathbf{H} \)、\(\mathbf{E} \)と\(\mathbf{D} \)そして\(\mathbf{J} \)に関連する構成方程式によって完成されます。これらの巨視的な法則により、微視的な電荷と電流の詳細な記録は必要ありません。単純な材料の場合、以下の式で表されます。
$$ \mathbf{D}={\epsilon}\mathbf{E} \tag{2a}$$
$$ \mathbf{B}={\mu}\mathbf{H} \tag{2b}$$
$$ \mathbf{J}={\sigma}\mathbf{E} \tag{2c}$$
ここで、\( {\sigma} \)は電気伝導率で、\({\epsilon}={\epsilon}_0{\epsilon}_r \)、\({\mu}={\mu}_0{\mu}_r \)です。ただし、無次元定数\({\epsilon}_r \) (比誘電率)、\({\mu}_r \) (比透磁率) は物質によって異なります。真空の場合、そして空気の場合は次のように示せます。「\({\epsilon}_r={\mu}_r=1 \)」
時間調和電磁気学 (AC磁気学)
以下のセクションで説明する条件下では、\(i{\omega}\mathbf{D} \)で表される変位電流項は式(1a)から省略することができる。残りのモデルは以下のようになる。
$$ {\nabla} \times \mathbf{H}=\mathbf{J}_{free}, \tag{3a}$$
$$ {\nabla} \times \mathbf{E}=-i{\omega}\mathbf{B}, \tag{3b}$$
$$ \mathbf{J}={\sigma}\mathbf{E}, \tag{3c}$$
$$ \mathbf{B}={\mu}\mathbf{H}, \tag{3d}$$
上記のモデルは、マクスウェル方程式の低周波近似と呼ばれ、準静的近似とも呼ばれます。
磁束密度の発散を表す式(1d)は不要であり、時間調和モデルには含まれていないことに注意してください。これは式(3b)によって導かれるためです。式(3b)の発散をとれば、回転の発散はゼロであるため、式(1d)が成り立つことが分かります。
この近似解は、計算領域全体における磁場と誘導、そして導体内の電流と電場を与えます。非導体内の電場も知りたい場合は、非導体領域における追加の発散方程式を解く必要があります。これにより、非導体領域における電荷に関する情報が得られます。完全なマクスウェル方程式に対する近似方程式(3a~3d)の利点は、巧みに行えばより簡単かつ迅速に解くことができることです。
適用範囲
これらはすべて近似値であるため、次のような疑問が生じます。
どのような条件であればこの近似は成立するのでしょうか?また、どのような目的でこの近似が正しく使われるのでしょうか?
基本的に、これは低周波近似値です。つまり、このモデルは十分に低い周波数でのみ有効です。ただし、ここで言う「十分に低い」とは状況によって異なります。1Hzの場合もあれば、1GHzの場合もあります。そこで、妥当となる条件を詳しく見ていきましょう。
近似によって生じる誤差が小さくなるためには、以下の3 つの条件を満たす必要があることが分かっています1。
- 計算領域は波長に比べて小さいこと。言い換えれば、電磁場が計算領域を伝播するのにかかる時間は励起の周期よりもはるかに短くなければならず、励起の変化はどの場所でも瞬時に認識できる必要があります。
- 導体は高い導電性を持っていること。つまり、\(\omega\epsilon \|| \sigma \)であることです。ただし、\(\epsilon \)は誘電率です。これは電場の変化に対し導体内に電荷が蓄積されず、静電容量が無視できることを意味します。
最初の条件では、たとえば、アンテナや波の伝播を説明できないことを意味し、最後の条件は、共振回路と共振効果も近似の適用範囲外であることを意味します。ただし、モーター、発電機、変圧器など、この近似で非常によく説明できる重要なアプリケーションは数多くあります。
基本的に、これらの近似は磁気エネルギーの変化が電気エネルギーの変化よりもはるかに大きく、誘電効果が作用する場合に使用できます。なぜなら、式(3b)は有名なファラデーの電磁誘導の法則に他ならないからです。これは、誘導渦電流、表皮効果、近接効果といった現象が正しく記述されることを意味します。
誘導渦電流
電磁誘導の法則により、変化する磁場は電場を発生させます。電場の位置に導体がある場合、電流が流れ、自己完結して渦を形成します。そのため、これらの電流は渦電流と呼ばれ、その基礎となるモデルは渦電流モデルとも呼ばれます。
金属板などの導体が変化する磁場にさらされると、導体を通過する磁束は時間とともに変化します。その結果、ファラデーの電磁誘導の法則に従い、導体に起電力 (EMF) が誘導され、渦電流が発生します。
これらの電流は導体内を閉ループ状に循環し、元の磁場の変化に逆らう局所的な磁場を生成します。一般的に、磁場の強度や方向の変化につながるあらゆる要因は、導体内に渦電流の発生を引き起こす可能性があります。
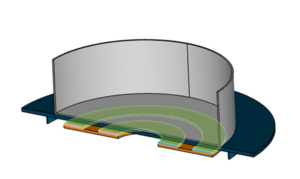
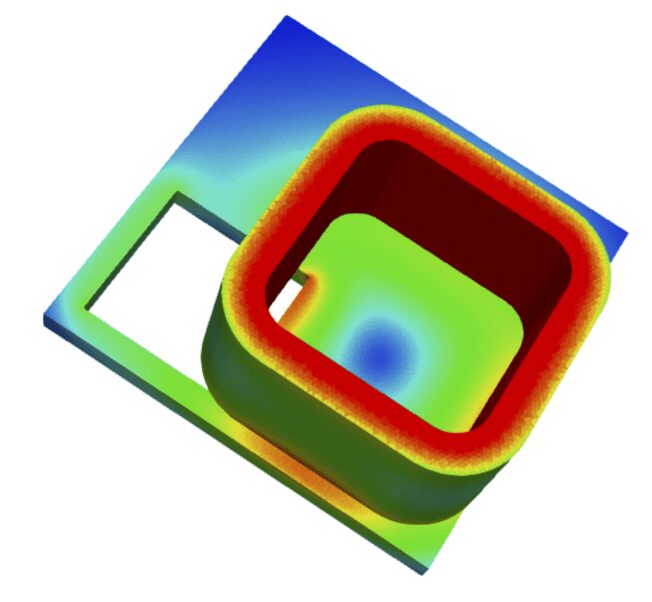
下の図は、よく知られているベンチマークモデル (TEAM 7) を示しています。これは、渦電流を誘導する穴が開けられたアルミニウム板の上にコイルを配置したものです。このベンチマークモデルは、電磁気コードの検証に使用されます。
表皮効果
表皮効果は、電気導体が交流 (AC)、特に高周波にさらされた際に顕著に現れる現象です。AC電流が導体を流れる際、電流は断面全体に均一に分布するのではなく、表面付近に集中する傾向があります。この周波数依存の挙動は、導体の実効抵抗の増加につながります。周波数が高くなると、電流の大部分は表面近くの薄い層に閉じ込められ、直流 (DC) 状態と比較して抵抗が高くなります。
電流が導体に浸透する深さは表皮深さとして定義され、周波数の平方根と材料の導電率に反比例します。表皮効果により、表面付近に集中する電流によって抵抗が増加します。これは熱という形での電力損失の増加に寄与するため、特に高周波交流信号を扱う電気システムの設計において重要な考慮事項となります。
エンジニアたちは、電流の流れを効率化するために、中空導体や複数の絶縁された細い線を束ねたリッツ線などを使って、実質的な導電面積を広げる工夫をすることがよくあります。

近接効果
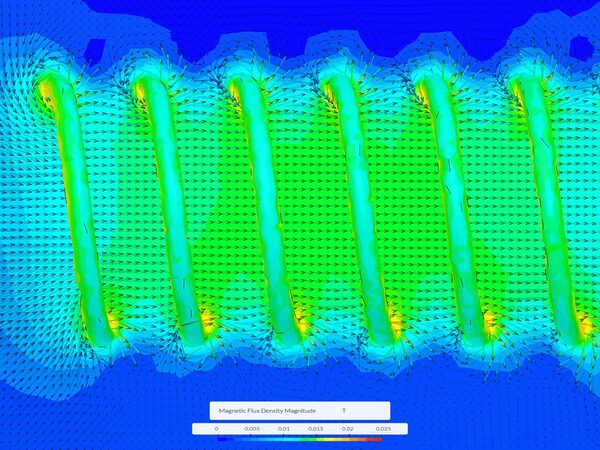
表皮効果は主に一導体の外層に影響を及ぼすのに対し、近接効果は交流電流が流れる近接した平行導体において観察される現象です。これは、1 本の導体を取り囲む磁場が隣接する導体と相互作用し、電流の再分配を引き起こす傾向を表します。
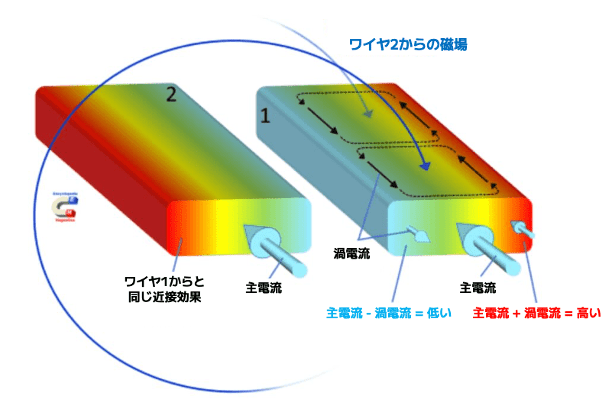
近接効果とは、周波数が高くなるにつれて、導体表面上で接線方向の磁界強度が最も強い箇所に電流が集中する現象を指します。例えば、電流の方向が反対の2つの導体が互いに近接している場合、導体間の磁界は外側よりも強くなり、電流はもう一方の導体に面した側に集中します。
高周波では、交流電流によって1本の導体に発生する交流磁界が、隣接する導体に渦電流を誘導します。これにより、隣接する導体に面する側に電流が集中し、各導体内で電流分布が不均一になります。近接効果は、導体間の距離が表皮深さと同程度かそれより小さい場合に最も顕著になります。
表皮効果と同様に、近接効果は実効抵抗を増加させ、システムにおける電力損失の増加に寄与します。これらの影響に対処するために、導体間隔の調整や、影響を最小限に抑えるための特定の幾何学的構成の採用など、緩和策が講じられています。さらに、近接効果は、高電力送電線や密集したケーブルの設計において重要な考慮事項です。
時間調和解析の応用
ここでは、時間調和解析によって正しくモデル化できる応用例をいくつか示します。さらに詳しい例については、「電磁誘導とは」も参照してください。
変圧器 (トランス)
変圧器は電気工学の分野で欠かせない装置であり、送電や配電システムの中核を担っています。変圧器は電磁誘導の原理に基づいて動作し、2つ以上の回路間で電気エネルギーを効率的に伝送します。電圧レベルを変換することで長距離送電を可能にし、電力網の機能に大きく貢献しています。
変圧器は、強磁性体でできたコアと、一次・二次巻線から構成される磁場を利用して巻線間に電圧を誘導します。この仕組みにより、電圧を昇圧・降圧することが可能となり、多様な電力供給のニーズに対応します。
変圧器には、小型の家庭用変圧器から大型の公共施設規模のユニットまで、さまざまなタイプとサイズがあり、それぞれが複雑な電気インフラ構造内の特定の要求を満たすように設計されています。
時間調和シミュレーションは、コア材料、巻線構成の最適化、磁場分布、損失、温度変化の予測 (熱ソルバーと組み合わせた場合。SimScaleに搭載予定) に非常に役立ち、電力システムの動的な環境下で効率的かつ信頼性の高い変圧器設計の開発に貢献します。
非破壊検査 (NDT)
非破壊検査 (Non-Destructive Testing: NDT) は、損傷を与えることなく材料の健全性を評価するために不可欠な技術です。低周波磁気近似に基づく2つの重要な手法は、交流磁場測定 (Alternating Current Field Measurement: ACFM) と渦電流検査です。
交流磁場測定は、強磁性材料に交流磁場を誘導し、漏洩磁束を解析することで表面および表面近傍の欠陥を検出します。この方法は非常に感度が高く、石油・ガス、航空宇宙、製造業などの業界で、パイプラインや溶接部などの重要部品の検査に広く用いられています。
一方、渦電流検査は、電磁誘導を利用して導電性材料の欠陥を検出します。交流電流により渦電流を発生させ、亀裂や導電率の変化など、欠陥によって引き起こされる障害を検出し、分析します。
渦電流試験は、表面および表面下の欠陥を特定し、損傷を与えることなく材料の健全性に関する結果を検出する能力があるため、航空宇宙、自動車、製造の各業界で広く使用されています。
交流磁場測定と渦電流試験はどちらも、さまざまなアプリケーションにわたって重要な構造とコンポーネントの品質と信頼性を確保する上で重要な役割を果たします。
バスバーの表皮効果
バスバーにおいては、表皮効果と呼ばれる現象が交流電流 (AC) の分布において重要な役割を果たします。前述のように、表皮効果は電流分布を不均一にし、導体表面へ電流の流れを集中させます。
交流周波数が高くなるほど、この影響は顕著になります。表皮効果は電流の有効断面積に影響を与えるため、特に高周波数環境では、バスバーの設計においてエンジニアは表皮効果を注意深く考慮する必要があります。最適な性能を確保するには、寸法の最適化が不可欠です。
誘導加熱
誘導加熱は、電磁誘導によって導電性材料を加熱する方法です。このプロセスは、電磁場が対象材料 (通常は金属) 内に電流を誘導するという原理に基づいています。コイルに交流電流を流すことで、急速に変化する磁場が生成されます。この磁場内に導電性材料を置くと、材料内に渦電流が誘導され、電気抵抗による抵抗加熱が発生します。誘導加熱は非常に高精度で、熱源に直接接触することなく、局所的かつ制御された加熱が可能です。
SimScaleにおける時間調和電磁界解析
SimScaleは、設計者が単一のプロジェクト内で幅広い物理シミュレーションを実行できるようにするマルチフィジックス・プラットフォームです。SimScaleでは電磁界解析ソルバーをリリースしており、現在は低周波をカバーしています。静磁場シミュレーションと時間調和解析機能を備えたSimScaleにより、エンジニアと設計者は様々な電磁気学シミュレーションを同時に実行できます。
これは、他の分析タイプと並行して実行することもでき、オールインワンの使いやすいオンライン ワークベンチで、ハードウェアの制限やソフトウェアのインストールに妨げられることなく、複数の物理現象を同時に計算することができます。
下のボタンをクリックして、SimScaleでシミュレーションを始めましょう。あなたの設計を、確信を持って次のステージへ進めるお手伝いをします。
SimScaleのクラウドネイティブ・プラットフォームなら、アカウントを作成するだけで数分でシミュレーションを開始できます。インストール不要・特別なハードウェア不要・クレジットカードも不要です。