浮力とは、流体が流体中の物体に及ぼす上向きの力のことです。
流体では、圧力は深さとともに増加します。したがって、物体が流体に浸かると、その底面にかかる圧力は上面にかかる圧力よりも高くなります。
この圧力の差により、正味の上向きの力(浮力)が生じます。この力は重力に対抗する力であり、物体の体積を占めるはずの流体の重さ、すなわち置換された流体の重さに相当します。
したがって、物体の密度が流体よりも小さければ、浮力はその重量よりも大きくなり、物体は浮きます。逆に、物体の密度が流体よりも大きければ、物体は沈みます。物体の浸漬部分の重量が、置換された流体の重量と同じであるとき、すなわち、密度が一致するときに平衡状態となります。
物体の密度は一般に、浸漬部分の質量と体積の単純な比としてとらえられることに注意してください。最も一般的なケースは、固体が液体の中に浸ること(例えば、海中の船)ですが、それだけではありません。上昇する気泡(液体中の気体)、落下する液滴(気体中の液体)、エアロスタット(暖かい空気が冷たい空気の中に入る)なども、浮力によって支配される現象の一例です。
流体力学における浮力
浮力の物理的原理は、シラクサのアルキメデスが紀元前3世紀に著した「浮体について」の中で初めて記述しました。アルキメデスの著書は、流体の物理学に関する観察と仮定を集めたもので、いわゆる「アルキメデスの原理」の定義につながりました。
アルキメデスの原理とは、「流体に全体的または部分的に浸された物体は、その物体によって変位した流体の重量に等しい力によって浮き上がる」というもの。
したがって、科学的方法が開発されるよりも何世紀も前に、アルキメデスは浮力に影響を与える2つの主な要因を指摘していたのです:
- 流体の密度
- 沈んだ物体の体積
流体の密度と水没した物体の体積の積は、「物体によって置換された流体の重量」を指します。

浮力効果: バランスと平衡
浮力は、流体中に沈んだ領域に見られる現象です。しかし、この領域が周囲の流体とは異なる特性(例えば、相が異なる、または同じ相でも密度が異なる)を持つ場合に、浮力は明らかになります。したがって、浮力の物理的基礎は、水没した体積の静的平衡から次のように導き出すことができます:
水没した長方形の体積
図2に示すように、長方形の体積が流体の中に沈んでいるとします。その寸法を水平方向に\(L_x\) 、垂直方向に\(L_y\) とすると、物体に作用するすべての力は、静水圧の境界面上の積分として計算できます:
$$ p=\rho g h \tag{1}$$
\(\rho\) は流体の密度。
\(g\) は重力加速度。
\(h\) は自由表面に対する深さ。
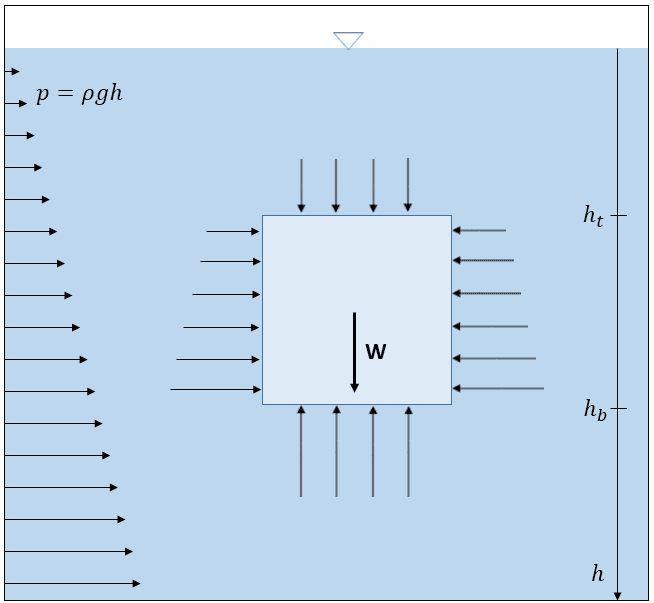
水平方向の平衡は、長方形の左側の面に作用する力と右側の面に作用する力の和として計算されます:
$$ F_x = \int_{h_b}^{h_t}p\,dh-\int_{h_b}^{h_t}p\,dh = \int_{h_b}^{h_t}\rho g h\,dh-\int_{h_b}^{h_t}\rho g h\,dh \tag{2}$$
すべての変数は、\(x\) 座標から独立していると見なされます。したがって、水平方向の平衡条件は自然に達成されます(すなわち、\(F_x≡ 0\) )。したがって、水平方向に対する浮力は見られません。
鉛直方向でも同じことができます:
$$ F_h = F_{buoyancy} – W=-\int_{L_x}p_t \, dx + \int_{L_x}p_b \, dx – W \tag{3}$$
\(L_x\) は長方形の水平寸法。
\(W\) は物体の重さ。
\(p_t\) と はそれぞれ長方形の上部と下部の圧力です。\(p_b\)
式(3)は次のように展開できます:
$$ F_h = -\int_{L_x}\rho g h_t \, dx + \int_{L_x} \rho g h_b \, dx – g\rho_{object}V_{object}$$
$$ =-\rho g h_t L_x + \rho h_b L_x – g \rho_{object}L_x L_y=\rho L_x (h_b-h_t)-L_x L_y g \rho_{object}$$
$$ =\rho g L_x L_y – L_x L_y g \rho_{object}=gL_x L_y (\rho – \rho_{object}) \tag{4}$$
式(4)から、浮力支配現象の主な特徴をすべて推論することができます:
- 浮力は、移動する流体の重量に依存し、流体自体の密度(\(\rho\) )と物体の水没部分の体積(この場合は\(L_xL_y\) )に依存します。
- 浮力は重量と反対向きの力です。
- 物体は
- 周囲の流体より密度が低い場合は浮く (\(F_h>0\))
- 密度が高ければ沈みます (\(F_h<0\))
- 周囲の流体と密度が同じ場合、完全な平衡状態を保ちます (\(F_h=0\))
連続体の無限小体積
有限の2次元正方形オブジェクトの手順は、一般的な無限小体積に拡張することができ、任意の界面形状と流体力学の問題に使用することができます。連続体の無限小部分の平衡は微分方程式で与えられます:
$$ f+div(\sigma)=0 \tag{5}$$
\(f\) は外力密度。
\(\sigma\) はコーシー応力テンソル。
この場合、体積外力は重力(体重)だけなので
$$ f=\rho g \tag{6}$$
浮力の総和を計算するには、浸漬された体積との界面で流体によって及ぼされるすべての表面力を合計する必要があります。これらの力は、応力テンソルによって次のように導出できます:
$$ t^n=n\cdot \sigma \tag{7}$$
\(n\) は表面に対する単位長さの法線。
\(t^n\) は、 \(n\)によって定義される無限小表面上の流体によって及ぼされる表面力です。\(n\)
有限次元表面上に及ぼされる力の合計を求めるには、体積境界上で\(t^n\) を積分する必要があります:
$$ F_{buoyancy}=\int_S t^{n}\, dS = \int_S n \cdot \sigma \, dS \tag{8}$$
ガウスの定理を適用すれば、表面積分は体積積分に変換できます:
$$ F_{buoyancy}=\int_V div(\sigma)\, dV \tag{9}$$
したがって、式(5)と式(6)を式(9)に代入すると、浮力の合計値が得られます:
$$ F_{buoyancy}=-\int_V f\, dV=-\rho g \int_V \, dV \tag{10}$$
\(V\) は流体領域中の体積で、符号"\(-\)"は重力に逆らうことを意味します。
\(\rho\) と\(g\) は簡単のために流体中で一様とみなされ、積分から取り除かれていることに注意してください。
式(10)は、アルキメデスが提案し、式(4)のケースで得られたのと同じ原理を再び述べています。
流体中に浸された体積の静的または動的バランスを解析するには、浮力だけでは必ずしも十分ではないことに注意することが重要です。
例えば、表面張力は流体と物体の界面に加わる付加的な力であり、問題の力学(例えば物体が沈む)と静力学(例えば物体が沈む)の両方に影響します。浮力の力学は、流体の粘性や流れの乱れにも大きく影響されます。
また、時間的に一定で空間的に一様であるとは限りません。次のようなことが変化する可能性があります:
- 流体と物体の界面(例: 水中を上昇中の気泡の変形)
- 密度(例えば温度変化による)
- 流体中の体積(例えば、流体の外側を移動する浮遊物体が、流体中の体積を減少させる)。
これらの理由から、浮力は通常、ナビエ・ストークス方程式で記述される流体力学問題の一部としてのみ考慮されます。ナビエ・ストークス方程式では、浮力は流体領域における密度の不均一性によって自然に考慮されます。
しかし、このケースの実装は通常簡単ではありません。したがって、多くの場合、浮力は体積外力としてモデル化し、慣性計算では密度を一定とみなします。この近似は「ブシネスク近似」と呼ばれています。この近似は、密度の変化が温度変化に起因する自然対流現象のモデルによく用いられます。
浮力の応用
前述したように、浮力は固体-液体(例えば、水中の船)の場合だけに言及すべきではありません。自然対流と混相流について注意深く考慮する必要があります。
自然対流における浮力効果
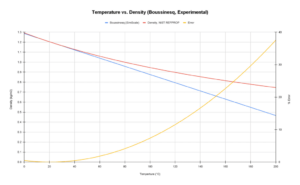
自然対流は、物質が温度の上昇とともに密度が低くなるという事実に基づいています(図3参照)。
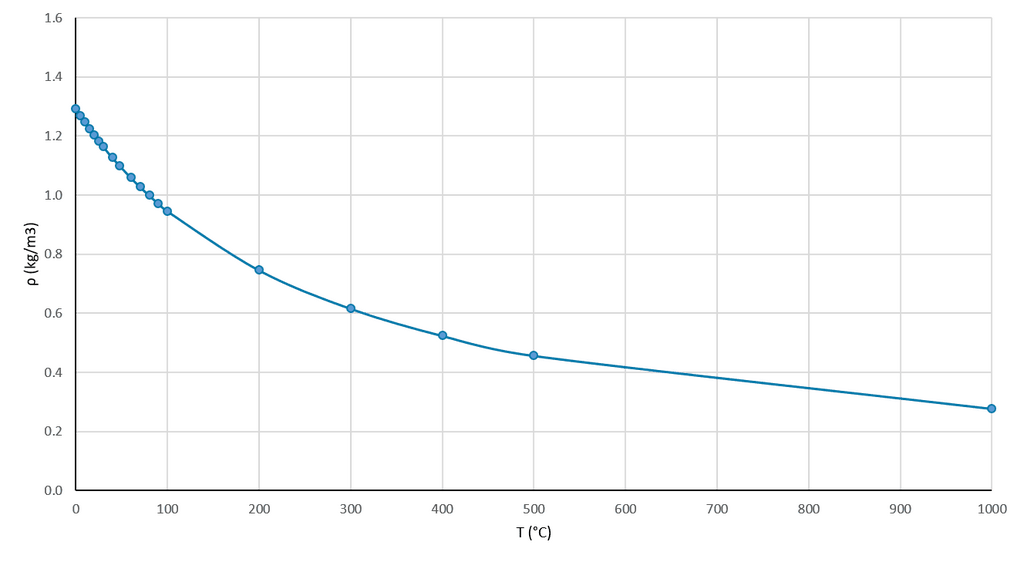
つまり、暖かい流体は、同じ流体でより冷たい領域に浸すと「浮く」ことになります。この場合、「浮く」とか「沈む」という言い方ではなく、熱い流体の上向きの流れと冷たい流体の下向きの流れという言い方をします。この現象は通常、熱解析と結びついており、気象学、鉄鋼鋳造、家屋の冷暖房など、多くの応用の基礎となっています。
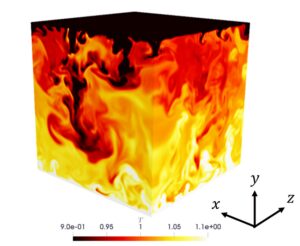
自然対流は、ある条件を得るために強制的な流れの付与によって強化されることがよくあります。この場合、浮力は依然として存在しますが、支配的ではありません。図4は、劇場空間の空調によって引き起こされる自然対流を示しています。エアコンは空間の上部に冷たい空気を送り込み、その空気は空間の下部にある暖かい空気の上向きの浮力によって下向きに流れます。このように、冷たい空気は下降流を形成し、再循環パターンは下図のようになります。
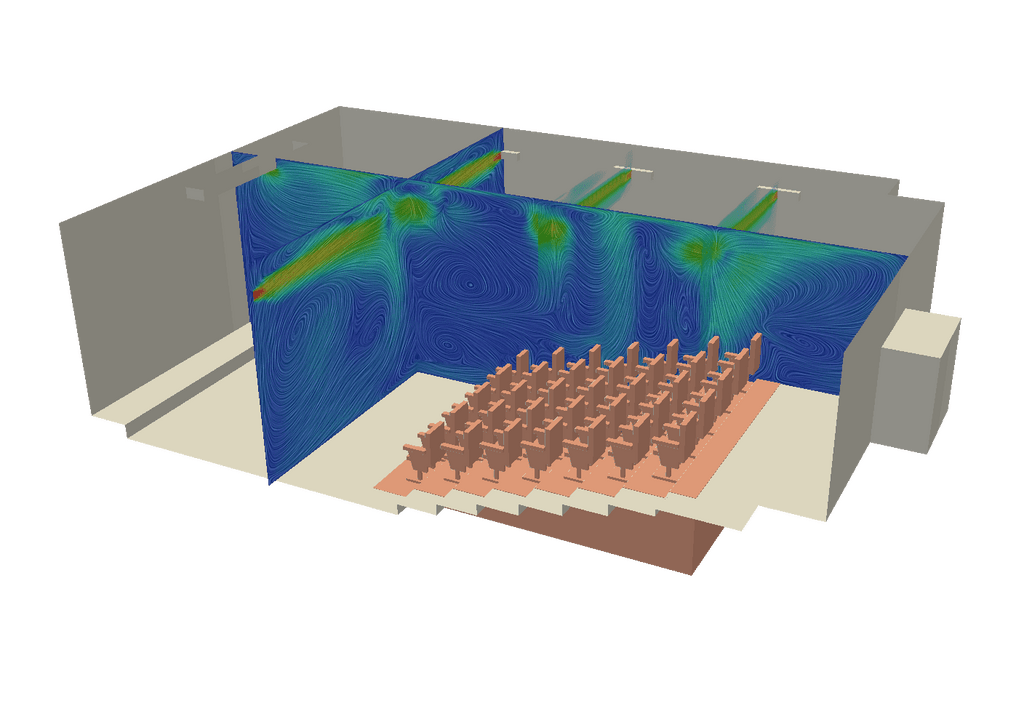
混相流における浮力効果
自然対流とは異なり、混相流における密度の変化は、温度の違いではなく、物質の状態の違いによるものです。流体力学に限って言えば、液体中の気体挙動、または、気体中の液体挙動の2つの可能性が最も一般的です。どちらの場合も、密度の高い相が下方に移動する傾向があります。
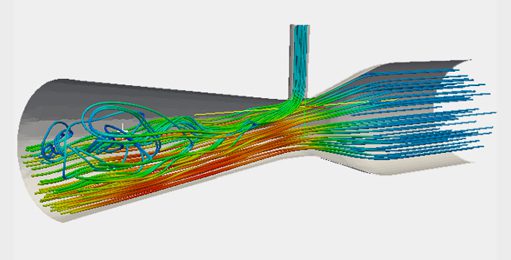
図5は、上昇する気泡の場合を示しています。気泡は周囲の液体よりも軽いため、浮力はその重さよりも強くなります。このアンバランスな力が慣性力に変わり、気泡の動的応答を引き起こします。
気泡は並進するだけでなく、変形していることに注意してください。これは、浮力だけが気泡に作用しているわけではなく、表面張力や粘性力も流れに影響しているためです。

SimScaleでは、自然対流を含む熱流体のシミュレーションや気液混相流のシミュレーションをウェブブラウザで実施いただけます。
浮力と合わせて読みたいページ
SimScale製品紹介資料ダウンロード

SimScaleの特徴と計算事例をまとめた資料を用意しております。