揚力係数とは、通常$C_L$ と表記され、物体の周囲を流れる流体の密度と速度、およびこの揚力が作用する表面積に対して、物体に発生する揚力を表したものです。これは無次元量であり、航空機の設計や製造、その他の分野でも非常に有用です。この記事では、揚力についてさらに詳しく説明し、なぜ揚力係数が重要なのか、そしてこれらの値を産業界で使用するためにどのように操作できるのかについて説明します。

揚力係数とは？

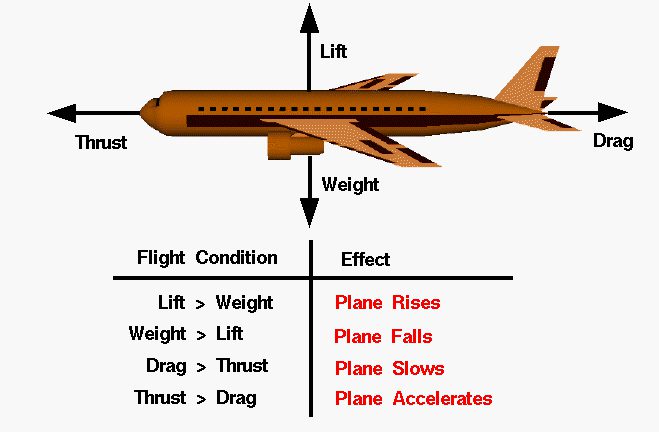
揚力係数とは何かという問いに答えるには、まず揚力とは何かを理解する必要があります。揚力とは、物体間の相対運動によって周囲の流体が物体に及ぼす力の垂直成分です。その名が示すように、揚力は通常、重力に抗して上方向に働きますが、技術的には流体の流れ方向に垂直などの方向にも働くことができます。通常、対象となる流体は空気ですが、液体媒体(水のような)でもかまいません。この記事では、デフォルトの流体として空気に焦点を絞ります。

図1: 流れる流体中の物体に作用する力[1]

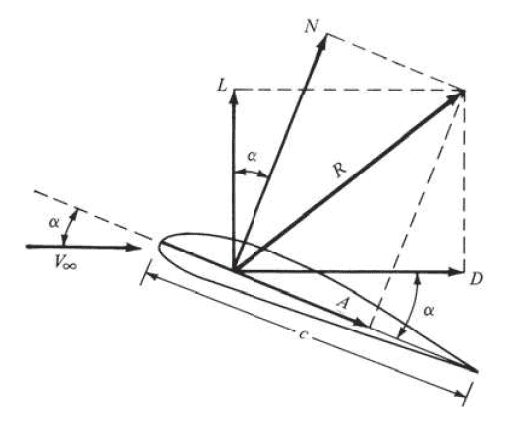
図 1 に示すように、揚力$L$ は、速度$V_∞$ (自由流速とも呼ばれる)で流れる流体によって及ぼされる空力力$R$ の成分です。力のうち、自由流速の方向に平行な成分$R$ は抗力$D$ として知られています。$A$ は軸力と呼ばれ、身体の長さに平行な$R$ の成分$c$ です。一方、$N$ は法線力と呼ばれ、$c$ に垂直な$R$ の成分です。

揚力係数を計算するための重要な方程式

揚力係数$C_L$は

$$ C_L = \frac{L}{qS} $$

または

$$ C_L = \frac{2L}{\rho U^2 S} $$

と表されます。ここで、

$L$は揚力(または揚力)

$S$は物体の基準表面積

$q$は動圧

$\rho$は流体の密度

$U$は流体の速度

です。

揚力係数は式中の次元が相殺されるため無次元です。これは物体とその形状の特性であり、ある流体の速度と密度からどれだけの揚力を発生させることができるかを示しています。物体が揚力を最大化し、抗力を最小化するようにうまく製造されている場合、この物体は翼、翼形、翼、または翼型と呼ばれます[2]。

翼型の断面は、図 2 に示すように、形状のすべての寸法と特性を定義するために代表的な長さをこのように呼ぶことが多いです。

図2: 翼の断面[1]

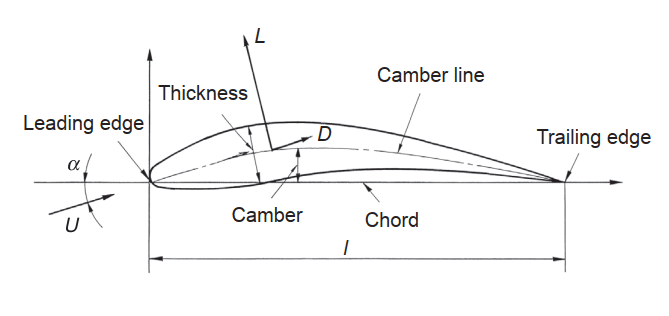
弦（Chord）は翼の前縁と後縁を結ぶ直線で、キャンバー線（Camber line）は翼の中央を通るこの2点を結ぶ曲線です。キャンバー線の最高点の弦からの高さをキャンバー（Camber）と呼びます。翼型の厚さ（Thickness）は、キャンバー線に垂直に測ったときの最大長です。流体の流れ方向($U$ )と弦の間の角度($\alpha$ )を迎え角と呼びます。

翼の幅を$b$ とし、その表面積を$A$ とすると、式$b^2/A$ はアスペクト比と呼ばれます。弦の長さを$l$ とすると、翼形の面積$A$ は$b \times l$ と表すことができるので、アスペクト比は$b^2/A$ または$b/l$ と書き換えることができます。

三次元の流れの研究は非常に複雑であることが多く、理論を単純化するために、通常、翼の二次元断面が採用されます。この断面では、揚力係数を断面揚力係数と呼ばれるものに分解することができます$c_l$ 。翼のスパンは無限であると仮定され、もはや変数ではありません。そこで、式は表面積を弦長に置き換えて$c_l$ を次のように与えます:

$$ c_l = \frac{L}{ql} $$ または$$ c_l = \frac{2L}{\rho U^2 l} $$

揚力係数と抗力係数の違い

揚力係数と抗力係数は本質的に同じものですが、一つ重要な違いがあります。

抗力係数$C_D$ は次のように表されます:

$$ C_D = \frac{D}{qS} $$ または$$ C_D = \frac{2D}{\rho U^2 S} $$

ここで、$D$ は抗力であり、他のパラメータは上記と同じです。

同様に、断面抗力係数$c_d$ は次式で与えられます:

$$ c_d = \frac{D}{ql} $$ または$$ c_d = \frac{2D}{\rho U^2 l} $$

揚力係数と抗力係数に加えて、モーメント係数と呼ばれる注目すべき係数があります。物体にかかる揚力と抗力は、重心と同様の意味で考えることができる圧力中心と呼ばれる仮想点に作用します。この圧力中心は、迎え角が変わると翼に沿って変化します。このような計算上の不都合な変化を避けるため、翼形上では従来、前縁から弦長の4分の1($l$ )の位置に固定点が選ばれており、この点を4分の1弦と呼んでいます。圧力中心を1/4弦に移動すると、力の平衡を得るためにその点でのモーメントを加える必要があります。

モーメント係数$C_M$ は次の式で表されます:

$$ C_M = \frac{M}{qSl_{1/4}} $$ または$$ C_M = \frac{2M}{\rho U^2 S l_{1/4}} $$

ここで、$M$ はモーメント、$l_{1/4}$ はクォーターコードです。

同様に、断面モーメント係数$c_m$ は次式で与えられます:

$$ c_m = \frac{M}{ql_{1/4}^2} $$ または$$ c_m = \frac{2M}{\rho U^2 l_{1/4}^2} $$

揚力係数の応用

揚力係数について学んだとき、「なぜ揚力係数が重要なのか」という当然の疑問が浮かびます。航空機の設計と製造において、空気抵抗成分に対する揚力成分を可能な限り増加させることが重要な目的のひとつです。同様に、電気風車、タービン、ボートのプロペラ、ヘリコプターのプロペラも、その効率を最大化するために、この情報をもとに製造されます。揚力係数は通常、迎角に対してプロットされ、揚力を最大化し、より効率的な機械、航空機、乗り物を製造するために、ある一定の条件下での翼形断面の挙動を知ることができます。グラフ上のこれらのプロットは、以下の図3に示すように、翼形特性曲線と呼ばれます。

図3: 揚力係数対迎角[2]

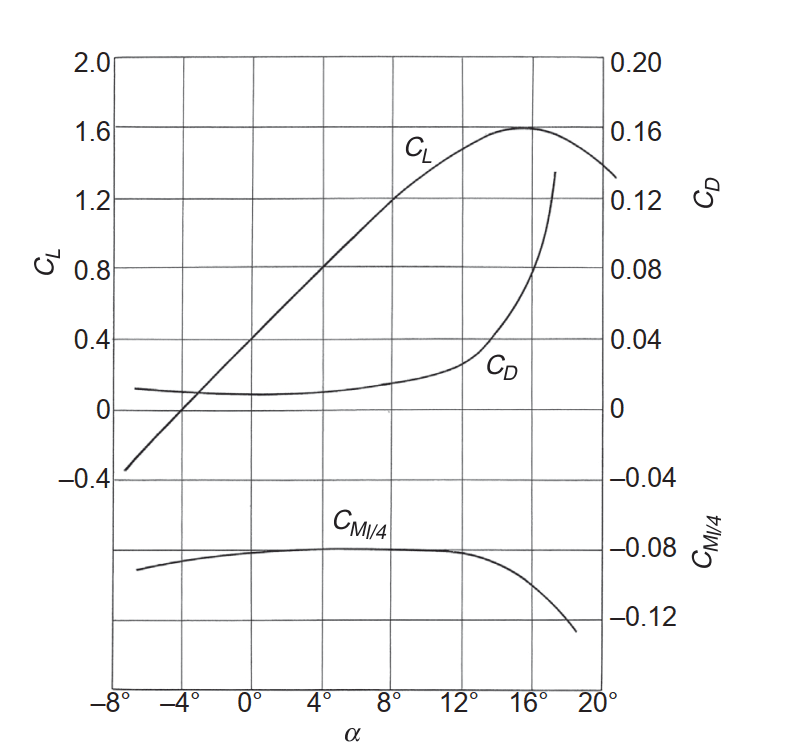
このグラフを見てすぐに分かることがいくつかあります。揚力係数は、迎角の増加とともに着実に上昇し、最大に達した後、下降に転じます。この時点で、翼型は失速すると言われています。揚力係数が最大になる角度を失速角、揚力係数がゼロになる角度をゼロリフト角と呼びます。

図3の例では1.6が最大値で、固定翼の最大値です。しかし、回転シリンダーのようないくつかの設計では、9を超える揚力係数を達成することができます[3]。

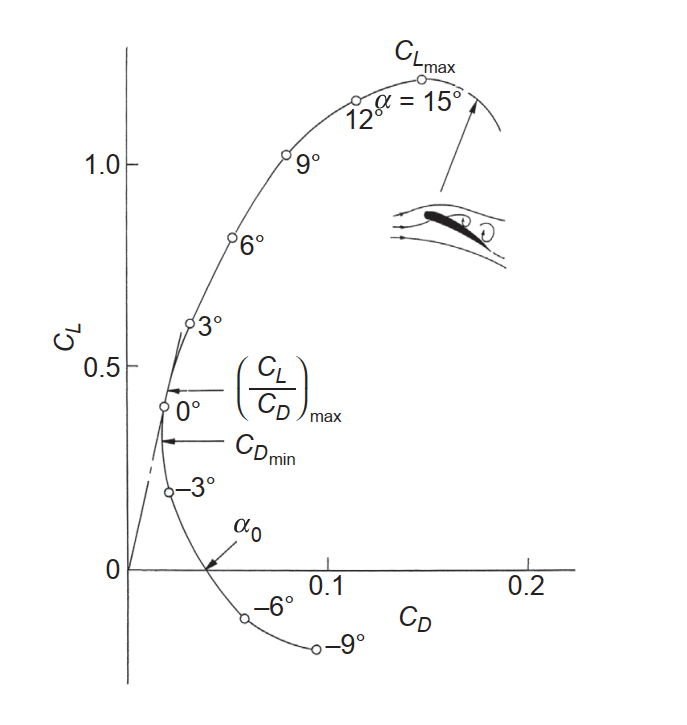
揚力係数と抗力係数は、図4に示すように、互いに対してプロットすることもできます。ここから、揚抗比($C_L/C_D)_{max}$を最大にする迎角を決定することができます。

図4: 揚力係数対抗力係数[2]

揚力係数を用いたシミュレーション

揚力、抗力、およびそれぞれの係数の値は、通常、試験対象の機体の縮小モデルを使用して風洞で経験的に決定されます。これは、特に多くの要素を考慮する必要がある非常に複雑な設計の場合であり、単純に物理的な試験を行う方が簡単であることがよくあります。しかし、風速やボディの大きさなど、現実の条件をすべて満たそうとすると、これは非常に高価な事業となります。

特定の要件を満たすために微調整や変更を行うには、確立されたベースデータを使用して計算流体力学(CFD)シミュレーションを行うことで、これらのテストを合理的な精度で実施することができます。このような基本データを入力し、他のデータを変化させることで、翼の挙動を研究・解析し、さらなる空力データを生成するのが一般的です。これにより、エンジニアは、幅広い条件下での設計の再現性と信頼性に関する必要な情報を得ることができます[4]。

図5: 揚力を発生させる圧力分布の違いを明らかにする翼形上の圧力の可視化

アニメーション1: 下部圧力がある上側の流れの加速を示す流速線

参考

Anderson, John. “Fundamentals of Aerodynamics.” McGraw Hill (2017): 19 – 26.
Nakayama, Yasuki. “Introduction to fluid mechanics.” Butterworth-Heinemann (2018): 177 – 200
Burgers, Phillip, and David E. Alexander. “Normalized lift: An energy interpretation of the lift coefficient simplifies comparisons of the lifting ability of rotating and flapping surfaces.” Plos one 7.5 (2012): e36732.
AeroToolbox, “Aerodynamic Lift, Drag and Moment Coefficients” https://aerotoolbox.com/lift-drag-moment-coefficient (accessed July 26, 2023)

2024年3月13日