Q値(第二不変量)について
(以下では、やや複雑な理論を紹介しますが、設定自体は簡単です！)
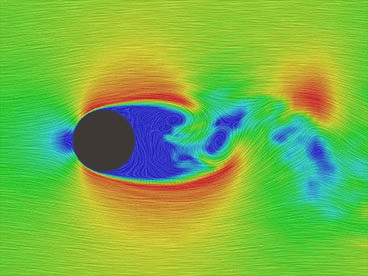
流体力学で用いられるパラメータのQ値(第二不変量)は、流れの渦の強さを評価する指標の一つです。特に、渦の構造を視覚的に捉えるために使われます。(学会などで見かけるかっこいいCFDの画像は、だいたいQ値です。)
流体の運動は変形(せん断や伸縮)と回転(渦)に分けられます。Q値は変形と回転の強さのバランスを評価することで、流れの中で、渦の影響が支配的か、変形の影響が支配的かを示します。
流れ場における速度勾配テンソル\(\nabla u\)を対称部分(変形テンソル\(S\))と反対称部分(渦度テンソル\(\Omega\))に分解できます。
\[\nabla u = S+\Omega\]
このQ値(第二不変量)は、対象部分(変形テンソル\(S\))と反対象部分(渦度テンソル\(\Omega\))から、以下のように定義されます。
\[Q=\frac{1}{2}(||\Omega||^2-||S||^2)\]
このＱ値は以下のことを表します。
\[\begin{equation} \begin{cases} Q>0: 渦の影響が強い\\ Q<0: 変形の影響が強い\end{cases} \end{equation}\]
CFDでQ値は渦の可視化に活用されます。例えば、飛行機周りの右図や、攪拌槽内の流れの解析で利用されます。Q値を等値面(等高線の3D版のようなもの)としてプロットすると、渦構造を可視化することができます。
ParaViewについて
ParaViewは、数値シミュレーションの結果を3Dで可視化するハイエンドの3D可視化ソフトウェアです。オープンソースで無料で利用でき、多くの機能を有しているため、研究機関や産業用途など幅広い分野で、高度な可視化処理に用いられます。
(解析を実施したSimScaleでも基本的なポスト処理を行うことができます。ParaViewを用いることで、より高度なポスト処理を行うことができます。)
1. 解析データの準備
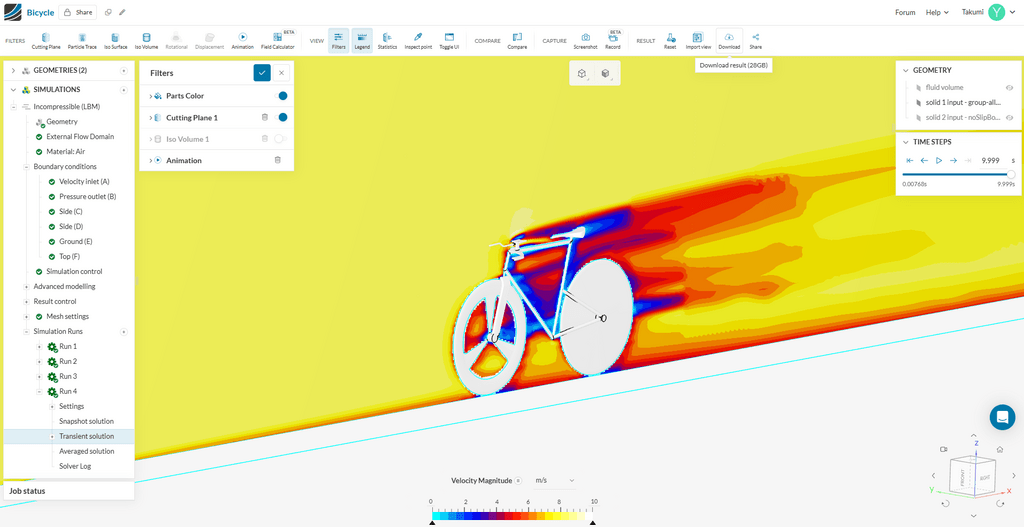
今回はSimScaleのIncompressible LBM (格子ボルツマン法)で、乱流を精緻に計算するロードバイク空力の非定常LES解析を行いました。ParaViewで処理を行うために、ローカル環境へダウンロードします。
格子ボルツマン法は近年実用化が進む新しい解法で、大規模非定常LESを高速に計算することを可能にします。今回は、138万メッシュ、1,300時間ステップの大規模な計算が60分で完了しました！格子ボルツマン法について詳しくは、以下のページをご覧ください。
格子ボルツマン法とは
格子ボルツマン法(LBM)は計算流体力学(CFD)手法の1つです。 LBMは、複雑な流れシナリオや複雑な形状を扱うことができるため、その応用範囲は大きく広がっています。航空宇…
2. ParaViewでQ値の計算と可視化
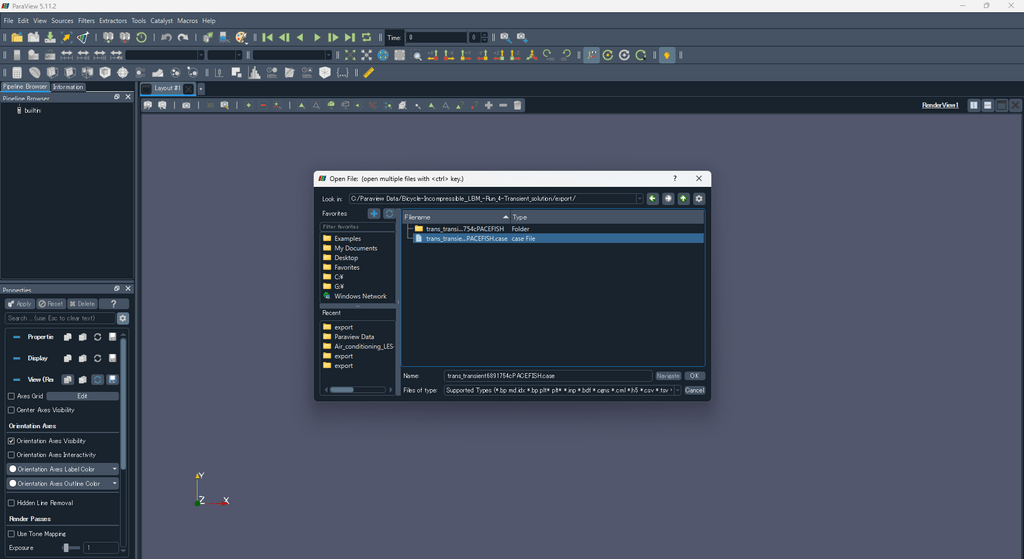
ダウンロードしたデータ(.case)をParaViewで開きます。File -> Open
GradientフィルターでQ値の計算を行います。Filters -> Alphabetical -> Gradient
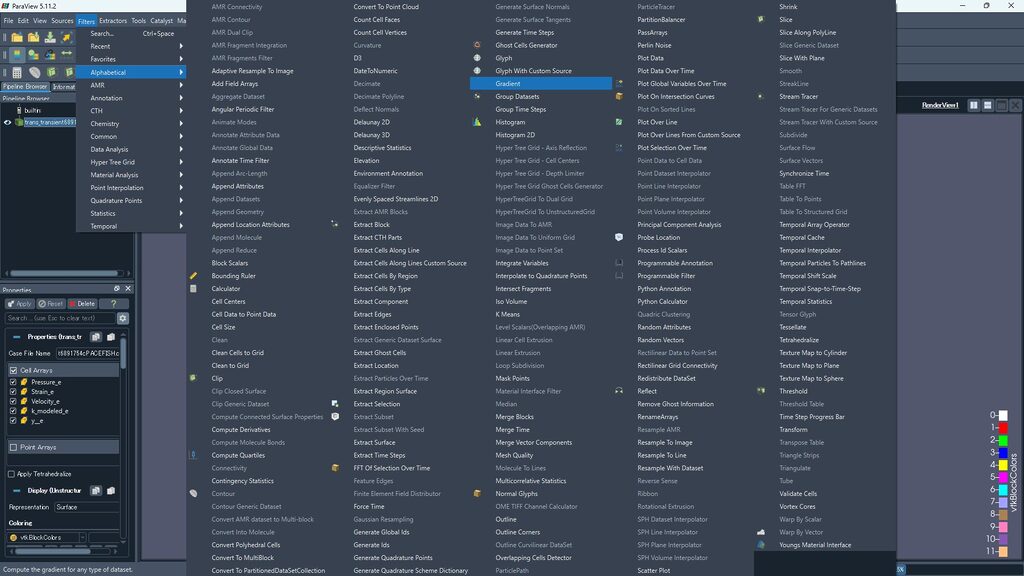
その後、PropertiesでCompute Q-criterionにチェックを入れるだけです！同様に発散(Divergence)と渦度(Vorticity)も計算できます。
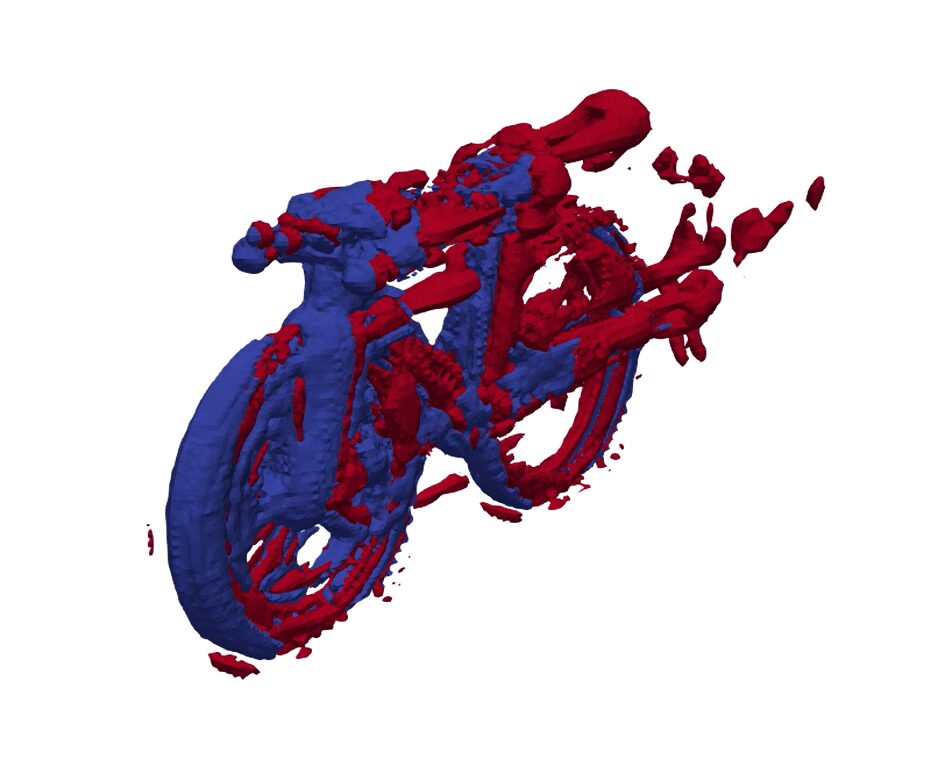
以下のアニメーションは、Q値の正(赤)と負(青)で等値面を表示し、アニメーションにしたものです。もくもくと渦構造が発生し、後流へ流れていく様子を確認できます。
SimScaleはWebアプリとして提供されており、シミュレーション用のハードウェア不要でハイスペックな解析を実施できます。以下のページより無料でアカウント作成するとすぐに解析をお試しいただけます。
(今回の事例で実施したIncompressible LBMソルバーは無料プランではお使いいただけませんが、無料プランでお使いいただける有限体積法ソルバーの結果をParaViewで可視化することも可能です。)