メッシュとは何か?なぜ必要なのか?基礎から学べるシミュレーション入門。図解とともにメッシュ生成の考え方をやさしく説明します。
メッシュとは、有限要素解析 (FEA) や数値流体解析 (CFD) におけるシミュレーションプロセスの基本要素の1つです。セルと点(またはノード)で構成されるネットワークであり、ほぼどんな形状や大きさにもすることができます。
このメッシュは偏微分方程式 (PDE) を解くために使用されます。メッシュの各セルは方程式の個別の解を表しており、それらのネットワーク全体として組み合わせることで、全体の解が得られます。
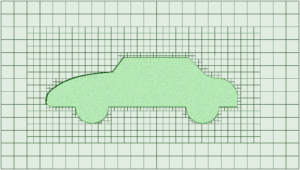
CAEにおけるメッシュは、画像に例えると画素 (ピクセル) に相当します。
メッシュが粗いほど形状の再現性は低下し、細かくするほどより正確に形状を再現できます。一方で、メッシュを細かくしすぎると計算コストが増大するため、精度と計算負荷のバランスを考慮したメッシュサイズの設定が重要です。
物体全体を小さな要素に分割せずに一度に解こうとすると、その形状の複雑さのために不可能な場合があります。
穴や角、複雑な形状はソルバーが解を求めるの極めて困難にします。一方で、小さなセルは比較的容易に解くことができるため、より好ましい戦略とされています。
メッシュ生成 (メッシング) とは?
メッシュ生成 (メッシング) とは、形状の上に2次元または3次元のグリッドを生成し、それを離散化してシミュレーションで解析可能にする手法を指します。このグリッド (メッシュ) は、会場の複雑さに応じて定義されます。
メッシュ技術の歴史的背景
メッシュおよびメッシング技術の歴史は、数値解析手法の発展と密接に関係しています。
Courant, Friedrichs, Lewy による論文は、有限差分法 (FDM) の基礎を築いた画期的な研究とされており、ここでクーラン条件 (CFL:
Courant–Friedrichs–Lewy 安定条件)といった概念が導入されました。
メッシュ形状と解析手法の関係
歴史的に、矩形格子や直交格子 (Cartesian grid) は有限差分法と結びついており、これは隣接するセルやノードの値を利用して変数の挙動を近似する仕組みに基づいています。
一方、有限要素法 (FEM) の登場によって、混合形状のメッシュセルが扱えるようになり、非構造格子 (非構造メッシュ) が現実的な選択肢となりました。
変分法への起源
数値的に問題を解くための変分法的アプローチの起源は、19世紀から20世紀初頭にかけての Lord Rayleigh および Ritz の研究にまで遡ります。これらの研究が、今日の有限要素法の理論的な礎を築いたと言えます2。
メッシュ離散化
偏微分方程式 (PDE) の集合を数値的に解くための最初のステップは、①方程式の離散化と、②領域の離散化 です。
先に述べたように、領域全体を一度に解くことは不可能ですが、それを小さな部分に分割して複数同時に解くことは可能です。
①方程式の離散化
このプロセスは、有限差分法 (FDM)、有限体積法 (FVM)、有限要素法 (FEM) といった手法に関連しています。
これらの手法の目的は、連続的な形で表現された方程式を、代数的な差分方程式の体系に変換することです。
つまり、連続領域で定義されている物理現象を、計算可能な数値モデルへと変換します。
②領域の離散化
一方、領域の離散化では、解析対象の空間を離散的なセルやノードの集合として表現します。
これにより、もともと連続的だった物理空間を有限個の要素 (セル) で覆うことができ、各セルで物理方程式を解くことで、全体の解を組み立てることが可能になります。
要するに、
- 方程式の離散化 → 数学的モデルを計算可能な形に変える
- 領域の離散化 → 幾何学的領域を計算可能な形に分割する
という、2つの離散化が、数値解析の基礎を構成しています。

メッシュとは、定義上、点とセルが接続されて構成されたネットワークのことを指します。
このネットワークは、さまざまな幾何形状やトポロジー (接続構造) を持つことができます。
メッシュはしばしば「グリッド (格子)」とも呼ばれますが、これはメッシュの内部的な構造の規則性や、特に有限差分法 (FDM) に関連する場合に用いられる呼び方です。
メッシュの各セルまたはノードには、離散化の方法に応じて局所的な方程式の解が割り当てられます。
つまり、方程式がセル上で離散化されているか、ノード上で離散化されるかによって扱いが異なり、これは解析プロジェクトの方針 (設計判断) によって決まります。
一般的に、点離散化 (Point discretization) は有限差分法 (FDM) を用いる場合に採用されます。
この方法では、偏微分方程式 (PDE) は各点の近接点におけるテイラー展開によって近似されます。
場合によっては、点離散化が有限体積法 (FVM) と組み合わせて用いられることもありますが、その場合でも点の周囲に仮想的なセルを設定する必要があります。
一方で、離散化される方程式が弱形式 (Week form)、積分形式 (Integral form)、または保存形式 (Conservative form) で表される場合、離散化されたセル上で積分を解くのが一般的です。
例えば、輸送現象 (Transport phenomena) を扱う場合、有限体積法では、各セルを小さな体積要素 (コントロールボリューム) として表現します。
そのうえで、セルを通過するフラックス (流束) のバランスをとり、各セル内では解が一定であると仮定して解析を行います。
メッシュの種類
メッシュは一般的に、構造格子 (構造メッシュ) と非構造格子 (非構造メッシュ) に分類されます。
先に述べたように、構造格子は歴史的に有限差分法 (FDM) と深く関連しています。
一方、有限体積法 (FVM) や有限要素法 (FEM) では、より汎用的な形状のメッシュを扱うことができます。
構造格子 (構造メッシュ)
構造格子 (構造メッシュ) は、規則的は構造と配置を持ち、隣接するセルや点を容易に識別できるという特徴を持ちます。
この性質は、構造格子が解析的な座標系 (直交座標系、楕円座標系、球座標系など) 上に適用されることから生まれ、結果として規則的なグリッドを形成します。
プログラム的な観点から見ると、構造格子や構成するセルやノードは規則的に規則的に番号付けすることが可能です。
これにより、隣接セルの検索をセル番号の単純な演算で求められるという利点があります。
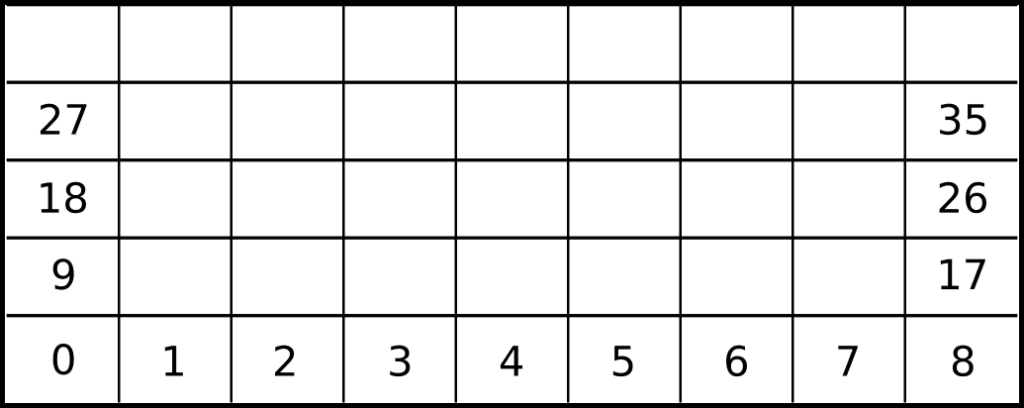
例えば、下図のような矩形メッシュを考えてみましょう。
最初の数個のセルおよび左右境界上の最初の4セルが番号付きで示されています。
このメッシュは典型的な矩形格子の例です。
- 右隣のセルを求めたい場合:
そのセル番号に+1するだけで右隣を特定できる。 - 上隣のセルを求めたい場合:
そのセル番号に+9するだけで上隣が特定できる。
このように、各セルを配列やベクトルのインデックスとして直接対応づけられるため、計算処理が非常に容易になるのが構造格子の大きな利点です。
任意の曲座標格子も、このような座標系および隣接関係の体型に写像することができます。
したがって、プログラム上の観点から見ると、隣接セルの検索という点において、曲線格子と矩形格子の間にはほとんど違いがないといえます。
構造格子 (構造メッシュ) は、境界への適合という観点から定義されることもあります。
例えば、直行格子 (Cartesian grid) は矩形領域の境界に適合し、円柱座標格子 (Cylindrical grid) は円柱形状の境界に適合します。
さらに、複数の境界適合の考え方を組み合わせることも可能です。
これにより、異なる形状の曲線や曲面を境界として定義することができます。
こうした境界には、スプラインやNURBS (Non-Uniform Rational Basis Spline) といったパラメトリックに定義可能な曲線・曲面が含まれます。

非構造格子 (非構造メッシュ)
非構造格子は、より汎用的であり、任意の形状のジオメトリを近似的に表現できるという特徴を持ちます。
構造格子とは異なり、非構造格子ではセルやノードの配置が規則的な行列構造に対応しません。
そのため、座標や接続関係をとくべつデータ構造で管理する必要があります。
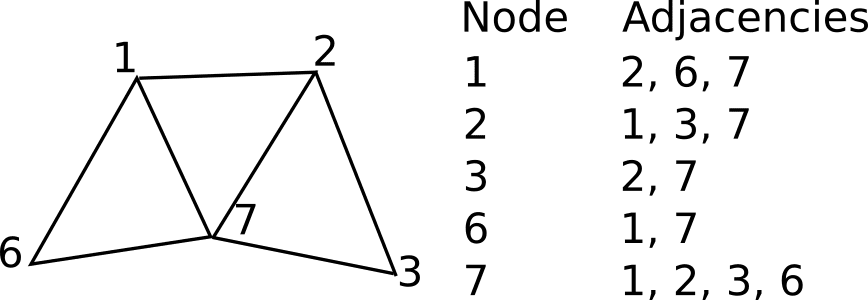
プログラム上では、非構造格子では以下のようなデータ管理が行われます:
- 隣接関係行列 (Adjacency matrix)または隣接リスト (Adjacency list)
- ノード座標リスト (Node coordinates list)
これらの構造によって、どのセルやノードがどの要素と接続しているかを保持します。
また、非構造格子ではノードやセルの番号付け (node/cell numbering) が任意かつ疎であることが一般的です。
これは、解析的な隣接関係の式 (Analytical adjacency query) を必要としないためで、より自由なメッシュ生成と複雑な形状の再現を可能にしています。
複雑なジオメトリ形状で、構造格子を生成するのが現実的でない場合には、非構造メッシュ手法を用いて離散化を行うことができます。
非構造メッシュは柔軟性が高く、様々な種類のセル (要素) を同一メッシュ内で共存させることが可能です。
これにより、ジオメトリ形状への適合性がさらに向上し、全体としての要素品質も改善されます。
セル (要素) の種類
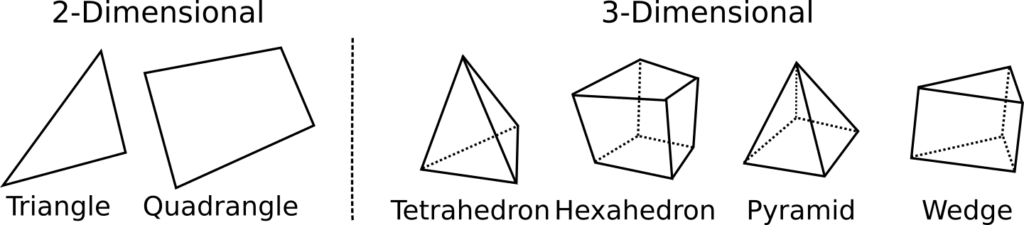
セルの種類には大きく分けて2次元要素 (2D) と3次元要素 (3D) に分類されます。
- 2次元セルの代表例
- 三角形 (Triangle)
- 四角形 (Quadrangle)
- 3次元セルの代表例
- 四面体/テトラ (Tetrahedron)
- 六面体/ヘキサ (Hexahedron)
- ピラミッド (Pylamid)
- プリズム (Wedge)
これらの要素タイプは、しばしばFinite element zoo (直訳: 有限要素動物園) と呼ばれます。これは、有限要素法 (FEM) でこれら多様な要素が使われてきた歴史を反映した言葉です。
一方、有限体積法 (FVM) はより柔軟で、使用するセルの形状に制約が少なく、多角形 (Polygon) や多面体 (Polyhedron) といった、ほぼ任意形状を扱うことが可能です。
メッシュセルは必ずしも整合している必要はありません。非整合メッシュとは、「ハンギングノード (ぶら下がり接点)」が存在するメッシュのことを指します。これらのノードは、メッシュの適応 (アダプテーション) 処理の過程でより一般的に現れます。
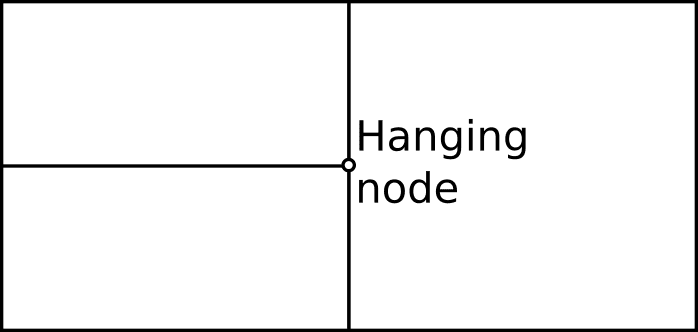
メッシュのアダプション (適応化)
非構造メッシュでは、点や隣接関係が特定の規則的構造に従わないため、メッシュセルやノード (点) を追加・削除することが可能です。
このように、解析の進行中にメッシュセルや点を動的に追加・削除・移動させる処理をメッシュアダプション (適応化) と呼びます。
メッシュアダプションの目的
解析対象によっては、解の精度を高めつつ計算コストを抑えるために、メッシュアダプションの手法が必要になります。
つまり、全体のセル・ノード数を制御しながら、誤差の大きい領域のみを局所的に細分化 (リファインメント) することで、精度と効率のバランスを取るのです。
一般的に、必要な細分化の度合は誤差に関連しており、解くべき方程式に基づいてその誤差を推定します。
そのため、誤差が大きい領域ほどセルが密集し、誤差の小さい領域ではセルが粗くなります。
メッシュリファインメント (細分化) の主な種類
メッシュのリファインメント (細分化) は、以下のような一般的なタイプに分類されます:
- h型リファインメント (メッシュリファインメント)
- r型リファインメント (メッシュ移動)
- p型リファインメント
- デリファインメント
- 上記の組み合わせ
このようなメッシュ適応技術は、流体解析、構造解析、熱伝導解析など、多くの分野で効率的な高精度解析を実現する重要なアプローチです。
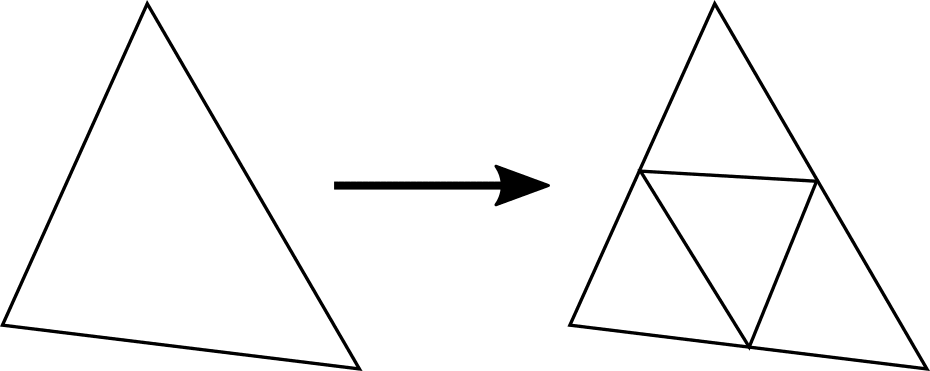
h型リファインメント (メッシュリファインメント)
h型リファインメント (または、メッシュリファインメント) とは、セルや点を追加することで、局所的な代表長さを短くし、解像度を高める手法です。
この方法は、局所的なメッシュ分解能を比較的低コストで向上させることができますが、同時に自由度が増加するため、連立方程式の数が増え、計算コストも上昇します。
非構造格子での細分化
非構造格子では、セルやノードの追加は比較的容易です。
これは、セルの接続関係を再構築するだけで済むため、複雑なジオメトリでも柔軟に適用できます。
構造格子での細分化
一方、構造格子では、セルを追加すると格子の規則性を損なう可能性があるため、細分化はそれほど単純ではありません。
そのため、適応構造格子 (Adaptive structured grids) を使用する場合は、しばしば非整合メッシュ (Nonconforming mesh) を許容して処理を行います。

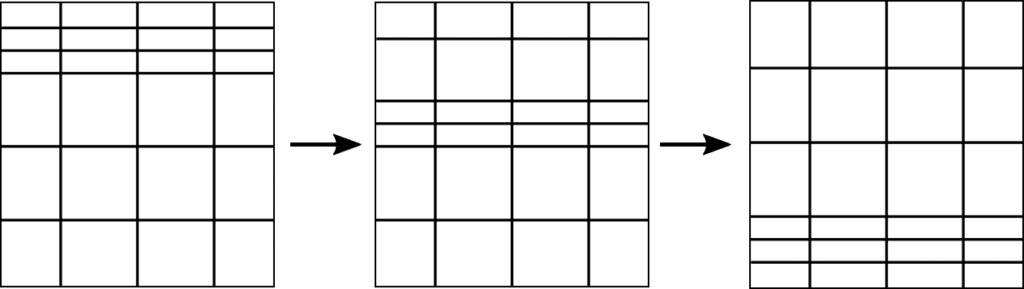
同様に、メッシュリファインメント (細分化) の手法には、一般的にメッシュデリファインメント (粗化) も含まれます。
これは推定誤差が非常に小さい領域のセル数を減らすために用いられる手法です。
この処理により、計算資源をより効率的に活用でき、計算コストやシミュレーション時間の削減が可能になります。
r型リファインメント (メッシュ移動)
r型リファインメント (またはメッシュ移動) とは、メッシュのセルや点を移動・変位させることで解像度を調整する手法です。
この場合、セルや点の数は変わらず、場合によっては接続関係 (Connectivity) も維持されます。
例えば図11のように、衝撃波伝搬の問題を扱う際、解の変化が大きい領域にメッシュを集中配置することで、セル数を増やさずに局所的な解像度を高めることができます。
その他のメッシュアダプション
他の代表的なメッシュ適応化手法として、p型リファインメントとアダプティブメッシュがあります。
p型リファインメント
これは有限要素法 (FEM) に関連する手法で、メッシュ構造を変えずに要素内の形状関数の次数を上げることで精度を向上させます。
つまり、セル数は増えずに「式の表現力」を高めるアプローチです。
アダプティブメッシュ
推定誤差に基づいて新しいメッシュを再生成する手法です。
これにより、高いメッシュ品質を保ちながら必要最低限の点数で解析を行うことができます。
ただし、メッシュ生成のオーバーヘッド (計算負荷) が大きくなる場合があります。
この方法は、誤差が高い/低い領域のみを局所的にリメッシュする形でも利用可能です。
アニメーション1: アダプティブメッシュの例。流れの特性に応じて、必要な細分化レベルに合わせてセルが動的に生成・削除されます。
手法の組み合わせ
これらの手法を組み合わせることも可能です。
例えば、r型+h型リファインメントを組み合わせたものはrh型リファインメントと呼ばれ、メッシュ上でノードの移動と新規生成生成の両方を行うことができます。
SimScaleにおけるメッシング
SimScaleでは、多様なメッシングアルゴリズムとメッシュタイプが用意されています。
これにより、解析の種類やジオメトリの複雑さに応じて、最適なメッシュを自動または手動で生成できます。

プラットフォームでよく見られる例の一つが、内部流れ解析のためのパイプのメッシングです。
図13では、テトラメッシュ優勢でメッシュを作成する様子を示しています。

数ある優れた機能の中でも、SimScaleはHex-dominantメッシングアルゴリズムにおいて、snappy-HexMesh機能を採用しています。
この機能により、ヘキサ要素および分割ヘキサ要素で構成された3次元のハイブリッドメッシュを自動的に生成することができます。
参考
- Courant, R., Friedrichs, K.O., Lewy, H., “Über die partiellen Differenzengleichungen der Mathematischen Physik”, 1928
- Thomée, V., “From finite differences to finite elements: A short history of numerical analysis of partial differential equations”, 2001
- Thompson, J. F., Soni, B. K., Wheatherill, N. P., “Handbook of Grid Generation”, 1999
メッシュと合わせて読みたい
SimScale製品紹介資料ダウンロード

SimScaleの特徴と計算事例をまとめた資料を用意しております。