対流とは、温度に応じて固体から流体へ、またはその逆に熱が移動することです。この熱の移動は、流体の移動によってもたらされます。流れが速ければ速いほど、熱伝達量は多くなります。加えて、熱伝達量は固体と流体間の温度差にも依存します。対流の性質が複雑であるにもかかわらず、従来のニュートンの加熱/冷却の法則を用いて次のように表現できます:
$$Q=hA_s\left(T_0-T_\infty\right)$$
ここで \(h\) は対流熱伝達率であり、\(A_s\)は表面積です。ここで問題となるのは熱伝達率の解析式です。係数は単純に見えますが、実はそうではありません。熱伝達率には多くの物理現象が含まれています。従って、熱伝達係数は熱に関する多くのパラメータに依存します。対流係数の値に影響を与えるパラメーターのうち、代表的なものは以下の通りです:
- 表面形状
- 流体運動
- 流体の物性値
対流は、流体がファン、ポンプ、または風のような外部ソースによって動かされ、流体速度がほぼ一定である場合に強制されることがあります。これを強制対流と呼びます。
強制対流
対流熱伝達率のスケール解析
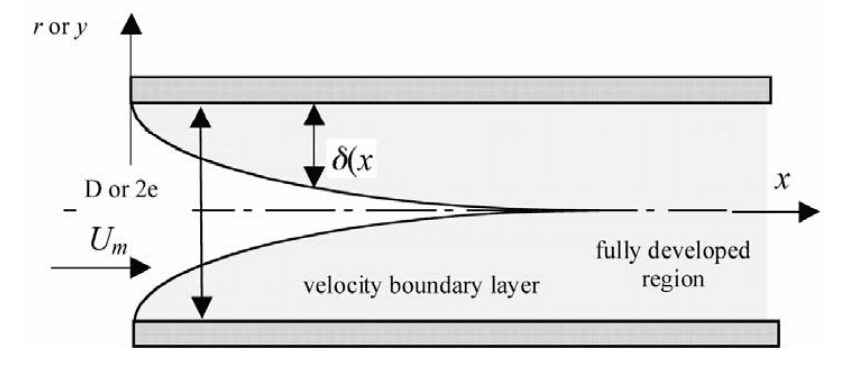
ご存知のように、流体が平衡状態の固体表面上を流れるとき、必ず境界層が形成されます。境界層は運動量の小さい流体領域です。\(y→0\)における固体境界のごく近傍の流速は0であり、基本的に流体は固体表面に接触して静止しています。流速は固体表面から離れるにつれて徐々に増加し、最終的には流速に一致します。
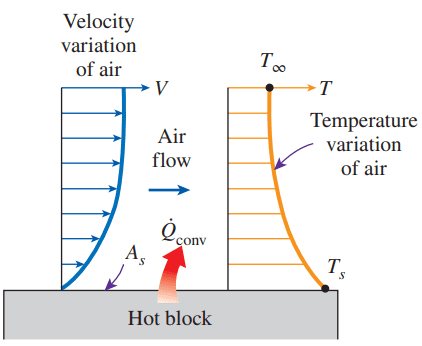
\(y → 0\) では流体は動いていないので、境界に近いところでは熱のやり取りは固体と流体間の熱伝導として起こります。
$$Q=-kA_s\left(\frac{\partial T}{\partial y}\right)_{y=0}$$
熱伝導と熱伝達を等式化すると、以下の式が得られます。
$$h=-\frac{k\left(\frac{\partial T}{\partial y}\right)_{y=0}}{\left(T_0-T_\infty\right)}$$
ここで\( k\)は熱伝導率です。
固体表面と流体間の全温度差は\(\left(T_0-T_\infty\right)=\Delta T\) となります。熱境界層の厚さは\(\delta_T\) と非常に小さく、全温度変化は\(\Delta T\) であるため、対流熱伝達率は次のように書くことができます:
$$h=-\frac{k\left(\frac{\Delta T}{\delta_T}\right)}{\Delta T}=\frac{-k}{\delta_T}$$
流れ場を定義するために、2次元流れ場を仮定した質量と運動量の保存方程式から始めることができます:
$$\frac{\partial u}{\partial x}+\frac{\partial v}{\partial y}=0$$
$$u \frac{\partial u}{\partial x} + v \frac{\partial u}{\partial y} = – \left(\frac{1}{\rho}\right) \left(\frac{\partial P}{\partial x}\right) + \nu \left(\frac{\partial^2 u}{\partial x^2} + \frac{\partial^2 u}{\partial y^2}\right)$$
$$u \frac{\partial v}{\partial x} + v \frac{\partial v}{\partial y} = – \left(\frac{1}{\rho}\right) \left(\frac{\partial P}{\partial y}\right) + \nu \left(\frac{\partial^2 v}{\partial x^2} + \frac{\partial^2 v}{\partial y^2}\right)$$
$$u \frac{\partial T}{\partial x} + v \frac{\partial T}{\partial y} = \alpha \left(\frac{\partial^2 T}{\partial x^2} + \frac{\partial^2 T}{\partial y^2}\right)$$
パラメータ:
- \(u =\): x方向の流体速度
- \(v =\): y方向の流体速度
- \(\nu =\): 動粘度
- \(\alpha=\): 熱拡散率
- \(k=\): 熱伝導率
連続の式と運動量の式から、次の関係式が得られます:
$$\frac{U_\infty}{L}=\frac{v}{\delta}$$
パラメータ:
- \(\delta=\): 境界層の厚さ
- \(L=\): 固体表面の長さ
- \(U_{\infty}=\): 自由流れ速度
- \(v=\): 表面に垂直な流れの速度
運動量方程式のさまざまな項を以下に示します。最初の2つは運動量の項、3つ目は圧力の項、最後の2つは流れの摩擦の項です。
$$\frac{{U_\infty}^2}{L},\frac{v U_\infty}{\delta},\frac{P}{\rho L},\nu \frac{U_\infty}{L^2}, \nu \frac{U_\infty}{\delta^2}$$
流れ摩擦項である第4項は、最後の項よりもはるかに小さく、どちらの運動量方程式でも無視できることが容易にわかります。したがって、\(\frac{\partial^2}{\partial x^2}\) を無視することができます。
同様に、\(x\)と\(y\)の運動量方程式の圧力項については、圧力勾配が摩擦項と釣り合う必要があります。したがって次式が得られます:
$$\left(\frac{1}{\rho}\right)\left(\frac{\partial P}{\partial x}\right)\sim \nu \frac{\partial^2 u}{\partial y^2} \text{ and } \left(\frac{1}{\rho}\right)\left(\frac{\partial P}{\partial y}\right)\sim \nu \frac{\partial^2 v}{\partial y^2}$$
$$\frac{\partial P}{\partial x} \sim \mu\frac{U_\infty}{L^2} \text{ and } \frac{\partial P}{\partial y} \sim \mu\frac{v}{\delta^2}$$
明らかに、yの圧力勾配はxの圧力勾配に比べて無視できるほど小さく、境界層内の圧力勾配はバルクフロー内の圧力勾配と同じになります。慣性の項と摩擦の項を等しくすると、次の関係が得られます:
$$\frac{{U_\infty}^2}{L} = \nu\frac{U_\infty}{\delta^2} \Rightarrow \delta = \left(\frac{\nu L}{U_\infty}\right)^\frac{1}{2} \Rightarrow \frac{\delta}{L} = {{Re}_L}^{-\frac{1}{2}}$$
ここで\(Re_L\)(レイノルズ数)\(=\frac{U_\infty}{\nu L}\)です。
同様に、エネルギー方程式から、以下の項が得られます:
$$\frac{U_\infty \Delta T}{L} , \frac{v\Delta T}{\delta_T} , \alpha\frac{\Delta T}{L^2} , \alpha\frac{\Delta T}{{\delta_T}^2}$$
ここでも第3項は第4項に比べて無視できるほど小さく、\(L\text{ >> }{\delta_T}^2\) となります。したがって、次の関係が得られます:
$$\frac{v\Delta T}{\delta_T} \sim \frac{U_\infty \Delta T}{L}\left(\frac{\delta}{\delta_T}\right)$$
熱境界層が速度境界層よりもはるかに厚い場合、すなわち\(\delta\text{ << }\delta_T\) の場合、エネルギー方程式の第2項は第1項と比較して小さくなり、無視することができます。式は次のようになります:
$$\frac{U_\infty \Delta T}{L} \sim \alpha\frac{\Delta T}{{\delta_T}^2} \Rightarrow \frac{\delta_T}{L} \sim {Pr}^{-\frac{1}{2}} {{Re}_L}^{-\frac{1}{2}} \Rightarrow \frac{\delta_T}{\delta} \sim Pr^{-\frac{1}{2}}$$
ここで\(Pr\)(プラントル数)\(=\frac{\nu}{\alpha}\)です。
上記の式から、\(\delta << \delta_T, Pr < 1\) (この範囲は一般に液体金属で示されます)ならば、対流熱伝達率は次のように書くことができると結論づけることができます:
ここで\(Nu\)(ヌセルト数)\(=\frac{hL}{k}\)です。
熱境界層が速度境界層より小さい場合\(\delta >> \delta_T\) 、\(u\)の項は\(U_\infty \frac{\delta_T}{\delta}\) となり、質量保存のため\(\frac{u}{L} = \frac{v}{\delta_T}\) となります。これらをすべて用いると、次の関係が導かれます:
$$\frac{\delta_T}{L} \sim {Pr}^{-\frac{1}{3}} {{Re}_L}^{-\frac{1}{2}} \Rightarrow \frac{\delta_T}{\delta} \sim {Pr}^{-\frac{1}{3}} \Rightarrow h \sim \frac{k}{L} {Pr}^{\frac{1}{3}} {{Re}_L}^{\frac{1}{2}} \Rightarrow \text{Nu} \sim {Pr}^{\frac{1}{3}} {{Re}_L}^{\frac{1}{2}}$$
\(\delta >> \delta_T\)から、\(Pr < 1\)であることがわかります。上記の関係はすべて、固体表面温度が一定である平板上の強制対流に対して有効です。
対流熱伝達率/ヌセルト数の様々な表現とは?
この節では、対流熱伝達係数/ヌセルト数について、解析計算の第一近似として用いることのできるいくつかの式を列挙します:
平坦な固体表面上の層流の熱伝達率
ヌセルト数の値は、それを導き出すために使用される解析手法によって異なる場合があります。最も一般的に使用される方法を使用すると、平均ヌセルト数は次のようになります。これらの結果はすべて、層流を持つ平坦な等温のプレート、すなわち\(Re < 5 (10^5)\) に対して有効です。
$$Nu = 1.128 {Pr}^\frac{1}{2} {{Re}_L}^\frac{1}{2} \text{for Pr } < 0.5$$
$$Nu = 0.664 {Pr}^\frac{1}{3} {{Re}_L}^\frac{1}{2} \text{for Pr } > 0.5$$
プラントル数の全範囲については、以下の式も使用できます:
$$Nu = \frac{0.928 {Pr}^\frac{1}{3} {{Re}_L}^\frac{1}{2}}{\left(1+\left(\frac{0.0207}{Pr}\right)^\frac{2}{3} \right)^\frac{1}{4}}$$
局所ヌセルト数は次のようになります:
$${Nu}_x = 0.564 {Pr}^\frac{1}{2} {{Re}_x}^\frac{1}{2} \text{for Pr } < 0.5$$
$${Nu}_x = 0.322 {Pr}^\frac{1}{3} {{Re}_x}^\frac{1}{2} \text{for Pr } > 0.5$$
非加熱開始部が\(x = x_0 \text{for Pr } > 0.5\)の平板では、次式が得られます。
$${Nu}_x = 0.322 {Pr}^\frac{1}{3} {{Re}_x}^\frac{1}{2} \left(1-\left(\frac{x_0}{x}\right)^\frac{3}{4}\right)^{-\frac{1}{3}}$$
壁面温度の代わりに壁面熱流束が一定の場合、\(10 > Pr > 0.5\) であれば、ヌセルト数の式は次のようになります:
$${Nu}_x = 0.453 {Pr}^\frac{1}{3} {{Re}_x}^\frac{1}{2}$$
ダクト内の層流完全発達強制流れに対する対流熱伝達
形状 |
熱条件 |
Nu |
| 円筒ダクト | 均一な壁面熱流束 | 4.36 |
| 円筒ダクト | 均一な壁面温度 | 3.66 |
| 平面流路 | 均一壁面熱流束 | 8.23 |
| 平面チャンネル | 均一壁面温度 | 7.54 |
ここで、レイノルズ数は水力直径に基づいて計算されます。水力直径は以下のように計算できます:
$$D_h = \frac{4S}{P}$$
ここで、各物理量は以下の通りです。
\(S=\) 断面積
\(P=\) 接液周囲長
一様で層流の異なる断面積のダクトのヌセルト数を以下に示します:
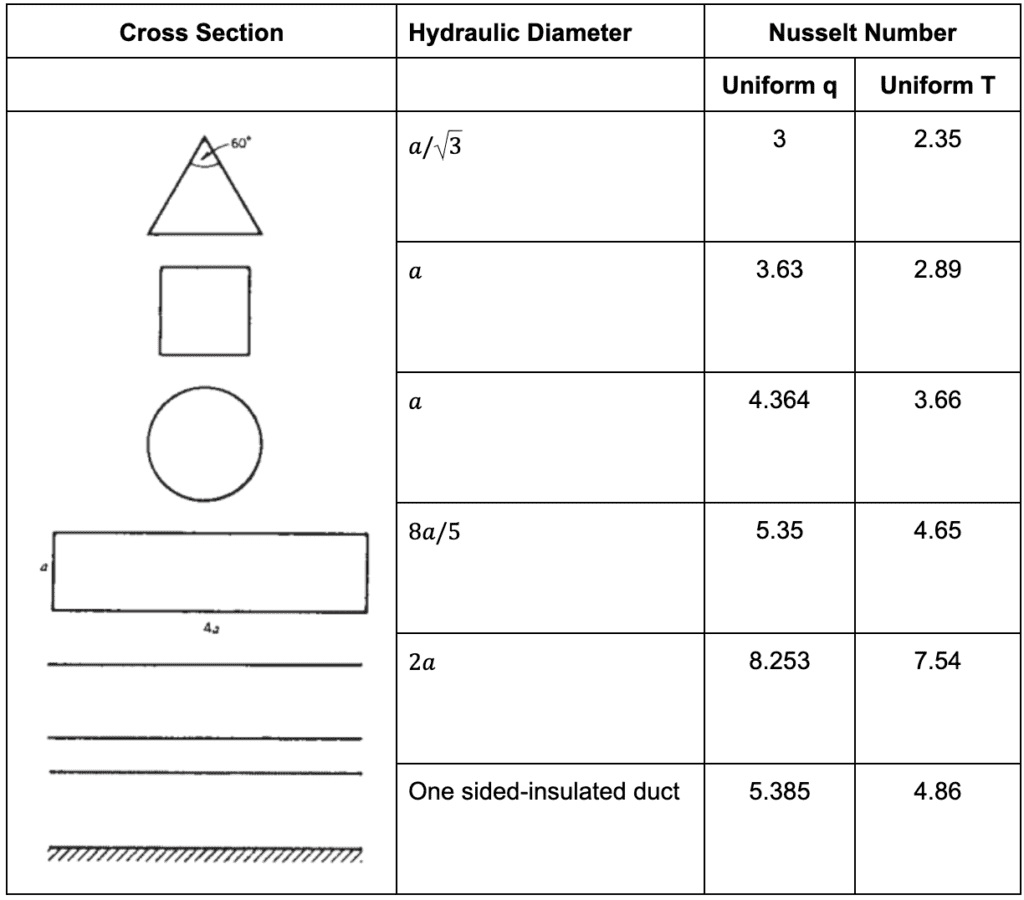
くさびを通過する流れに対する対流熱伝達
縦方向の圧力差が存在し、壁が等温である場合、くさびを通過する流れの局所ヌセルト数には次の値が適用されます:

下の表は、異なるくさび角とプラントル数に対する\(\frac{Nu}{{{Re}_x}^\frac{1}{2}}\) の値を示しており、これは局所対流熱伝達率の計算に使用することができます。
平均熱伝達率は局所熱伝達率から以下の関係式で導かれます:
$$h_{avg} = \frac{2h}{1+m}$$
\(\boldsymbol{\beta}\) |
m |
Pr 0.7 |
Pr 0.8 |
Pr 1 |
Pr 5 |
Pr 10 |
| -0.512 | -0.0753 | 0.242 | 0.253 | 0.272 | 0.457 | 0.570 |
| 0 | 0 | 0.292 | 0.307 | 0.332 | 0.585 | 0.730 |
| \(\frac{\pi}{5}\) | \(\frac{1}{9}\) | 0.331 | 0.348 | 0.378 | 0.669 | 0.851 |
| \(\frac{\pi}{2}\) | \(\frac{1}{3}\) | 0.384 | 0.403 | 0.440 | 0.792 | 1.013 |
| \(\pi\) | 1 | 0.496 | 0.523 | 0.570 | 1.043 | 1.344 |
| \(\frac{8\pi}{5}\) | 4 | 0.813 | 0.858 | 0.938 | 1.736 | 2.236 |
自然対流
対流熱伝達率のスケール解析
以下は、長さ\( H\) の 2 次元曲面が鉛直方向に配置され、重力\(g\)がその表面の法線方向に対して垂直( \(-y\) 方向)に作用させた場合のスケール解析です。強制対流で用いるのと同様の論理を使って、境界内における運動量と熱エネルギーの方程式を導出することができます。強制対流の場合とは異なり、ここでは境界層がy軸方向に沿って発達していくため、熱境界層の厚さ\(\delta_T << H\)となり、その結果として\(\frac{\partial^2 T}{{\partial y}^2}\)の項は \(\frac{\partial^2 T}{{\partial x}^2}\)に比べて非常に小さくなります。
強制対流の場合とは異なり、境界層は y 軸方向に発達していることに注意してください。
$$u \frac{\partial T}{\partial x} + v \frac{\partial T}{\partial y} = \alpha \left(\frac{\partial^2 T}{\partial x^2}\right)$$
$$\rho \left(u \frac{\partial v}{\partial x} + v \frac{\partial v}{\partial y}\right) = – \frac{{\Delta P}_\infty}{\Delta y} + \mu \left(\frac{\partial^2 v}{\partial x^2}\right) – \rho g$$
$$\rho \left(u \frac{\partial v}{\partial x} + v \frac{\partial v}{\partial y}\right) = \mu \left(\frac{\partial^2 v}{\partial x^2}\right) + \left(\rho_\infty – \rho\right)g$$
この式は体積膨張係数\(\beta\) で書き直すと次のようになります:
$$\rho \left(u \frac{\partial v}{\partial x} + v \frac{\partial v}{\partial y}\right) = \mu \left(\frac{\partial^2 v}{\partial x^2}\right) + \beta \left(T – T_\infty\right)g$$
エネルギー方程式は次のようになります:
$$\frac{u\Delta T}{\delta_T} , \frac{v\Delta T}{H} \sim \alpha \frac{\Delta T}{{\delta_T}^2}$$
連続の式から、次の関係が成り立ちます:
$$\frac{u}{\delta_T} \sim \frac{v}{H}$$
上記の2つの方程式を使用すると、次の関係が得られます:
$$v \sim \alpha \frac{H}{{\delta_T}^2}$$
運動量の方程式の項の大きさの順序は以下の通りです:
$$\frac{vu}{\delta_T} , \frac{v^2}{H} , \nu \frac{v}{{\delta_T}^2} , g\beta \Delta T$$
プラントル数やレイリー数などの無次元量を用いると、以下の式が得られます:
$$\left(\frac{H}{\delta_T}\right)^4 {{Ra}_H}^{-1 }{{Pr}^{-1}} , \left(\frac{H}{\delta_T}\right)^4 {{Ra}_H}^{-1} , 1 $$
ここで、レイリー数は次のように定義されます:
$${Ra}_H = \frac{{g \beta \Delta TH}^3}{\alpha \nu}$$
\(Pr >> 1\) では、浮力と摩擦のバランスがとれています:
$$\text{Nu} = \frac{hH}{k} \sim {{Ra}_H}^\frac{1}{4}$$
\(Pr << 1\) の場合、浮力と慣性が釣り合い、\(Nu\)の間に次の関係が得られます:
$$\text{Nu} = \frac{hH}{k} \sim \left({Ra}_H \cdot Pr\right)^\frac{1}{4}$$
対流熱伝達係数/ヌセルト数のさまざまな式とは?
垂直プレート上の層流の対流熱伝達率
垂直等温平板を通過する自然対流の積分解は次のようになります。
$$\text{Nu} = 0.783 {{Ra}_y}^\frac{1}{4} \text{ and Nu } = 0.689 \left({Ra}_y \cdot Pr\right)^\frac{1}{4}$$
それぞれ\(Pr >> 1\) と\(Pr << 1\) について、類似解を用いると、次のようになります:
$$\text{Nu} = 0.503 {{Ra}_y}^\frac{1}{4} \text{ and Nu } = 0.6 \left({Ra}_y \cdot Pr\right)^\frac{1}{4}$$
平均\(Nu\)の値は次のようになります:
$$\text{Nu} = 0.671 {{Ra}_H}^\frac{1}{4} \text{ and Nu } = 0.8 \left({Ra}_H \cdot Pr\right)^\frac{1}{4}$$
熱流束が一定の場合、ヌセルト数の値は次のようになります:
$$\text{Nu} = \frac{2}{{360}^\frac{1}{5}} \left(\frac{Pr}{\frac{4}{5} + Pr}\right)^\frac{1}{5} {{Ra}_{*y}}^\frac{1}{5}$$
ここで、レイリー数は次のように定義されます:
$${Ra}_H = \frac{{g \beta H}^4 q”}{\alpha \nu k}$$
ここで、各物理量は以下の通りです。
\(q" = \): 熱流束
\(k = \): 熱伝導率
\(y = \): 熱境界層開始点からの垂直プレートの長さ
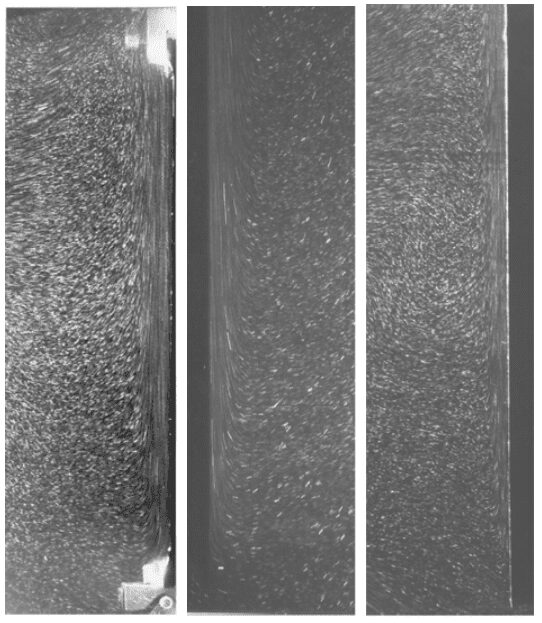
垂直面上の乱流2次元流れに対する対流熱伝達率
乱流の場合、平均ヌセルト数の式は以下のようになります:
$${Nu}_H = \left(0.825 + \frac{0.387{{Ra}_H}^\frac{1}{6}}{\left(1 + \left(\frac{0.492}{Pr}\right)^\frac{9}{16}\right)^\frac{8}{27}}\right)^2$$
ここで、レイリー数およびプラントル数は、壁と流れの温度の平均に対して計算されます。熱流束が一定で乱流条件の場合、ヌセルト数は次のように計算されます:
$$\text{Nu } = 0.645 {{Ra}_{*H}}^{0.22}$$
傾斜壁の対流熱伝達率
傾斜壁の場合、ヌセルト数の式は変わらず、傾斜の影響は次のようにレイリー数で説明されます:
$${Ra}_H = \frac{cos\left(\phi \right)g \beta H^4 q”}{\alpha \nu k} \text{ and } {Ra}_H = \frac{cos\left(\phi \right)g \beta \Delta T H^3}{\alpha \nu}$$
ここで、\(\phi\) は重力方向に対する壁面の角度です。

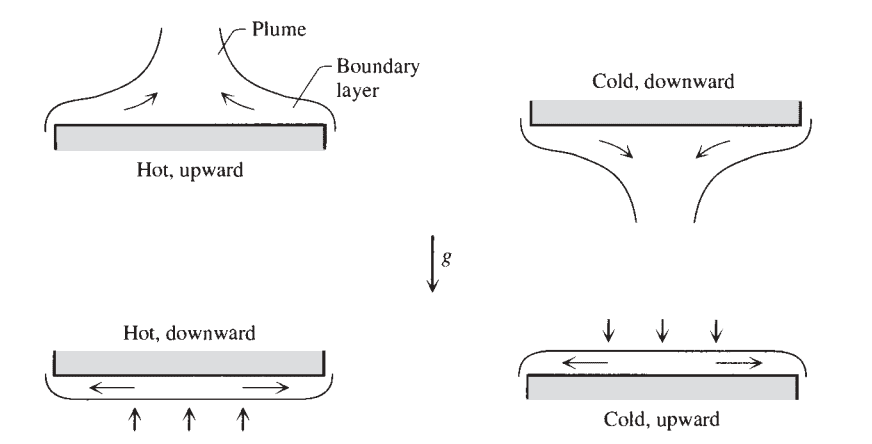
水平面の対流熱伝達率
上向きの高温面または下向きの低温面のヌセルト数の値は以下の通りです:
$$Nu = 0.54 {{Ra}_H}^\frac{1}{4} \text{ for } \left({10}^4 < {Ra}_H < {10}^7\right)$$
$$Nu = 0.15 {{Ra}_H}^\frac{1}{3} \text{ for } \left({10}^7 < {Ra}_H < {10}^9\right)$$
熱面が下向き、冷面が上向きの場合、ヌセルト数の式は次のようになります:
$$Nu = 0.27 {{Ra}_H}^\frac{1}{4} \text{ for } \left({10}^5 < {Ra}_H < {10}^{10}\right)$$
水平円筒の対流熱伝達率
回転軸が重力方向に垂直な水平等温円柱の場合、ヌセルト数は以下のようになります:
$${Nu}_D = \left(0.6 + \frac{0.387{{Ra}_D}^\frac{1}{6}}{\left(1 + \left(\frac{0.599}{Pr}\right)^\frac{9}{16}\right)^\frac{8}{27}}\right)^2$$
ここで、\({Nu}_D = \frac{hD}{k} \)、\({Ra}_D = \frac{g \beta \Delta T D^3}{\alpha \nu}\)です。
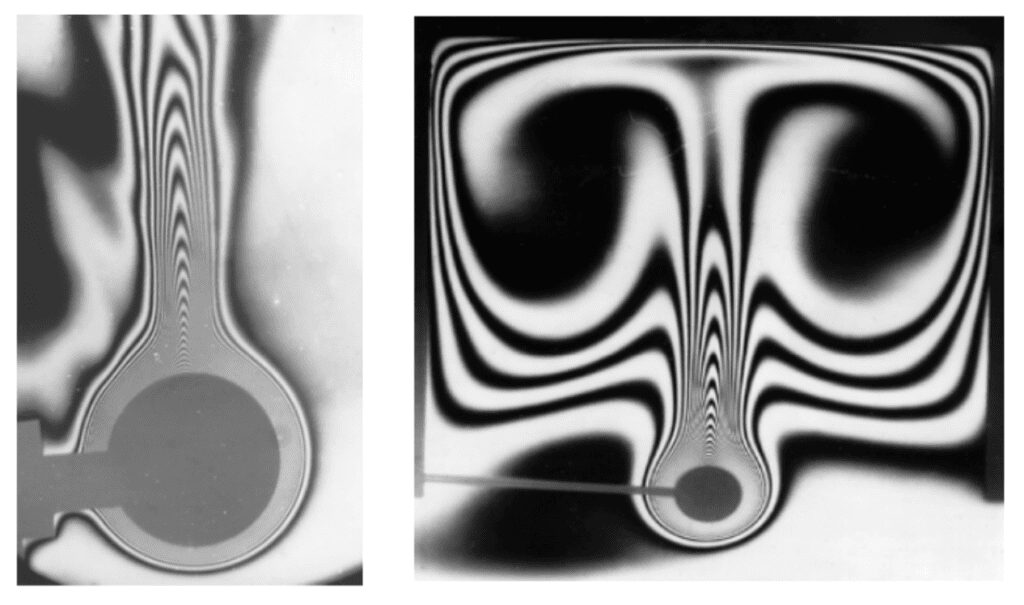
垂直円筒の対流熱伝達率
等温垂直円筒の場合、ヌセルト数の式は以下のようになります:
$${Nu}_H = \frac{4}{3} \left(\frac{7{Ra}_{H}Pr}{5\left(20 + 21Pr\right)}\right)^\frac{1}{4} + \frac{4\left(272 + 315Pr\right)H}{35\left(64 + 63Pr\right)D}$$
球の対流熱伝達率
等温球の場合、式は次のようになります:
$${Nu}_D = \left(2 + \frac{0.589 {{Ra}_D}^\frac{1}{4}}{\left(1 + \left(\frac{0.469}{Pr}\right)^\frac{9}{16}\right)^\frac{4}{9}}\right)$$
\(Pr > 0.7 \text{ and } {Ra}_D < 10^{11}\)
任意形状の物体の対流熱伝達率
任意の形状の等温体について、長さは次のように定義されます:
$$\gamma = A^\frac{1}{2}$$
ここで、\(A\)は流体と接触している物体の表面積です。
上記の長さスケールは、ヌセルト数とレイリー数の両方に使用されます:
$${Nu}_\gamma = \left({{Nu}_\gamma}^0 + \frac{{0.67G_\gamma {Ra}_\gamma}^\frac{1}{4}}{\left(1 + \left(\frac{0.492}{Pr}\right)^\frac{9}{16}\right)^\frac{4}{9}}\right)$$
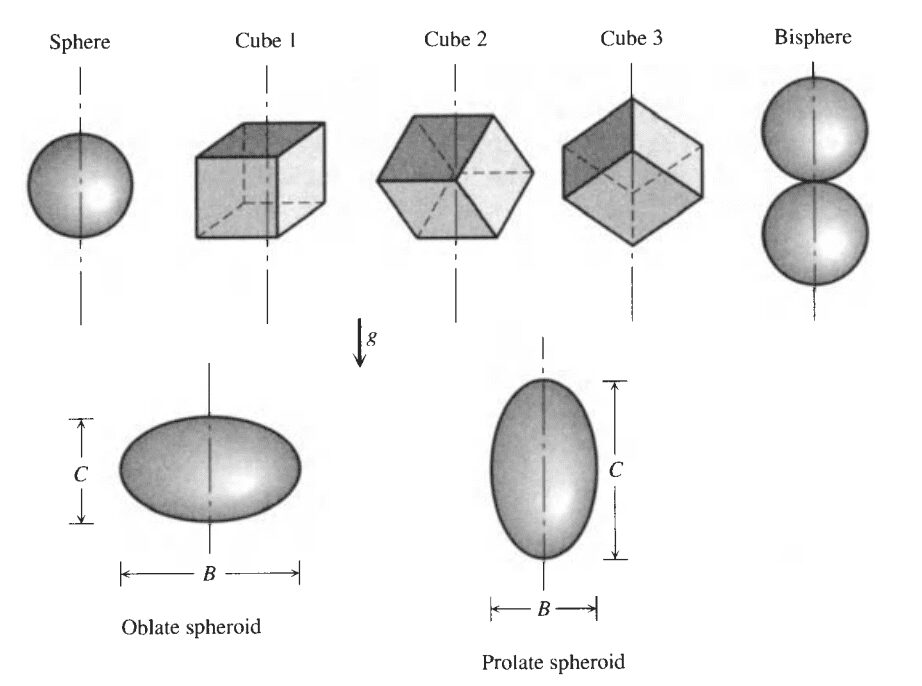
ここで、\({{Nu}_\gamma}^0 \) と\(G_\gamma\) の値は以下の表から求めることができます:
ボディ形状 |
\(\boldsymbol{{Nu}_\gamma}^0\) |
\(\boldsymbol G_\gamma\) |
| 球体 | 3.545 | 1.023 |
| 両球体 | 3.475 | 0.928 |
| 立方体1 | 3.338 | 0.951 |
| キューブ 2 | 3.338 | 0.990 |
| キューブ 3 | 3.338 | 1.014 |
| 垂直短円筒(L~D) | 3.444 | 0.967 |
| 水平短円筒 | 3.444 | 1.019 |
| 45°ショートシリンダー | 3.444 | 1.004 |
| プロレート球状体 (\(\frac{C}{B} = 1.93\)) | 3.566 | 1.012 |
| 肥満球状体 (\(\frac{C}{B} = 0.5\)) | 3.529 | 0.973 |
| 肥満球状体 (\(\frac{C}{B} = 0.1\)) | 3.342 | 0.768 |
垂直発熱板スタックの対流熱伝達率
プレート間の間隔が小さい場合、すなわちプレート間の間隔が熱境界層より小さい場合、全熱伝達率は以下のように計算できます:
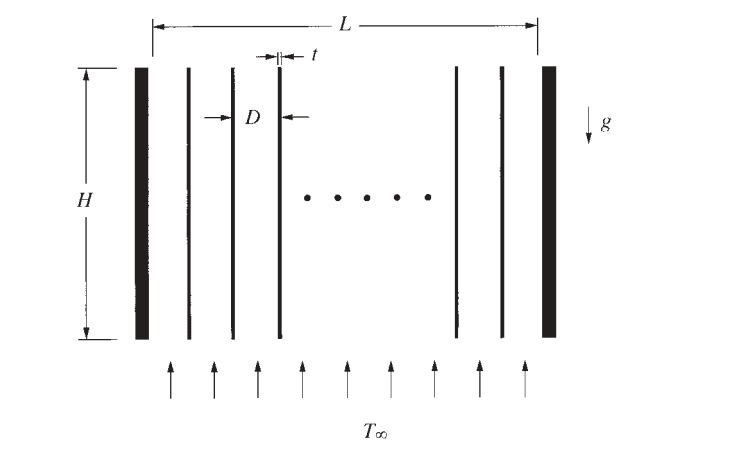
$$q_A = \frac{\rho g \beta C p \left(\Delta T\right)^2 D^3}{12 \nu} W \frac{L}{D}$$
ここで \(W\)は図平面に垂直なプレートの幅です。
プレート間の間隔が、形成される境界層の厚さよりも十分に大きい\(D > {H{Ra}_H}^{-\frac{1}{4}}\) 場合、熱伝達の式は次のようになります:
$$q_A = 2 \frac{k}{H} W H \Delta T \frac{L}{D} 0.516{{Ra}_H}^\frac{1}{4}$$
CFDによる熱流体シミュレーション
数値流体力学(CFD)は様々なスケールや問題に対して対流を研究することができます。例えば、CFD は、LES や DNS シミュレーションを用いた対流で発生する流れのパターンの学術的な理解や、RANS シミュレーションを用いた大規模な工業スケールの問題の理解に使用することができます。

CFDによる対流のシミュレーション
CFD では温度差があり、重力方向が指定されている場合(自然対流)、または流れが定義されている場合(強制対流)に対流が発生します。温度勾配は様々な方法で設定することができます。ここで重要なことは、エネルギー方程式を組み込んだソルバーが必要であるということです。非圧縮性の等温ソルバーは、この種の研究には適していません。
境界条件
境界条件とは、流れ領域の境界面において、ある問題について我々が知っているすべての事柄を定義することです。対流 CFD シミュレーションでは、温度、電力、熱流束、熱伝導率などが該当します。通常、これによって温度勾配が形成され、前のセクションで説明したように、CFDによって流れのパターンが計算されます。
熱源 (Volumetric sources)
通常、電力または体積電力(立方メートルあたり)として定義される熱源は、発熱をモデル化するのに適した方法です。例えば、オフィスの部屋では、人や機器が熱を放出します。しかし、それらは常に静的であるとは限りません。数値解析では、発熱源を体積を持つモデルで表現し、各発熱モデルは空間内を動的に移動させることもできます。
重力とその方向
自然対流は浮力によって駆動されます。すなわち、空気が加熱されると密度が減少し、重力とは反対の方向に移動します。この意味で、モデルを正しく配置し、重力とその強さを定義することが重要です。ほとんどの場合、重力はZ方向に\(-9.81 \frac{m}{s^2}\)です。しかし、モデルがこの軸に対して正しく配向されていることを確認するためには注意が必要です。流れが強い強制対流の場合は、重力を定義する必要はありません。しかし、CFD シミュレーショ ンのある部分では浮力が強く作用し、他の部分では浮力が作用しないようなシナリオも多くあります。そのため、特定のアプリケーションのために重力の影響を評価することで、興味深い洞察が得られるかもしれません。
参考
- Bejan, A. (2013). Convection Heat Transfer. Wiley.
- Cengel, Y. A., & Ghajar, A. J. (2014). Heat and Mass Transfer: Fundamentals and Applications. McGraw-Hill Education.
- Tardu, S., & Favre-Marinet, M. (2013). Convective Heat Transfer: Solved Problems. Wiley.
- Khramtsov, P. P., & Martynenko, O. G. (2010). Free-Convective Heat Transfer: With Many Photographs of Flows and Heat Exchange. Springer.
- A-priori evaluation of data-driven models for large-eddy simulations in natural convection – Scientific Figure on ResearchGate. Available from: https://www.researchgate.net/figure/The-instantaneous-DNS-result-of-Rayleigh-Bernard-convection-in-cubic-cell-for-Ra-50_fig1_346991765 [accessed 28 Dec, 2022]
対流と合わせて読みたい
SimScale製品紹介資料ダウンロード

SimScaleの特徴と計算事例をまとめた資料を用意しております。