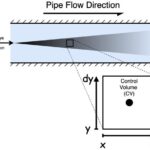
フィックの法則は、濃度の高い場所から低い場所へと粒子が移動する現象を説明するものです。この移動は「拡散」と呼ばれ、圧力差によって生じるバルクフロー (流れ全体の動き) とは無関係に起こります。
流体流の拡散をシミュレーションする際には、これを「スカラー混合」または「パッシブスカラー」と呼びます。パッシブスカラーとは、流体中を輸送されるスカラー (濃度など) が、流れそのものには影響を与えないという前提のことです。
この概念を説明するうえでよく使われる例えが、流れの中に染料を注入して流れのパターンを可視化する方法です。染料自体は流れに影響を与えず、流れに従って運ばれるだけであるため、流動の理解に役立ちます。この方法は、研究や教育の現場でも広く活用されています。
より実用的な応用としては、性質の近い2種類の流体がどのように混ざり合うかを調べる際の近似手法としても利用されます。たとえば、空気と一酸化炭素は物性が非常に近いため、SimScaleでは非圧縮性流れ+パッシブスカラーの組み合わせによって、それらの混合挙動を簡易的に再現することができます。
| 物質 | 密度 \(kg/m^3\) | 動粘度 \(Pa\cdot s\) |
|---|---|---|
| 空気 | 1.29 | 1.72 x 10-5 |
| 一酸化炭素 | 1.25 | 1.66 x 10-5 |
拡散の法則の歴史
アドルフ・フィックは、19世紀半ばに拡散に関する研究を始めました。彼の実験は、2つのリザーバーの間に塩溶液を配置し、濃度の違いによってどのように物質が移動するかを測定するというものでした。
当時の彼の対象は主に流体中の拡散でしたが、現在ではこのフィックの法則は、固体・液体・気体を問わず、あらゆる媒質での拡散を説明する基本法則として広く使われています。
なお、拡散の中には、フィックの法則に従わない特殊な拡散現象もあり、それらは「非フィック拡散 (non-Fickian diffusion)」と呼ばれています。
フィックの法則とは?
フィックの法則には、第一法則と第二法則の2つがあり、拡散現象を空間的な広がりと時間的な変化の両面から説明します。
フィックの第一法則 (定常状態の拡散)
フィックの第一法則は、拡散フラックス (物質の移動量) が濃度勾配に比例することを示します4。
「濃度が高いところから低いところへ、物質は一定の割合で流れていく」という直観的にも理解しやすい法則です。
1次元の場合の典型的な式は以下の通りです2:
$$J = -D\frac{d \varphi}{dx}\tag{1}$$
- \(J\): 拡散フラックス (単位面積当たりの移動量/時間)
- \(D\): 拡散係数 (移動のしやすさを示す定数)
- \(\varphi\): 濃度 (例: \(mol/m^3\))
- \(x\): 位置
マイナス符号は、「高濃度から低濃度へ移動する」ことを意味します。
フィックの第二法則 (非定常の拡散)
第二法則は、時間の経過に伴う濃度分布の変化を記述するもの4で、偏微分方程式の形になります:
$$\frac{\delta \varphi}{\delta t} = D\frac{\delta^2 \varphi}{\delta x^2}\tag{2}$$
- \(\varphi\): 濃度 (例: \(mol/m^3\))
- \(t\): 時間
- \(x\): 位置
- \(D\): 拡散係数
この式は、拡散によって濃度がどのように滑らかになっていくかを定量的に示しており、時間的な濃度変化のシミュレーションに広く使われます。
拡散係数とは?
拡散係数とは、2つの物質 (種) がどれくらいの速さで互いに拡散するかを示す定数です。この値が大きいほど、物質はより速く広がっていきます。
単位は\(\frac{長さ^2}{時間}\)で表され、一般的には\(m^2/s\)や\(cm^2/s\)が使われます。
拡散係数の例と取得方法
特定の物質の組み合わせ (種のペア) に対する拡散係数は、主に実験データに基づいて決定されます。
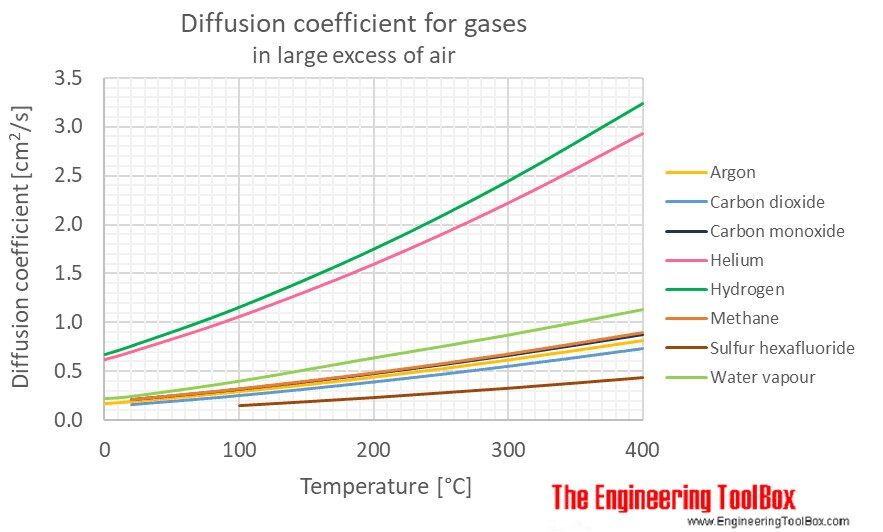
よく知られている例としては、以下のような空気中での拡散係数があります:
- アルゴン
- メタン
- 二酸化炭素
- 一酸化炭素 など
これらのデータは、Engineering Toolboxなどの技術リファレンスサイトでも公開されています。
SimScaleでの拡散シミュレーション
SimScaleでは、拡散現象をパッシブスカラーとして扱う機能が用意されています。この機能は現在、以下の解析タイプでサポートされています:
- 非圧縮性流れ (Incompressible)
- 対流熱伝達 (Convective Heat Trasnfer)
- 共役熱伝達 v2.0 (Conjugate Heat Transfer v2.0)
- 共役熱伝達 埋め込み境界法 (Conjugate Heat Transfer IBM)
最大で10 種類までのパッシブスカラーを同時に取り扱うことができます。
各スカラーごとに拡散係数 (Diffusion Coefficient) を設定できます。これはシミュレーションツリー内のModel -> Passive scalarにて定義され、デフォルト値は\(1\times10^{-5}m^2/s\)です。
例1: 煙突の煙の伝搬 (SimScaleチューリアルより)
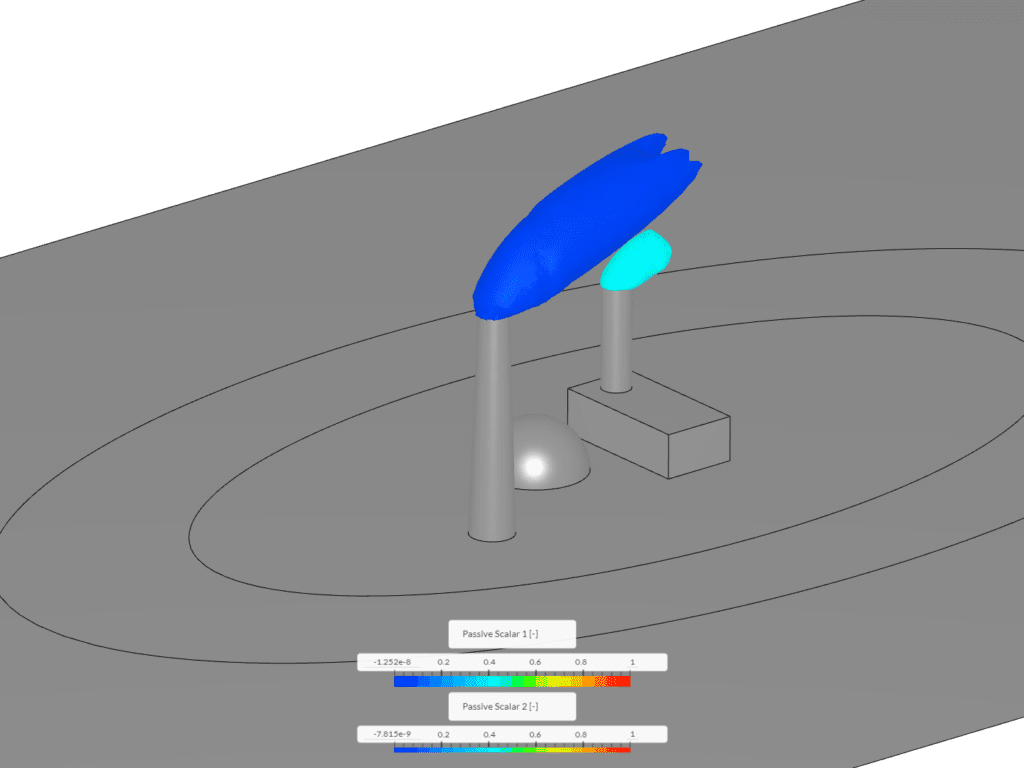
以下の図は、SimScaleの公式チュートリアル「煙突からの煙の伝搬」で得られた結果の一部です。このケースでは、2種類のスカラー (スカラー1, スカラー2)を使用しており:
- スカラー1: 煙突からの排気
- スカラー2: 建物からの排気
を表しています。どちらも空気と混合されながら拡散していきます。下図は、スカラー濃度が0.1~1の範囲にある領域を等値ボリューム (Iso Volume) として可視化したものです。
例2: 駐車場の汚染 (SimScaleチュートリアルより)
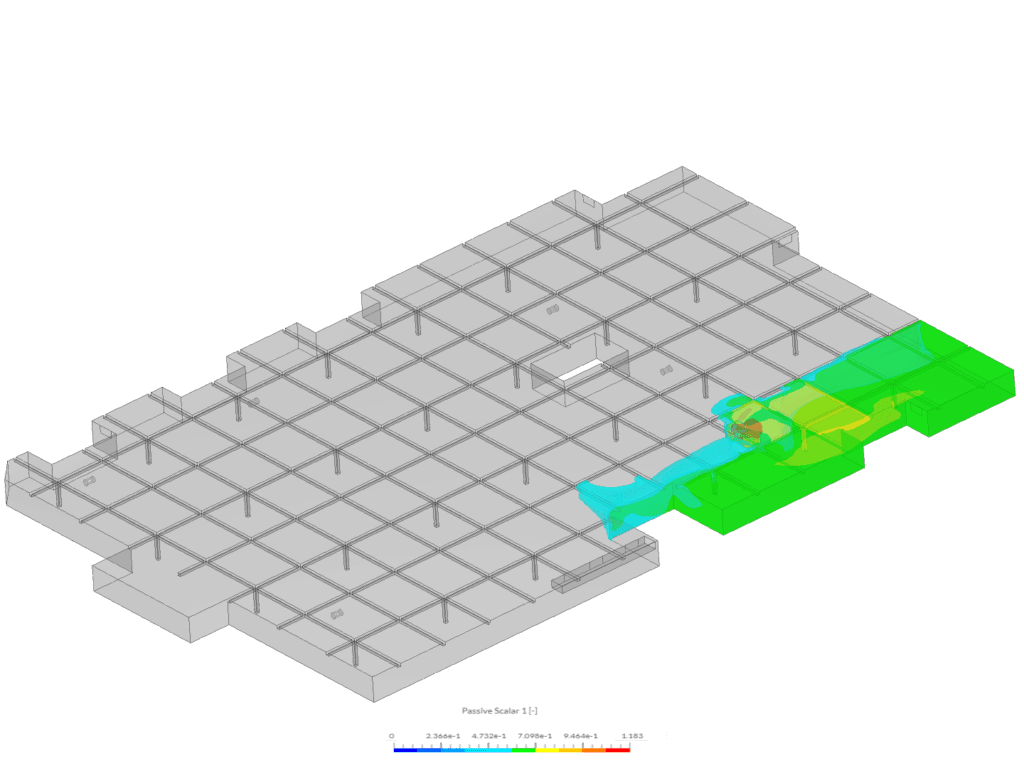
以下の図は、SimScaleの公式チュートリアル「駐車場の排気ガスシミュレーション」で得られた結果の一部です。スカラー濃度が0.5~1.183の範囲ある領域を等値ボリューム (Iso Volume) として可視化したものです。
このシミュレーションでは、スカラー1が地下駐車場内の自動車から排出された一酸化炭素 (CO) を表し、換気状況に応じた濃度分布の変化を確認することができます。
SimScaleを使えば、こうした屋内空間での有害物質の拡散状況を視覚的に把握できるため、換気計画や安全対策の検討に非常に役に立ちます。
SimScaleで今すぐ試してみる!
SimScaleでは、このようにパッシブスカラーを使った拡散解析を通じて、実際の建築設備設計や環境安全対策にも応用できる洞察が得られます。
ここでご紹介したチュートリアルをはじめ、SimScaleでは今すぐシミュレーションを無料で始められます。登録はわずか1分。クレジットカードの登録も不要です。
SimScale製品紹介資料ダウンロード

SimScaleの特徴と計算事例をまとめた資料を用意しております。