疲労解析は、高い耐久性と信頼性が求められる製品を設計し、最適化する上で非常に重要なステップです。疲労解析は、故障のポイントを特定し、製品の誤動作、リコール、あるいは大惨事を防ぐのに役立ちます。予想される部品の負荷をシミュレートすることにより、エンジニアは耐疲労性、信頼性、および性能のために設計を最適化することができます。

疲労とは？

疲労は、材料が繰り返し荷重を受けたときに発生する材料の破壊メカニズムです。疲労破壊では、印加される応力が降伏応力または1回の荷重印加で材料を損傷するのに必要な応力よりも低いにもかかわらず、繰り返し荷重を受けると材料に亀裂が形成されます。

疲労の種類

疲労には主に2つのタイプがあります:

• 低サイクル疲労
  応力振幅が材料の降伏応力よりわずかに小さく、サイクル数がかなり少ない(10,000サイクル未満)ために材料に亀裂が生じ、破損する場合。
• 高サイクル疲労
  応力振幅が材料の降伏応力よりはるかに小さく、サイクル数がかなり多い(10,000サイクル以上)ために材料に亀裂が生じ、破損する場合。

図1: 疲労破壊した旅客機ガスタービンエンジンの航空宇宙用金属ディスク¹

疲労破壊の3つの段階

疲労破壊は、負荷の繰返し性によって起こる進行性のプロセスです。このため、材料に微細な欠陥が生じ、その欠陥は次第に巨視的な亀裂へと成長します。それ以降、疲労は3つの段階を経て破壊に至ります:

1. き裂の発生(き裂の形成):
   構造上の不連続面、高温、あるいは溶接欠陥などが原因で、動的荷重が材料表面の応力集中点にかかるとき裂が発生します。き裂の発生領域は極めて小さく、起点の周囲で発生します。き裂が形成されると、応力集中が著しく増大し、繰り返し荷重を受けると、き裂は材料の奥深くまで伝播します。
2. き裂の伝播:
   き裂は成長し始め、材料内を伝播します。クラックの伝播は、クラックノッチ部の応力を決定するために使用される応力拡大係数(K)の測定に基づいて3つのサブステージに分けることができます:
   • Kが小さい場合:
     き裂の進展は材料の微細構造に依存するため、予測は困難。この場合、き裂は全く成長しない可能性があります。
   • Kが増加する場合:
     き裂の伝播速度は、微細構造よりもむしろ材料に依存するようになります。き裂伝播の大部分がこの時期に起こります。
   • Kが大きい場合:
     伝播速度が急速に加速し、材料が保持できなくなり、破壊が起こります。
3. 急速破壊:
   この段階では、材料は繰返し荷重で完全に破壊され、急激に破断します。

疲労解析の方法

疲労解析にはいくつかの方法がありますが、最も顕著なものは次のとおりです:

• 応力-寿命(Stress-Life)法
• ひずみ-寿命(Strain-Life)法
• 線形弾性破壊力学(Linear Elastic Fracture Mechanics | LEFM)法

応力-寿命法

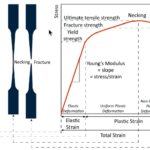
応力-寿命法では、印加応力レベルを破壊までのサイクル数に対してプロットします。応力-寿命法は、予想される応力が材料の弾性限界(降伏点)を超えない場合に高サイクル疲労に使用されます。

したがって、応力-寿命法は、線形材料モデルのFEMシミュレーションでサポートし、予想応力を予測することができます。

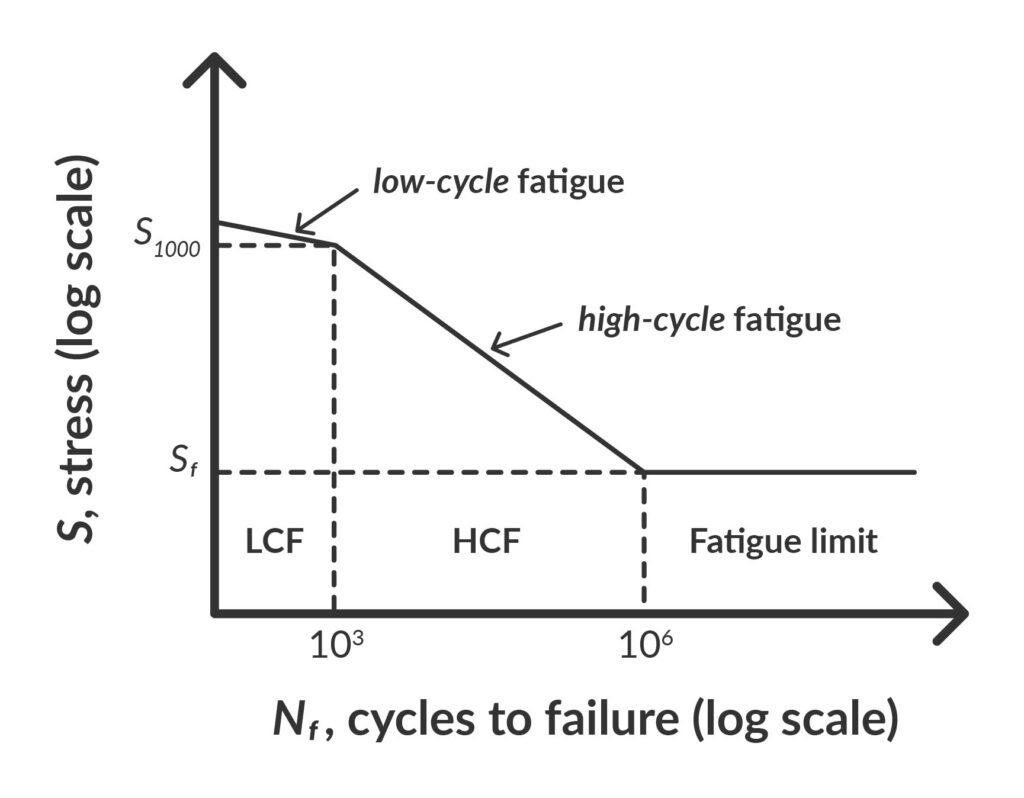
図2: 低サイクル領域と高サイクル領域を示すS-N曲線([2]より引用)

ひずみ寿命法

ひずみ寿命法は、ひずみ振幅を破壊までのサイクル数に対してプロットする方法です。これは、応力の一部が材料の弾性限界(降伏点)を超える場合の低サイクル疲労に使用されます。

したがって、ひずみ寿命法では、予想される応力を予測するために非線形弾塑性材料モデルのFEMシミュレーションが必要になります。

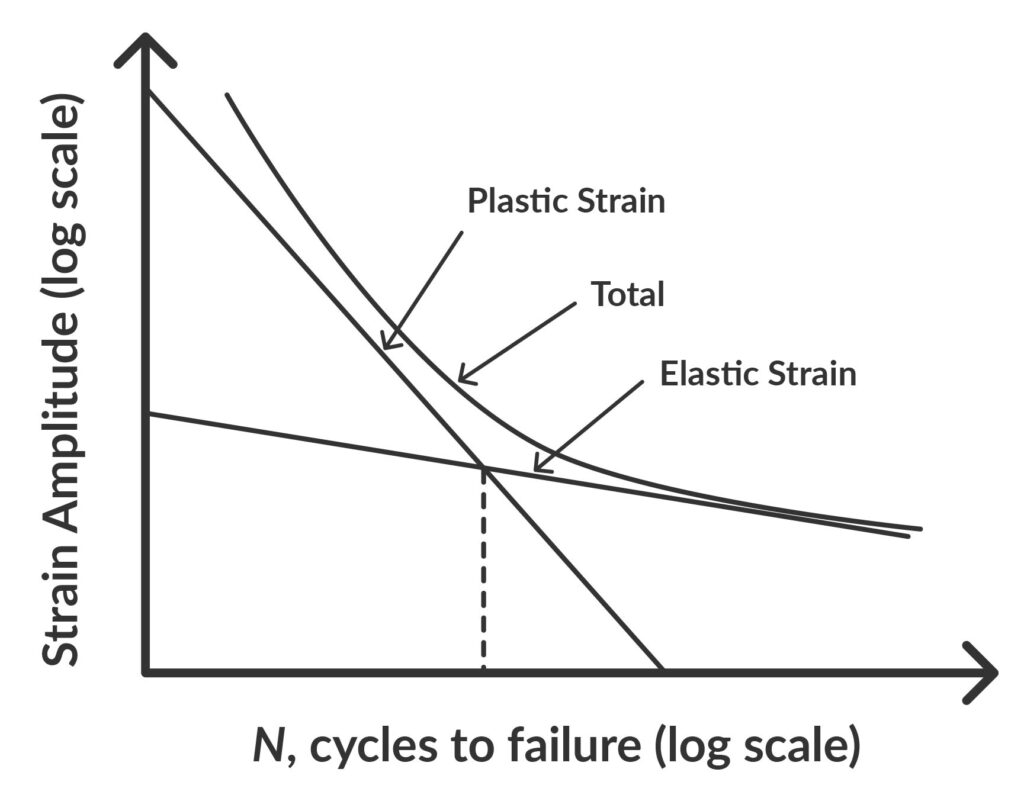
図3: 破壊に至るサイクル数の関数としてのひずみ振幅を示すひずみ寿命曲線([2]より引用)

線形弾性破壊力学(LEFM)法

LEFM法は、疲労き裂の伝播長さを予測するために使用されます。この方法は、き裂の切り欠き部における応力場が弾性である脆性材料の破壊応力を正確に計算します。しかし、延性材料で切欠き部に発生する塑性流動は考慮されていません。塑性域破壊を考慮するには、さらに改良が必要です。これはアーウィンの破壊理論と呼ばれ、グリフィス規準から転用されたもので、弾塑性破壊力学の基礎と言われています。

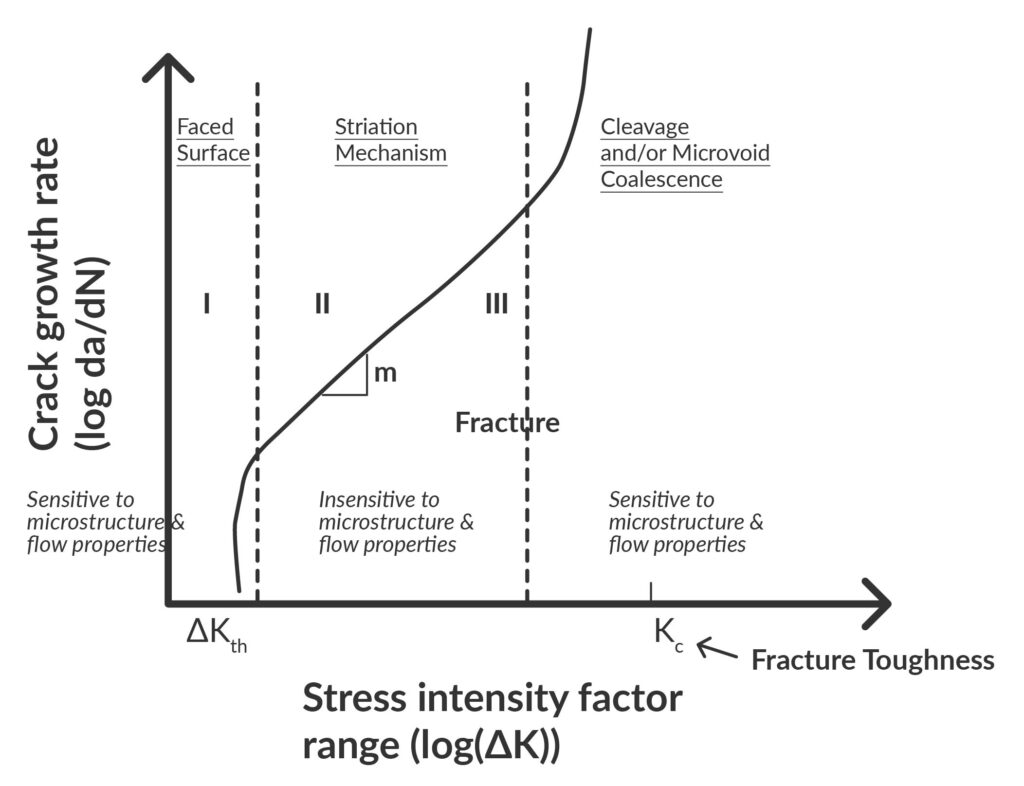
図4: 疲労のマイクロメカニズム([3]より引用)

疲労解析における平均応力補正

平均応力補正は、疲労解析に影響を与えるもう1つの要素です。平均応力補正は、材料疲労に対する変動荷重条件の影響を説明するものです。平均応力補正係数は、駆動力または応力振幅と破壊までのサイクル数を関連付けるS-N曲線を調整するために使用されます。

平均応力補正係数の精度は設計の疲労寿命予測に大きく影響するため、信頼性が高く正確なシミュレーションおよび疲労解析ソフトウェアを使用することが重要です。多くの場合、設計に使用されるS-N曲線は疲労寿命のワーストケースシナリオを想定しているため、平均応力補正係数を使用する必要はありません。

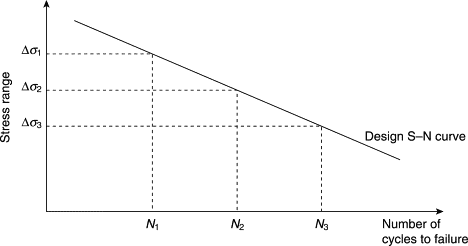
図5: 応力範囲と破断までのサイクル数を相関させた典型的なS-N曲線の例⁴

疲労試験

疲労試験は疲労解析の重要な部分です。疲労試験には、材料または構造に繰返し荷重を与え、その結果生じる疲労損傷を測定することが含まれます。材料と構造の疲労特性と挙動を理解することは、余寿命評価と破壊力学解析に不可欠です。

これらの方法のいずれかを使用してコンポーネントの疲労寿命を正確に予測するには、まず予想される最小応力、平均応力、最大応力、応力振幅、応力範囲、および相関関係を予測する必要があります。そこで役立つのがシミュレーション、特にFEM構造シミュレーションです。

正しい材料特性でコンポーネントに予想される荷重をシミュレートすることで、疲労解析に必要な応力を想定することができます。疲労解析の入力として、フォンミーゼス等価応力または主応力を取ることができます。

図6: SimScaleでシミュレーションしたスチール製コネクティングロッドの静的構造解析とフォンミーゼス応力場

参考

1. Aerospace Testing International
2. Altair OptiStruct
3. Linear Elastic Fracture Mechanics: Part Two, TotalMateria
4. Philippa Moore, Geoff Booth, in The Welding Engineer’s Guide to Fracture and Fatigue, 2015
5. Determination of mechanical properties, J.W. Martin, in Materials for Engineering (Third Edition), 2006