このテストケースの目的は、パイプを流れる非圧縮、定常、層流における以下のパラメータを比較することです。
- 速度
- 圧力降下
SimScaleのシミュレーション結果を、Hagen-Poiseuille方程式\(^1\) を用いて得られた解析結果と比較しました。メッシュはSimScaleプラットフォームのHex-dominantの自動メッシュアルゴリズムで作成しました。
形状
流れ領域として直線円筒パイプを選択しました(図1参照)。面A、B、Cはそれぞれ入口、壁面、出口を表します。
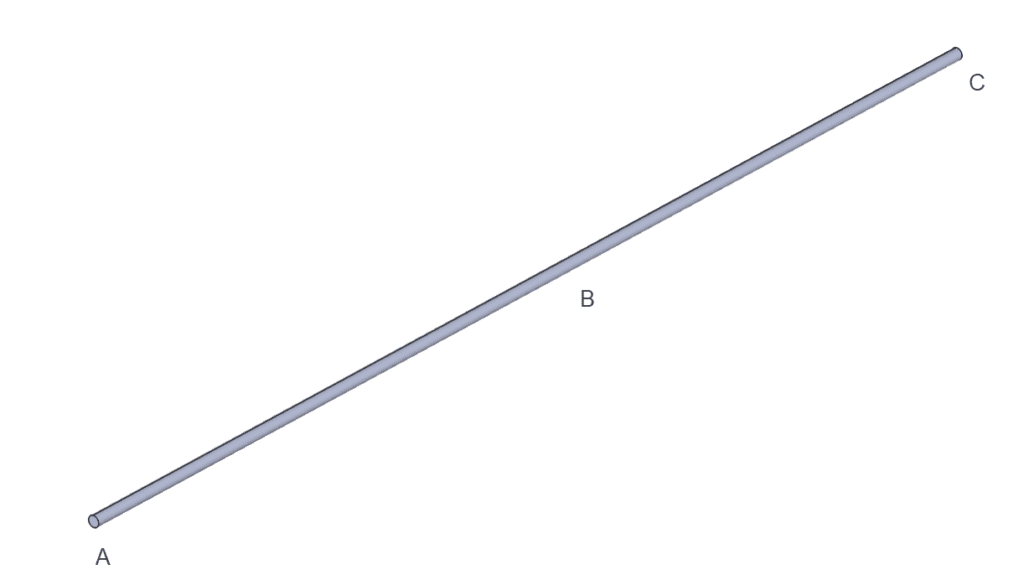
図1: 円筒パイプの形状
| 寸法 | 長さ | 直径 |
| 値\([m]\) | 1 | 0.01 |
解析タイプとメッシュ
ツールの種類
SimScale
解析タイプ
非圧縮定常解析
乱流モデル
層流
メッシュと要素タイプ
SimScaleプラットフォーム上で、Hex-dominant Automaticアルゴリズムを用いて、六面体の構造格子を生成しました(図2参照)。メッシュは成長率1.25で徐々にリファインメントされます。その後、これらのメッシュを使用して結果のメッシュ依存性を検証します。
入口面のセルサイズは他の領域よりも小さくしています。この余分な措置の目的は、入口における放物線状の速度割り当てを捕捉することです。このトピックは次のセクションで詳しく説明します。
グローバルセルサイズとリファインメントサイズは以下のように定義しました。
| メッシュ名 | グローバルセルサイズ\([m]\) | サーフェスリファインメント - 円筒サーフェス\([m]\) | サーフェスリファインメント - インレットサーフェス\([m]\) | セル数 [M] |
| 粗いメッシュ | 0.0016 | 8.00E-04 | 1.00E-04 | 0.435 |
| 中メッシュ | 1.12E-03 | 5.60E-04 | 7.00E-05 | 0.837 |
| ファインメッシュ | 7.84E-04 | 3.92E-04 | 4.90E-05 | 1.700 |
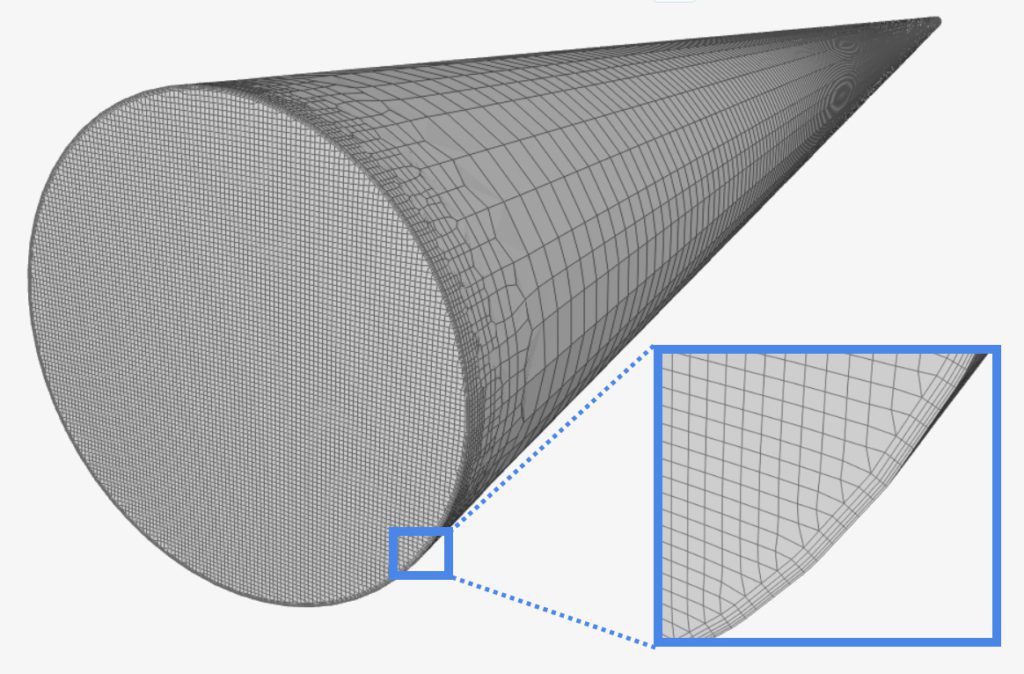
図2: SimScaleのケースで使用した粗いメッシュ
シミュレーションの条件設定
流体
- 水
- 動粘性係数
- \((\nu)\)=10-6 \(\frac{m^2}{s}\)
- 動粘性係数
境界条件
この検証ケースのテーマである注目すべきパラメータの1つは、パイプを通る圧力損失です。特に、ハーゲン・ポアズイユ方程式では、入口での流れが完全に発達していることを考慮します。完全に発達した流れを生成する一般的なCFD手法は2つあります:
- 方法1:
流れが完全に発達するのは、十分な長さを流れた後です。流入面を伸ばすことで、圧力を測定する点での正しい流速分布が得られます。単純な近似として、入口長さをパイプ直径の138倍と考えることができます。レイノルズ数を用いたより複雑な経験式も文献にあります。 - 方法2:
入口で、Hagen-Poiseuille放物線速度方程式と一致する放物線速度分布を定義します。
最初の方法は、メッシュ数が著しく多くなり、計算リソースが必要になるため、現実的ではありません。したがって、このプロジェクトでは放物線速度入力オプションを優先します。
層流の円形パイプを通る放物線速度プロファイルは次のように近似されます:
$$ u_z = u_{z\ max} (1-{r^2 \over R^2}) $$
$$ u_ {z\ max} = 2 \ u_{z\ avg} $$
ここで、\( u_z \) は軸に沿った速度のz成分、\(u_{z\ avg}\) は平均入口速度、\(u_{z\ max}\) は中心線で発生する最大速度、\(r\) は中心線からの半径距離、\(R\) は円形パイプの半径です。\(^2\) 。例えば、円形パイプ内の放物線状の流速分布は図3のようになります。
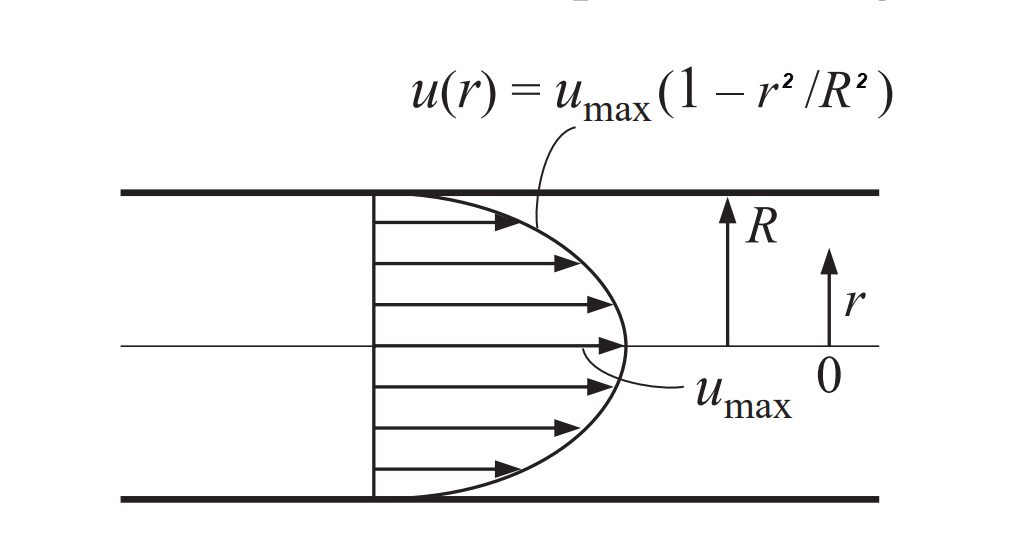
図3: 円管内の完全発達した層流速度分布の模式図(^2)
対応するパイプ表面には以下の境界条件が適用されます:
| 面 | 境界タイプ | 値 |
| 入口 (A) | 速度入口 | 固定値 \(2 \times 0.1 \times (1-(((x)^2+(z)^2)^{0.5/0.005})^2)\) y 方向\(m/s\) |
| 出口 (C) | 圧力出口 | 0 の 固定 値\(Pa\) |
| 壁 (B) | 壁 | 滑りなし |
結果
メッシュごとの圧力損失結果を表4にまとめます:
| メッシュ名 | セル数 [M] | 圧力損失\([Pa]\) |
| 粗いメッシュ | 0.435 | 32.192 |
| 中メッシュ | 0.837 | 32.156 |
| ファインメッシュ | 1.700 | 31.993 |
圧力の結果はメッシュ間で1%未満しか変わりません。粗いメッシュの結果も妥当であると思われますが、細かいメッシュの結果はより正確な結果となっている必要があります。従って、本研究では細かいメッシュの結果を用いて比較を行います。
解析解として、最大軸方向速度、圧力損失、および展開された半径方向速度プロファイルについて以下の式が得られます:
$$u_{z \ max} = 2u_{z \ avg}$$
$$\Delta P = \frac{128}{\pi} \frac{\mu L}{D^4} Q $$
$$u_z = -\frac{1}{4\mu} \frac{\partial p}{\partial z}(R^2 – r^2)$$
ここで
- \( u_{z\ avg} \):平均入口速度\([m/s]\)
- \( u_{z\ max} \):中心線で発生する最大速度\([m/s]\)
- \( u_{z} \):軸に沿った速度\([m/s]\)
- \(r\):中心線からの半径方向距離\([m]\)
- \(R\):円形パイプの半径\([m]\)
- \(\Delta P\):圧力損失\([Pa]\)
- \(\mu\):動粘度\([kg/(m\cdot s)]\)
- \(L\):円管の長さ\([m]\)
- \(D\):円管の直径\([m]\)
- \(Q\):容積流量\([m^3/s]\)
- \(\frac{\partial p}{\partial z}\):パイプに沿った圧力勾配\([Pa/m]\)
です。
SimScaleで得られた流速と圧力損失の解析結果との比較を図4A、4B、4Cに示します。図4Aは、入口と出口における半径方向の流速分布を示しています。
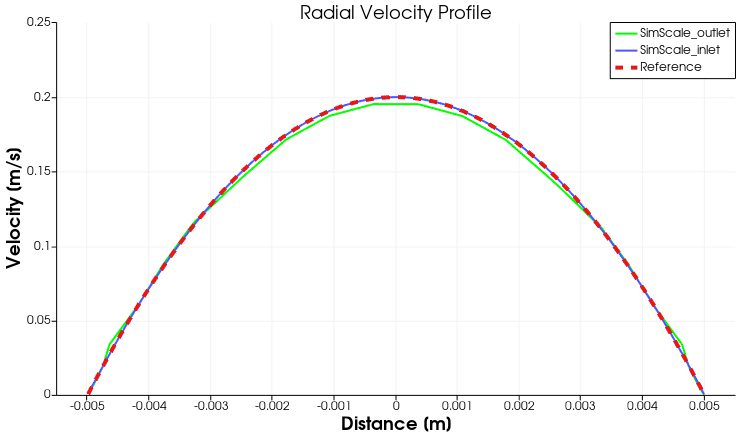
図4A: 入口と出口の半径方向速度分布の比較
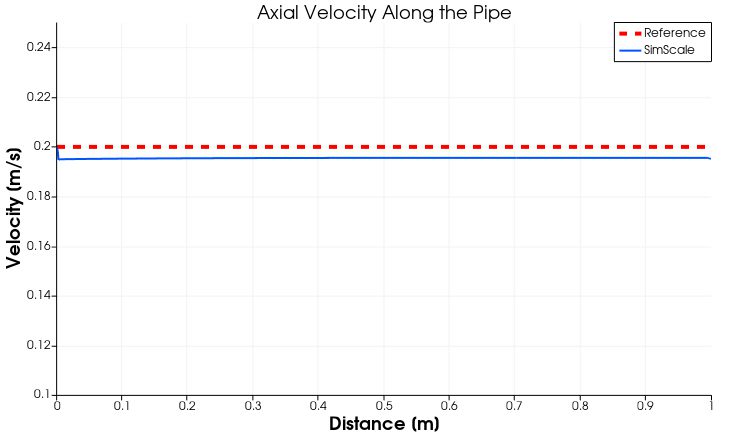
図4B: パイプの中心線に沿った軸方向速度の視覚化
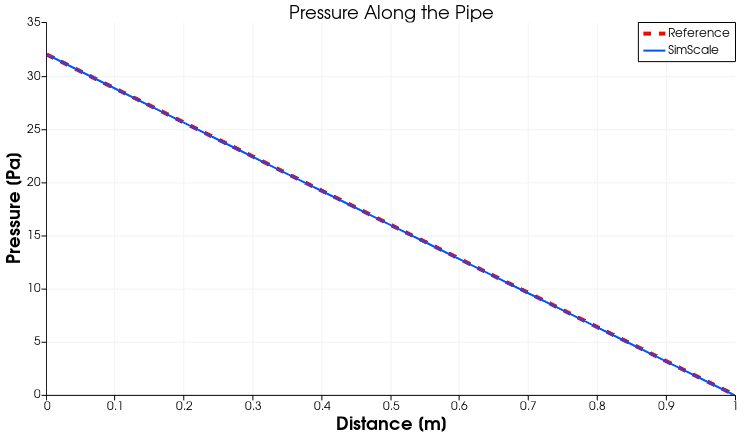
図4C: 配管中心線に沿った圧力
参考
- Hagen–Poiseuille flow from the Navier–Stokes equations
- Çengel, Yunus A. Heat Transfer: A Practical Approach. Boston, Mass: WBC McGraw-Hill, 1998.
SimScaleでは、ウェブブラウザですぐに管内流れから熱や冷却、気体と液体の混相流といった様々な現象の解析をおためしいただけます。
SimScale製品紹介資料ダウンロード

SimScaleの特徴と計算事例をまとめた資料を用意しております。