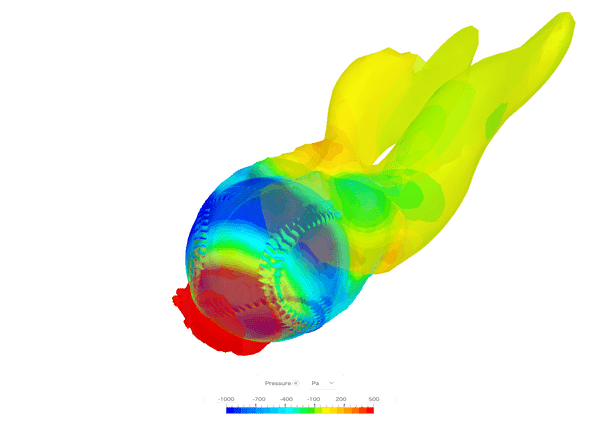
野球のノビのあるストレート : マグヌス効果を味方につける
「ストレートがキャッチャーミットに吸い込まれるように伸びていく。」「バッターの手元でホップした。」
これは単なる比喩ではありません。プロ野球の投手が投げるストレート (フォーシーム) には、実際に「ノビ」を生み出す空気力学が働いています。この記事では、この現象を流体シミュレーション (CFD) を用いて、科学的に紐解いていきます。
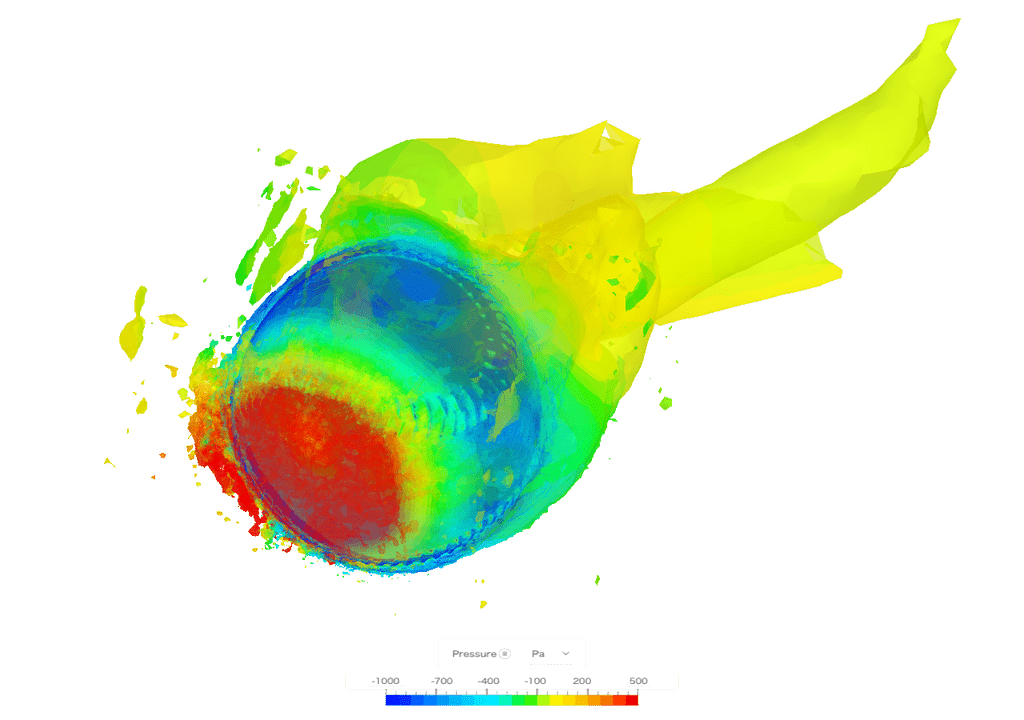
ストレートが投げられた時、ボールの表面には「移動による速度」と「回転による表面速度」の2つの速度が生じます。
ボール上部では両者が同じ向きとなるため、表面の合成速度は大きくなります。反対に下部では両者が逆向きとなり、互いを弱め合うため、合成速度は小さくなります。このようにして、ボールの上下には表面速度の非対称性が生じます。
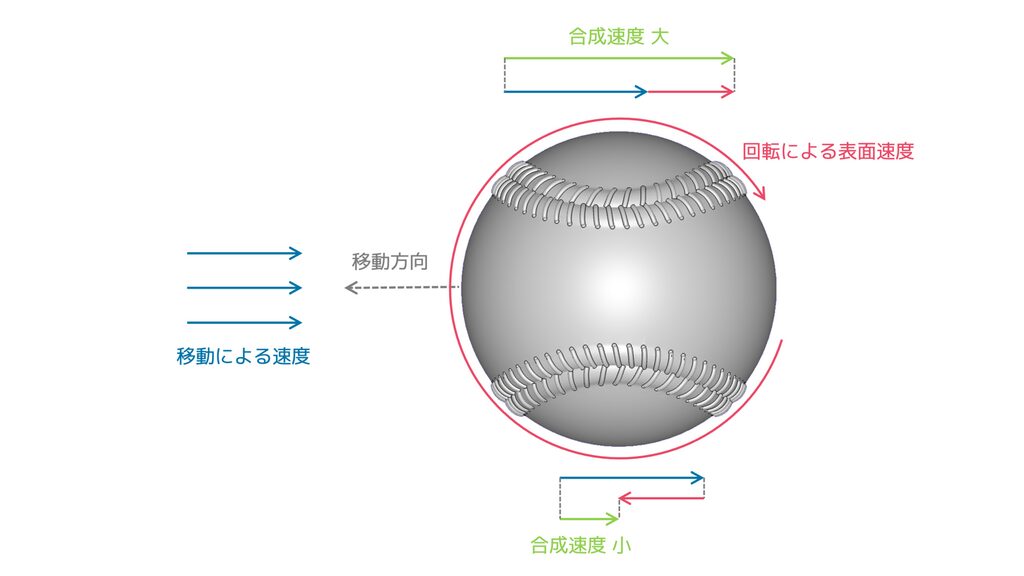
流体力学では、空気の流れが速いほど圧力は小さくなり、遅いほど圧力は大きくなります。これはベルヌーイの法則として知られる関係です。
ストレートの場合、ボールの上下で表面速度に差が生まれるため、同時に圧力差も生じます。
この圧力差が、ボールを上方向に押し上げる力、つまり揚力を発生します。
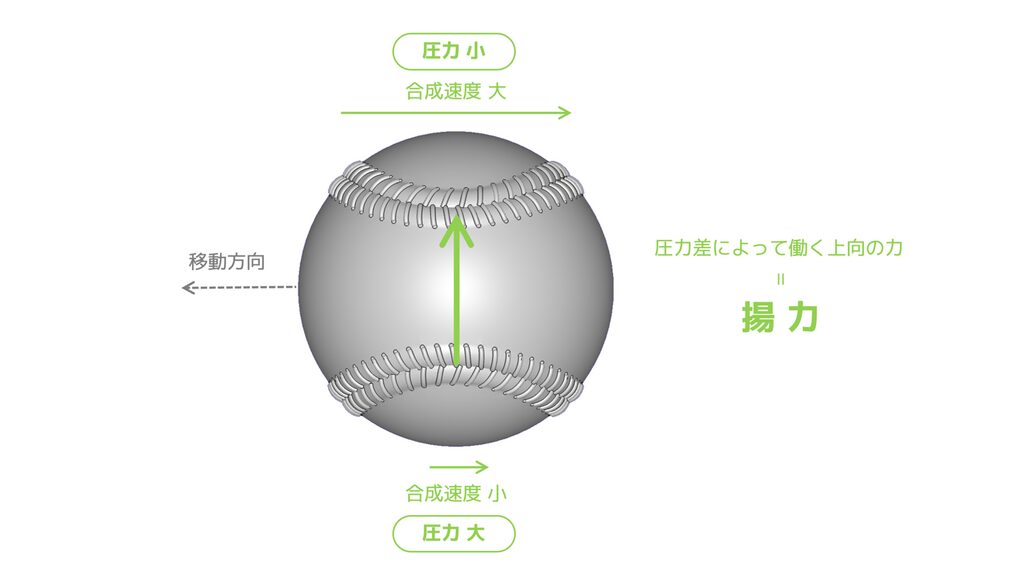
ストレートのように、回転によって生じる揚力を特に「マグヌス効果」と呼びます。
近年、球速だけでなく、回転数や回転軸といった指標が球質を評価する上で重要視されるようになっています。これらの指標は、まさにストレートに働くマグヌス効果の大きさを決める要因そのものです。
では、流体シミュレーションを用いて、このマグヌス効果がどのように生まれているのかを実際に見てみましょう。
1. マグヌス効果を可視化するための投球の流体シミュレーション設定
ストレートの流体シミュレーション (CFD) をSimScaleで実施します。
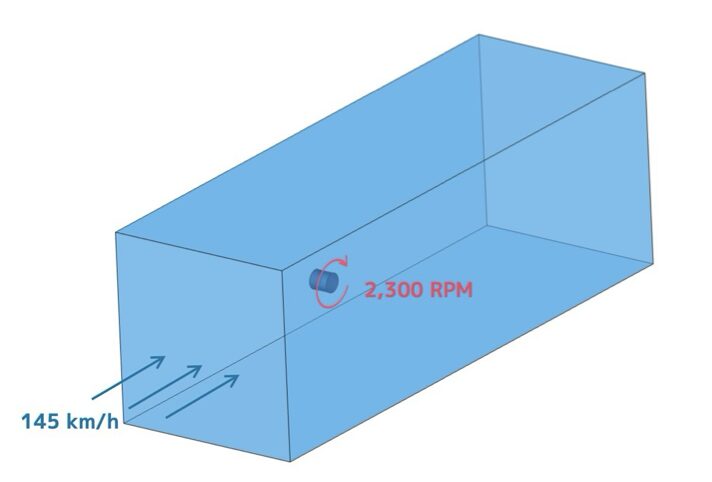
一般的なプロ野球の投手のストレートを検証するために、球速: 145 km/h、回転数: 2,300 RPMとしています。
なお、回転軸は0°で純粋なバックスピンがかかる状態です。
2. ストレートにかかるマグヌス効果の可視化
早速、シミュレーション結果を見てみましょう。
動画では、鉛直断面におけるボール周りの速度分布と、その時刻における揚力の変化を示しています。
揚力は周期的に変動しており、平均値は 1.132 N、ピーク最大値は約 1.45 N となりました。
野球ボールの質量は約 145 g で、重力に換算すると 1.421 Nです。
つまり、マグヌス効果によって重力に匹敵するほどの揚力が発生している ことがわかります。
これは、ストレートの「ノビ」を支える空気力学的な力が、いかに大きいかを示す非常に興味深い結果です。
3. 揚力を決めるもう一つの要素 = シームシフトウェイク (SSW)
ここからは、この揚力の挙動を別の切り口から分析してみます。
なぜ、揚力は周期的に変動するのでしょうか。
その理由を、流れの構造から読み解いていきます。
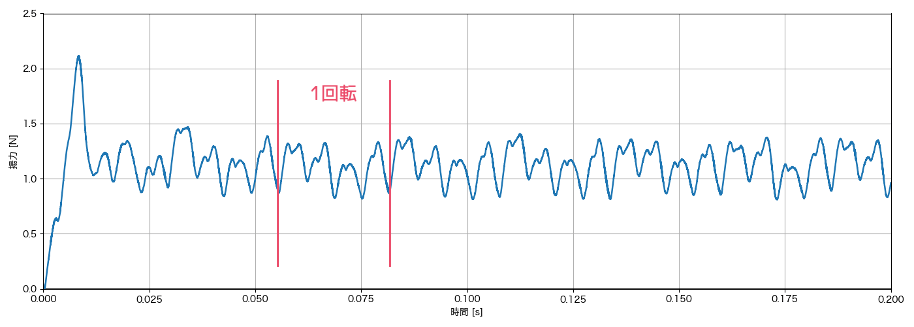
先ほどの揚力のグラフと回転周期を照らし合わせてみると、回転に起因して周期的に変動し、1回転の中で4回ピークが発生していることがわかります。
この周期的な揚力の変動を考察するために、各時間での圧力分布の様子を観察します。
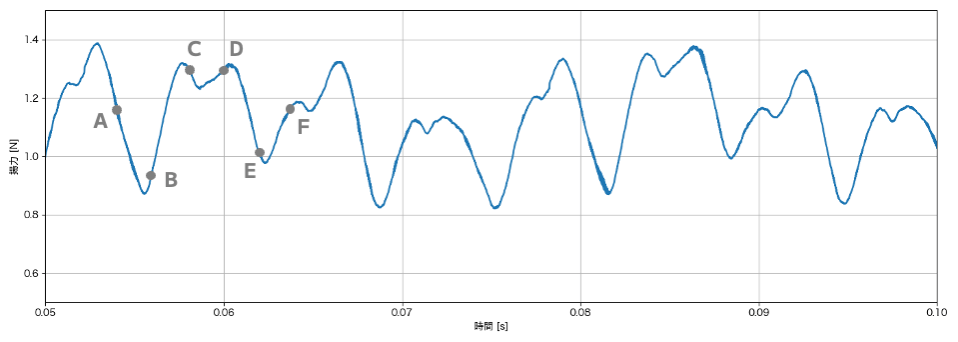
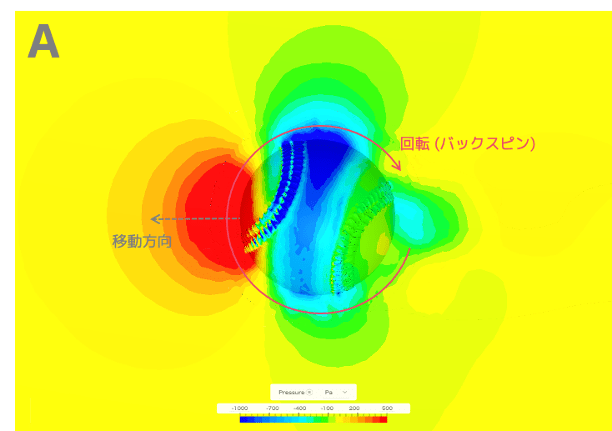
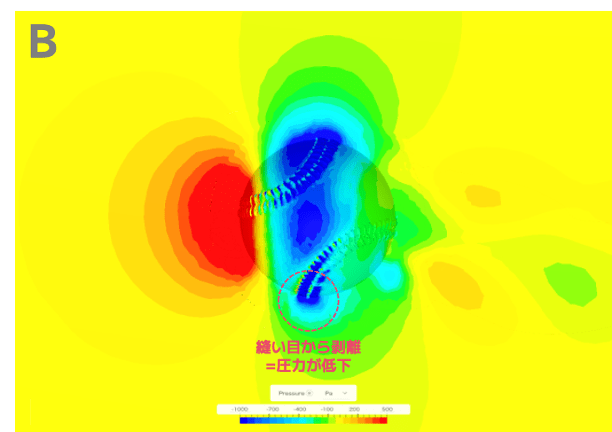
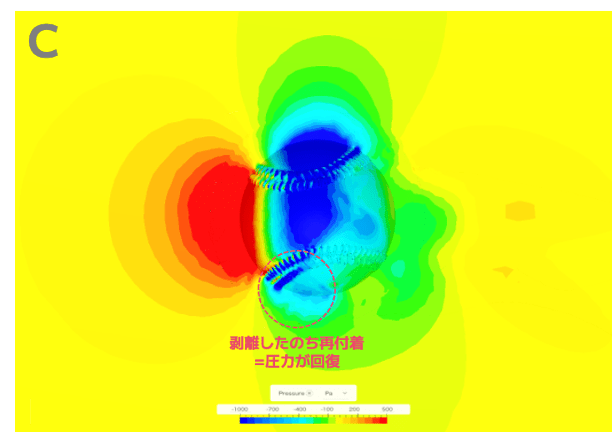
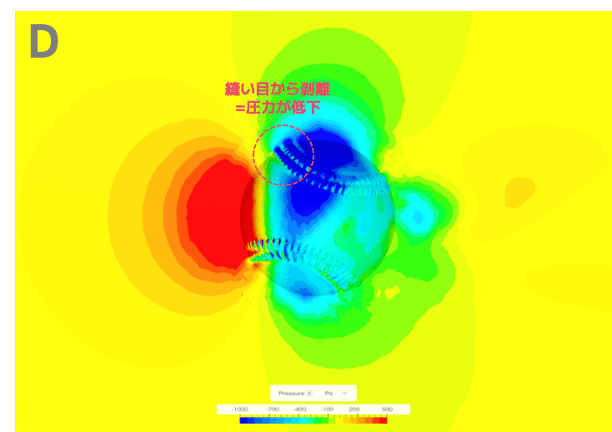
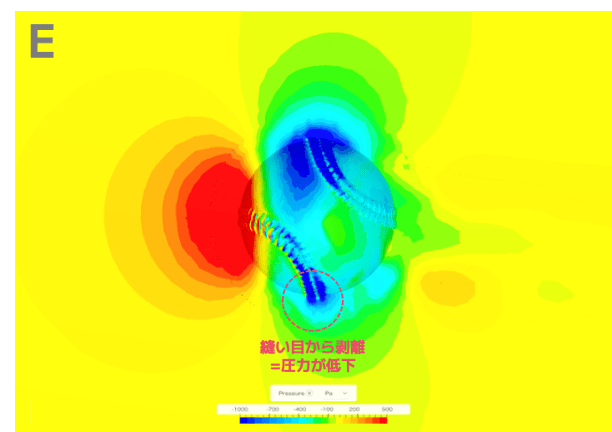
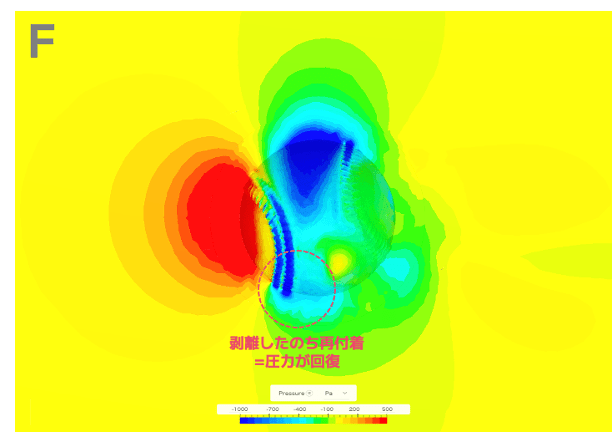
ボールが回転して縫い目の位置が変わることで、ボールの上部と下部では「剥離」と「再付着」という現象が周期的に発生します。
その結果、上下の圧力差も同じ周期で変化し、揚力が揺らいでいるのです。
たった2mm程度の野球ボールの縫い目が、揚力に大きく影響していたことになります。
このように、縫い目が及ぼす揚力への影響を「シームシフトウェイク (SSW: Seam Shifted Wake) 」と呼びます。
近年、純粋なストレートを フォーシーム (4つの縫い目) と呼び、これはボールが1回転する間に4つ縫い目が通過します。
今回確認された1回転で4回の揚力のピークはこれに対応しており、フォーシーム特有のシームシフトウェイクによって生じたものでした。
さらに、ボールの向きを調整することで、1回転する間に通過する縫い目を2つにし、このシームシフトウェイクを意図的に利用して変化させる球種が ツーシーム です。このツーシーム特有の流れと変化についても、以下の記事で詳しく掘り下げています。
4. まとめ: 野球のストレートのノビを生む空気力学の正体 = マグヌス効果
ストレートという一見シンプルな現象の裏には、実は奥深い流体力学の世界が広がっています。
マグヌス効果は、野球ボールにかかる重力にも匹敵するほどの力を生み出し、まさにボールを「ホップ」させます。
さらに、わずか2mmの縫い目がシームシフトウェイクとして働き、揚力の変動にも大きく影響していました。
流体力学の視点で見ても、野球ボールに働く揚力は強すぎず弱すぎず、ゲームとしての面白さを引き立てる絶妙なバランスの上に成り立っていることが分かります。