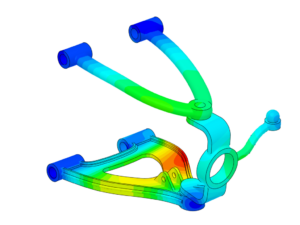
固体力学の分野では、構造解析とは、ある荷重条件下における構造物の応答とその挙動を解析することを指します。
多くの場合、設計が「荷重に耐えられるのか、それとも壊れるのか?」を判断するのが一番の目的です。
構造解析の基本概念
応力とひずみ、材料の挙動
応力とひずみは、構造解析において本当に重要な2つの量です。
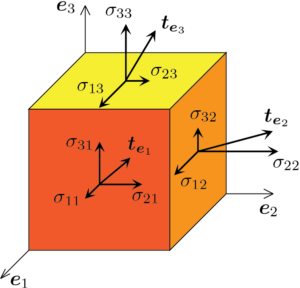
固体では、応力(\(\sigma\))は外部からの荷重に対抗する材料内部の力(F)と定義され、任意の断面(A)で定義できます:
$$\sigma = \frac{F}{A}$$
荷重を受けた固体は変形します。ひずみ (\(\epsilon\)) は、応力下の材料の相対的な変形を定量化する無次元量です。ひずみは次の式で表されます:
$$\epsilon = \frac{\Delta L}{L}$$
ここで、Lは固体の変形前の長さ、\( \Delta L \)は変形量です。
特定の部材で生じる応力とひずみを求めることが、構造解析の主な目的です。しかし、これらの値の他にも同じく重要な量や検討項目があります。代表的な例としては、固有振動数とモード形状、振動応答、座屈、破壊/亀裂伝播、材料疲労などがあります。
応力とひずみの関係は次式で表されます。
$$\epsilon = \frac{\sigma}{E}$$
ここで、E は弾性率、弾性係数、または単にヤング率として知られる特性材料定数です。この係数はイギリスの科学者 Thomas Young にちなんで名付けられました。
ヤング率は、線形弾性固体材料の力学的特性を表す値であり、材料の剛性を定量化します。ヤング率は多くの場合、圧力/応力の単位(Pa)で表されます。
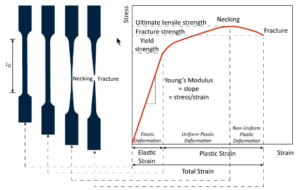
材料について言えば、応力-ひずみ曲線についても触れておきましょう。構造部材として、最も一般的に使用される材料は延性材料です。延性材料でできた部品は、破壊する前に大きなひずみに耐えることができます。図1に延性材料の典型的な応力-ひずみ曲線を示します。
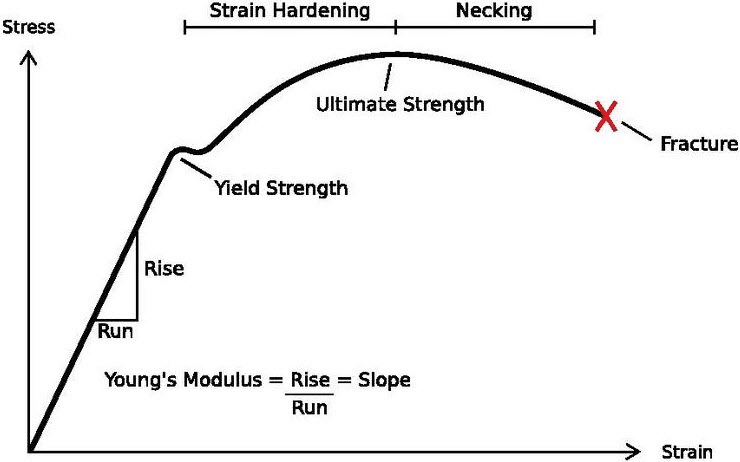
図1: 延性材料の応力-ひずみ曲線[1]
応力-ひずみ曲線は材料それぞれに固有であり、通常は材料試験によって調べられます。例えば、引張試験、圧縮試験、曲げ試験などです。応力-ひずみ曲線は、エンジニアや設計者が材料の強度や破損リスクを知るにあたって重要なものです。
応力とひずみ、そして材料の種類に基づく様々な応力-ひずみ関係についてもっと知りたいですか? 応力-ひずみ曲線に関する記事をお読みください。
許容応力と安全率
部品や構造物の設計プロセスにおいて、構造解析者は、設計が指定された耐用年数の間に生じるであろう、あらゆる荷重に耐えられることを検証します。材料特性とそれに伴う応力-ひずみ特性曲線はこのプロセスに大きく関わります。材料強度に関しては、主に着目するのが以下の二つの値です:
- 材料が非可逆な永久変形(塑性変形)を生じる限界応力とは? ➡ 降伏応力・降伏点
- 材料が破壊するまでに受けることのできる最大応力(材料強度)とは? ➡ 引張強さ
設計者は、発生する応力が使用している材料の引張強さや降伏点を決して超えないように設計します。このとき、最大許容応力はこの2つの限界値よりもいくらか低くする必要があります。その理由は、不確定要素や予想外の極端に大きな荷重が生じた場合を考慮するためです。この余裕度を考えるときに用いられるのが安全率です。
構造解析は、破損を防ぎたい製品を設計する際に、意図した荷重条件だけでなく通常とは異なるシチュエーションの荷重状態で再現して安全率を確認し、十分な安全率を確保するのに役立ちます。
$$安全率=\frac{\text{最大許容応力}}{\text{生じる最大応力}}$$
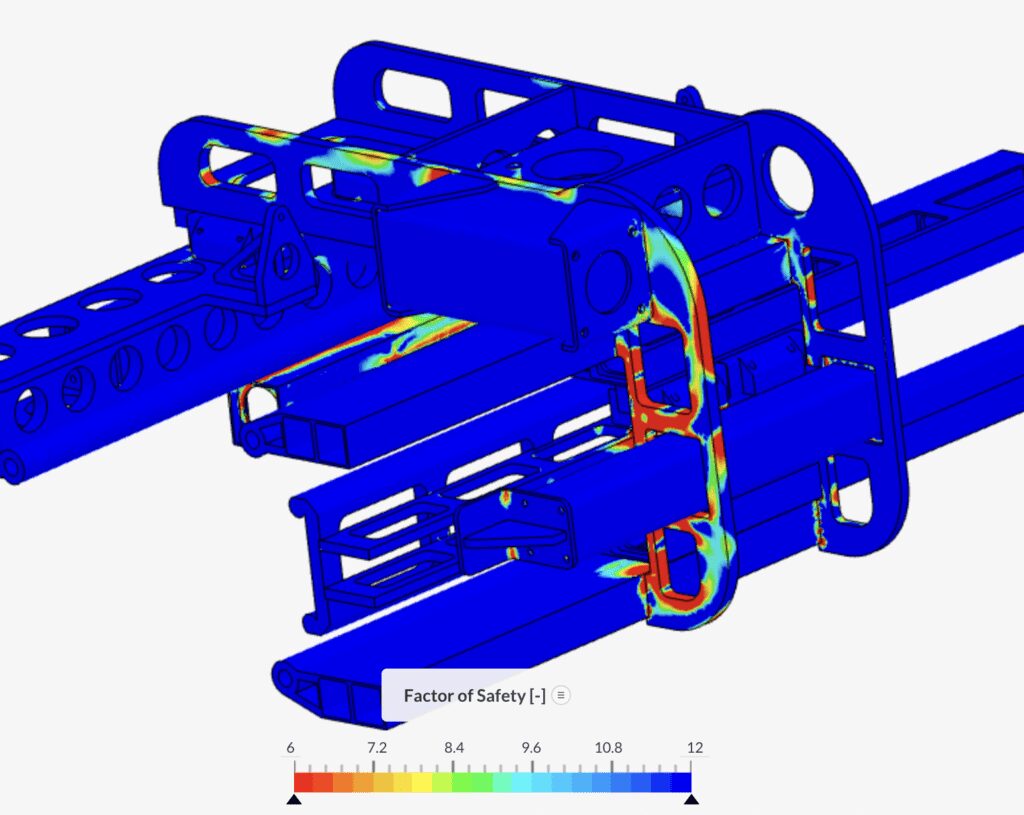
図2: 構造解析で得られた応力から安全率を算出して可視化した様子
構造計算の手法
単純な静定問題の場合、荷重と応力の評価に重要な反力と内力は静力学の考えを用いて計算できます。この場合、未知数の数は一般的に力のつり合いを保つための方程式の数に等しいため、簡単に解けます。これが最も単純な構造計算と言えます。
しかし、未知数の数がつり合い式の数を超える場合もあります。 例えば、先端がピン支持された片持ち梁が該当します。このような不静定問題はどうすれば解けるでしょうか。
仮想仕事の原理、エネルギー法、マトリックス法
構造計算の手法には主に3つの方法があります:
- 仮想仕事の原理:
仮想仕事の原理に基づく解法は、最も強力な手法の1つです。静的に不確定な問題の解析に有効で、線形弾性材料の範囲を超えて考慮することができます。 - エネルギー法:
ひずみエネルギーに基づく方法はより一般的で、複雑な問題の推定解が得られます。この方法は、厳密解が存在しないか、または得ることが困難な場合に特に有用です。 - マトリックス法:
コンピュータと数値計算の進歩により、コンピュータベースの手法が開発されました。Flexibility法とStiffness法はこのカテゴリーに属します。
仮想仕事の原理に基づく方法とひずみエネルギーに基づく方法は、問題によっては手作業で解くことができ、一般に単一の部品といった小規模で単純な系に適しています。マトリックス法は、より大きなアセンブリを解析する必要がある現代の構造設計において非常に有用です。マトリックス法を発展させより大規模な問題に適用するフレームワークが有限要素法(FEM)と言えます。
FEMは、現実のモデルを表す連続体構造に特に適しています。
詳細は有限要素解析についての記事をお読みください。FEMが実用的な工学問題でどのように機能するかを理解するのに役立ちます。
現代の構造解析
コンピュータの発達に伴い、エンジニアや設計者は、日常業務で構造解析手法をより頻繁に使用するようになりました。専用の FEM や構造解析ソフトウェアを使用することで、コンポーネントやアセンブリレベルでの強度検討を事前に行い、実際に試験を行うプロトタイプの数を減らせます。現在では、コンピュータがすべての数式と未知数のセットを処理します。これにより、エンジニアはスピーディーに計算を行い、設計上の意思決定を迅速に行うことができます。
構造解析の種類
構造解析にはいくつかの種類があります。考える現象・問題に応じて、適した解析手法を利用します。構造解析には、静的な現象を扱うものから、動的な現象を扱うもの、あるいは非線形性を伴う現象を考慮したものまで様々な解析手法があります。
以下の解析タイプの紹介を通して、構造解析のさまざまな例を見てみましょう。
SimScaleでは、以下のすべての解析タイプをウェブブラウザで実施できます。ぜひ、アカウントを作成してお試しください。豊富なチュートリアルも用意されています。
静解析
静解析では、1つまたは複数の部材に時間に依存しないで静的に生じる変位・応力・ひずみを計算できます。ベアリングや重力、力といった荷重や制約の結果として生じる結果を計算できます。非線形な解析では、接触摩擦や材料の塑性・超弾性挙動も考慮できます。
この結果によって、エンジニアは対象の部品が望ましくない方法で変形しないかどうかを評価できます。破壊や故障の危険性をもたらすような高応力状態が発生するかどうかを理解するのに役立ちます。静的構造解析の例として、以下のボルトフランジの例をご覧ください。
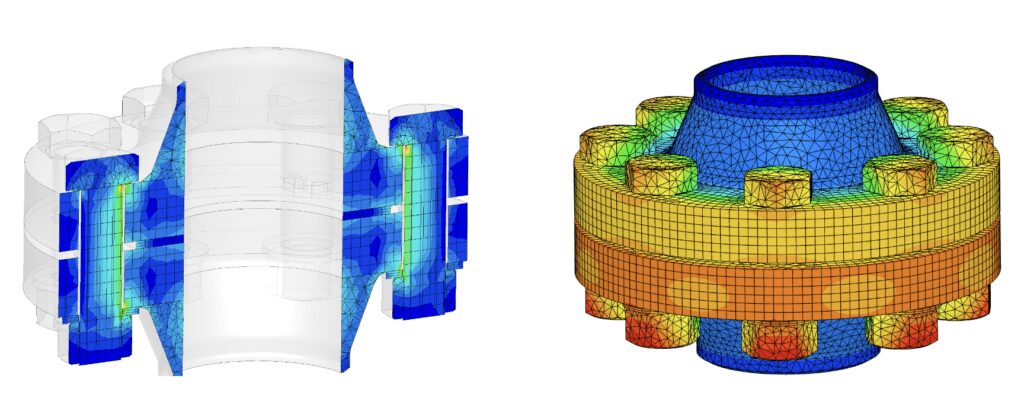
動解析
動解析では、動的に時間変化する変位と応力/ひずみを計算できます。単純な静解析と比較すると、慣性の効果も考慮される点が異なります。
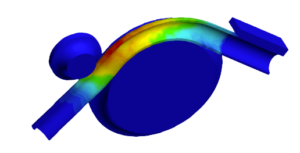
解析の結果、エンジニアは単一のタイムステップだけでなく、時間によって変動する動的性能も解析することができます。静的解析と同様に、最大許容応力と変形に関するモデルの妥当性を経時的に評価することができます。落下試験や衝撃評価は、動的な構造解析が用いられる代表例です。
図4: 衝撃を受けたヘッドセット
熱伝導解析・熱応力解析
伝熱挙動と構造挙動の組み合わせの影響を検討できます。具体的には、熱荷重と構造荷重の組み合わせによって発生する応力を計算する際に役立ちます。熱と構造の計算結果は逐次的に得られます。通常は、まず熱伝導の解析を行い、得られた温度分布をもとに変形挙動、生じる応力を計算します。
SimScaleでは、静的な熱解析から、時刻歴の温度変化・変形を考慮する解析も可能です。
適用例としては、バルブに生じる熱応力や、スパークプラグの熱衝撃が挙げられます。

図5: グローブバルブの熱衝撃
固有値解析・調波数応答解析
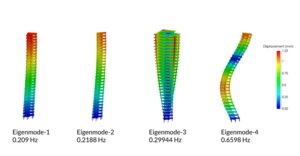
固有値解析(固有振動解析)では、構造物の固有振動数(固有周波数)を計算できます。また、対応する振動モード形状(固有モード)の計算も可能です。結果として得られる周波数と変形モードは、形状と材料特性に依存します。
固有値解析では、構造物の全体的な剛性を評価し、共振につながる可能性のある「危険な」周波数を調べられます。得られる結果は、設計の振動特性を評価する第一歩となります。
固有振動解析は多くの場合、後の周波数応答解析へのステップとなります。周波数応答解析は、定常的な周期的(正弦波)荷重によって励起される固体の応答を計算できます。慣性効果が考慮される動的解析とよく似ていますが、結果が時間依存ではなく周波数依存になるという点で異なります。言い換えれば、周波数応答解析では、定義された周波数スペクトルにわたって振動する力や変位に対する構造物の応答を計算することができます。このような研究では、減衰効果も考慮することができます。
固有モード |
固有周波数 |
| 1.0 | 233.433 |
| 2.0 | 236.206 |
| 3.0 | 251.691 |
| 4.0 | 362.203 |
| 5.0 | 364.132 |
図7: 加振下でのEVバッテリーモジュールのケーシング応答
参考
- “Wikimedia commons: Stress Strain Ductile Material.”
- T.H.G. Megson, Aircraft Structures for Engineering Students
構造解析に関する記事
有限要素法(Finite Element Method | FEM)とは
有限要素解析(Finite Element Analysis | FEA)とは、有限要素法(Finite Element Method | FEM)と呼ばれる数値解析技術を用いて、任意の物理現象をシミュレーションすること […]
フォンミーゼス応力とは
フォンミーゼス応力とは、与えられた材料が降伏するか破壊するかを決定するために使用される値です。主に金属などの延性材料に用いられます。フォンミーゼス降伏基準は、荷重を受けた材料のフォンミーゼス応力が、単純引張を受けた同じ材 […]
主応力と主ひずみとは
主応力と主ひずみは、構造工学と設計における基本的な概念であり、材料と構造物の評価と解析を支えています。様々な用途の安全性と安定性に不可欠なこれらの用語は、外部荷重を受けた際に材料が受ける内部力と変形を反映しています。これ […]
SimScale製品紹介資料ダウンロード

SimScaleの特徴と計算事例をまとめた資料を用意しております。